22. Расчет диаметра трубопровода, выбор расчетных скоростей потока и примерные численные их значения для капельных жидкостей, газов, паров.

При известном расходе жидкости при средней скорости диаметр трубопровода может быть определен из формулы:

Диаметр трубопровода зависит от скорости протекающей жидкости. С увеличением скорости диаметр уменьшается, следовательно уменьшается его стоимость, но увеличиваются потери напора и затраты на транспортировку.

Оптимальные скорости движения:

• Жидкость вязкая –

• Жидкость невязкая –

• Газ при низком давлении –

• Газ при повышенном давлении –

• Насыщенный пар –

23. Определение гидравлического сопротивления в трубопроводах и аппаратах. Как определяются потери напора на трение при турбулентном движении?

Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения.

где – коэффициент Дарси.

Таблица 5.1 – Коэффициент Дарси в разных режимах течения

Режим течения	Число Рейнольдса	Коэффициент Дарси
Ламинарный
Переходный		-
Турбулентный

24. Приведите и поясните графическую зависимость коэффициента гидравлического трения от критерия Рейнольдса и шероховатости стенки трубопровода при различных режимах течения жидкости.

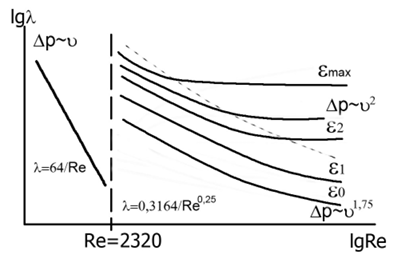
Рисунок 6.1 – Зависимость коэффициента гидравлического трения от критерия Рейнольдса

При ламинарном течении , то есть коэффициент Дарси не зависит от шероховатости труб.

При турбулентном течении , то есть коэффициент Дарси зависит и от числа Рейнольдса и от шероховатости труб.

В автомодельном режиме , то есть коэффициент Дарси не зависит от числа Рейнольдса.

25. Что такое «гидравлическая гладкость» при течении жидкостей по трубопроводам? Каковы условия, в которых она проявляется?

Гидравлическая гладкость – отсутствие влияния шероховатости труб на коэффициент гидравлического трения потока жидкости. Гидравлическая гладкость проявляется при ламинарном режиме течения, а также в некоторой области турбулентного режима, когда толщина вязкого подслоя больше высоты выступов шероховатости.

26. Расчет потери давления в трубопроводах на трение и местные сопротивления. Приведите формулы, необходимые при таком расчете.

– потери давления на трение;

– потери давления на местные сопротивления.

27. Приведите с необходимыми пояснениями расчетную формулу для определения потерь давления (напора) при течении жидкостей через трубопроводы и каналы. От чего зависит величина коэффициента трения?

– потери давления на трение;

– потери давления на местные сопротивления.

– потери напора на трение соответственно;

– потери напора и давления на местные сопротивления соответственно.

Величина коэффициента трения зависит от числа Рейнольдса и шероховатости.

28. Принципы измерения скоростей и расходов жидкостей в трубопроводах, основанные на определении перепада давления.

Принципы измерения скоростей и расходов жидкостей в трубопроводах, основанные на определении перепада давления.

Рисунок 10.1 – Трубка Пито-Прандтля

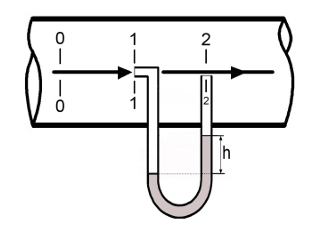Т рубки Пито-Прандтля представляют собой две тонкие трубки (пьезометры) диаметром 1-2 мм, расположенные на одном уровне. Одна из трубок (трубка Пито) изогнута под прямым углом, открытым концом направлена в сторону набегающего потока, вторая трубка – прямая, расположена поперек потока. Трубка Пито воспринимает полное давление потока (динамическое и статическое), а вторая (прямая) трубка – только статическое. Разность этих двух давлений эквивалентна динамическому давлению потока в том месте сечения, где находится трубка Пито:

где ρ – плотность среды в трубопроводе; – локальная скорость потока в точке измерения.

Возникающая разность давлений определяется дифференциальным манометром:

где – плотность жидкости в манометре, – высота столба манометрической жидкости.

Таким образом, локальную скорость определяют по соотношению:

Рисунок 10.2 – Диафрагма

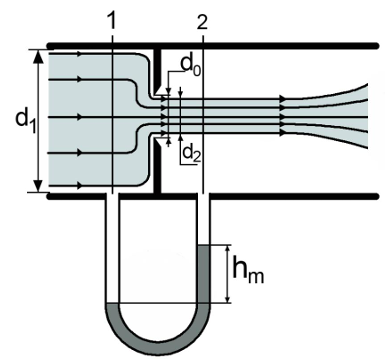Д иафрагма представляет собой тонкий металлический диск с круглым отверстием посередине, размещаемый внутри трубы, поперек потока. Диаметр отверстия диафрагмы значительно меньше диаметра трубы, на которой устанавливается диафрагма. За диафрагмой струя жидкости продолжает сжиматься, поэтому на некотором расстоянии за диафрагмой при максимальном сжатии потока диаметр струи становится равным , причем . К сечениям 1 и 2 присоединен U-образный дифманометр. Найдем разность давлений в сечениях 1 и 2, используя уравнение Бернулли:

С учетом того, что , уравнение можно записать следующим образом:

Перепад давления в трубопроводе через показания U-образного дифманометра:

Также из условия постоянства объемных расходов капельных жидкостей следует:

Откуда:

Скорость жидкости в отверстии диафрагмы определяет значение скорости .

где – коэффициент расхода диафрагмы.

Тогда объемный расход жидкости в отверстии диафрагмы и в трубе:

Можно также использовать формулу .

С целью снижения гидравлических потерь на острых кромках диафрагмы вместо нее для определения расходов жидкостей могут устанавливаться сопла с гладким входом.

Р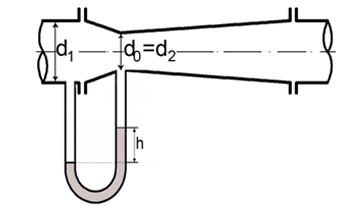 асходомерная труба Вентури устанавливается в случае, если нежелательны большие потери напора в суживающим устройстве. Основной недостаток трубы Вентури по сравнению с диафрагмой - громоздкость.

Рисунок 10.3 – Расходомерная труба Вентури

Можно также использовать формулу где – коэффициент расхода трубы Вентури.