Вывод уравнения для расчета коэффициента гидравлического трения при ламинарном движении жидкости в трубе круглого поперечного сечения.
Расход вязкой несжимаемой жидкости при ламинарном течении в прямой круглой трубе определяется уравнением Пуазейля:
Определим расход
жидкости в прямой трубе круглого сечения.
Запишем элементарный расход жидкости
через кольцевой канал площадью
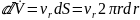
Проинтегрируем, учитывая, что
Получим уравнение Пуазейля
Перепад давления P из этого уравнения:
Из уравнения
Бернулли:
где
– потери на трение, выразим потери
на трение для горизонтальной трубы
постоянного сечения.
Подставим в это
уравнение
из уравнения (1), с учетом, что
С учетом того, что
,
обозначим величину
– коэффициент гидравлического
сопротивления или коэффициент Дарси.
Вывод уравнения Бернулли для идеальной жидкости. Приведите примеры практического использования этого уравнения.
Рассмотрим стационарное движение физически бесконечно малого объема идеальной жидкости по линии тока, совпадающей с траекторией движения этой жидкой частицы. В проекциях на оси координат это движение описывается системой уравнений Эйлера:
Умножим правые и левые части системы уравнений (14.1) на соответствующие проекции элементарного пути, пройденного частицей: :
С учетом, что , просуммировав левые и правые части системы уравнений (14.2) получим:
В случае несжимаемой жидкости
Откуда уравнение Бернулли или основное уравнение гидростатики имеет вид:
Чаще это уравнение записывают в таком виде:
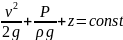
Физический смысл слагаемых
– кинетическая энергия (динамический напор)
– потенциальная энергия (пьезометрический напор)
– положение точки на линии тока (геометрический напор)
– величина, меняющаяся для различных линий тока
Практические приложения
Измерение расходов жидкостей и газов дроссельными устройствами.
Расчет истечения жидкости из отверстия в днище сосуда.
Вывод уравнения Бернулли для идеальной жидкости. Опишите особенности движения реальной жидкости. Приведите вид уравнения Бернулли для реальной жидкости. Каков его энергетический смысл?
Рассмотрим стационарное движение физически бесконечно малого объема идеальной жидкости по линии тока, совпадающей с траекторией движения этой жидкой частицы. В проекциях на оси координат это движение описывается системой уравнений Эйлера:
Умножим правые и левые части системы уравнений (15.1) на соответствующие проекции элементарного пути, пройденного частицей: :
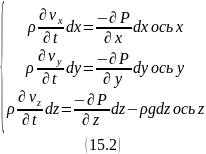
С учетом, что , просуммировав левые и правые части системы уравнений (15.2) получим:
В случае несжимаемой жидкости
Откуда уравнение Бернулли или основное уравнение гидростатики имеет вид:
Чаще это уравнение записывают в таком виде:
Физический смысл слагаемых
– кинетическая энергия (динамический напор)
– потенциальная энергия (пьезометрический напор)
– положение точки на линии тока (геометрический напор)
– величина, меняющаяся для различных линий тока
Практические приложения
Измерение расходов жидкостей и газов дроссельными устройствами.
Расчет истечения жидкости из отверстия в днище сосуда.
При течении реальных жидкостей действуют силы межмолекулярного взаимодействия. Уравнение Бернулли принимает вид:
где,
и
– потери давления и напора соответственно,
которые возникают из-за увеличения
внутренней тепловой энергии.
Вывод уравнения, представляющего энергетический баланс движения идеальной жидкости. Каков физический смысл слагаемых этого уравнения?
Рассмотрим стационарное движение физически бесконечно малого объема идеальной жидкости по линии тока, совпадающей с траекторией движения этой жидкой частицы. В проекциях на оси координат это движение описывается системой уравнений Эйлера:
Умножим правые и левые части системы уравнений (15.1) на соответствующие проекции элементарного пути, пройденного частицей: :
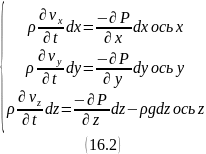
С учетом, что , просуммировав левые и правые части системы уравнений (16.2) получим:
В случае несжимаемой жидкости
Откуда уравнение Бернулли или основное уравнение гидростатики имеет вид:
Чаще это уравнение записывают в таком виде:
Физический смысл слагаемых
– кинетическая энергия (динамический напор)
– потенциальная энергия (пьезометрический напор)
– положение точки на линии тока (геометрический напор)
– величина, меняющаяся для различных линий тока