55. Вывод уравнения для расчета средней движущей силы процесса теплопередачи при переменных температурах теплоносителей вдоль поверхности теплообмена при противотоке теплоносителей.

Рассмотрим теплообмен через плоскую стенку, где с одной стороны стенки горячий теплоноситель с расходом и теплоемкостью , а с другой стороны стенки- холодный теплоноситель с расходом и теплоемкостью .

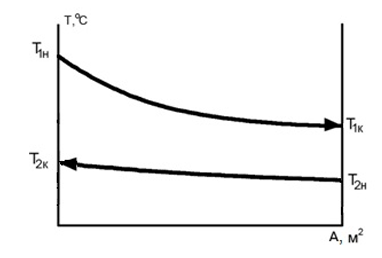
Рисунок 11.1 – К выводу уравнения движущей силы теплопередачи

Примем допущения:

• Процесс теплообмена стационарный;

• Теплоемкости теплоносителей и постоянны;

• Коэффициент теплопередачи не изменяется вдоль всей поверхности теплообмена;

• Теплоносители движутся в поршневом режиме, т.е. их движение описывается моделью идеального вытеснения;

• Потери теплоты отсутствуют.

На графике изображен профиль температур горячего 1 и холодного 2 теплоносителей вдоль поверхности теплообмена; - элементарная поверхность теплообмена .

Запишем уравнение теплового баланса для элементарной поверхности ;

Получим

Выразим из основного уравнения теплопередачи, считая, что перенос теплоты на элементарном участке происходит при постоянных температурах теплоносителей.

Проинтегрируем:

Получим:

Запишем уравнение теплового баланса для всего теплообменника:

отсюда получим:

– большая и меньшая, если сравнивать численно, разность температур на концах теплообменника.

Тогда средняя движущая сила:

Если , то с достаточной для инженерных расчетов точностью можно определить как

56. Вывод уравнения для расчета движущей силы теплопередачи при переменных температурах теплоносителей вдоль поверхности теплообмена.

Рассмотрим теплообмен через плоскую стенку, где с одной стороны стенки горячий теплоноситель с расходом и теплоемкостью , а с другой стороны стенки- холодный теплоноситель с расходом и теплоемкостью .

Примем допущения.

• Процесс теплообмена стационарный;

• Теплоемкости теплоносителей и постоянны;

• Коэффициент теплопередачи не изменяется вдоль всей поверхности теплообмена;

• Теплоносители движутся в поршневом режиме, т.е. их движение описывается моделью идеального вытеснения;

• Потери теплоты отсутствуют.

На изображен профиль температур горячего 1 и холодного 2 теплоносителей вдоль поверхности теплообмена; - элементарная поверхность 3 4 теплообмена .

Запишем уравнение теплового баланса для элементарной поверхности ;

Получим

Выразим из основного уравнения теплопередачи, считая, что перенос теплоты на элементарном участке происходит при постоянных температурах теплоносителей.

Проинтегрируем:

Получим:

Запишем уравнение теплового баланса для всего теплообменника:

отсюда получим:

- большая и меньшая, если сравнивать численно, разность температур на концах теплообменника.

тогда:

Если , то с достаточной для инженерных расчетов точностью можно определить как

4. Вопросы без вывода

1. Механизмы переноса энергии в форме теплоты в жидкостях и газах. Феноменологический закон переноса энергии Фурье.

Перенос теплоты осуществляется тремя способами (механизмами):

1. Теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов). В чистом виде теплопроводность наблюдается только в неподвижных средах - твердых телах.

2. Перенос теплоты конвекцией. Такой способ возможен только в подвижных средах, т.е. в жидкостях и газах. Теплота переносится макрообъемами среды при их перемещении под действием каких-либо сил. Конвекция всегда сопровождается теплопроводностью.

3. Перенос теплоты излучением. В этом случае энергия переносится в виде электромагнитных волн через оптически прозрачную среду. При этом внутренняя энергия переходит в лучистую, которая впоследствии поглощается другими телами. В чистом виде такой механизм наблюдается в вакууме. Пример – Солнце и планеты.

Таблица 1.1 – Механизмы переноса в различных средах

Механизм переноса Среда	Теплопроводность	Конвекция	Излучение
Твердые тела
Жидкости
Газы

При описании процессов теплообмена, происходящих в промышленном оборудовании, различают два понятия:

1. Теплоотдача – перенос теплоты в пределах одной фазы от границы раздела или от стенки к жидкому (газообразному) теплоносителю (или наоборот).

2. Теплопередача – перенос теплоты от горячего теплоносителя к холодному через границу раздела или через разделяющую теплоносители теплопередающую твердую стенку.

Температурный градиент – вектор, направленный в сторону максимального возрастания температуры, являющийся производной по нормали к изотермической поверхности.

где – единичный вектор, «нормальный» к поверхности.

Фурье экспериментально установил, что при переносе теплоты теплопроводностью удельный тепловой поток пропорционален градиенту температур, т.е.:

где – коэффициент теплопроводности . Знак указывает, что теплота переносится в сторону уменьшения температуры.

Полученное уравнение называется феноменологическим законом теплопроводности Фурье.