
Саляхов ИВТ-329Б ЛР№1
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Уфимский университет науки и технологий»
Лабораторная работа №1
по дисциплине «Теория принятия решений»
«Модели принятия решений в условиях риска»
Вариант №2
Выполнил: студент гр. ИВТ-329Б
Саляхов А.Ф.
Проверил доц. каф. ТК
Насыров Р.В.
Уфа-2023
Цель работы: смоделировать систему выбора оптимального решения в соответствии с заданной целевой функцией.
1.Теоретическая часть.
Оптимистический критерий (критерий азартного игрока):
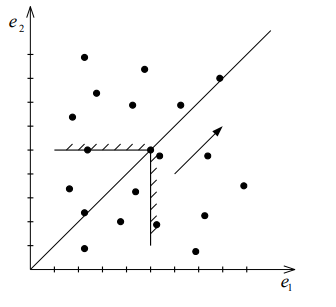
К матрице полезностей дописывается дополнительный столбец. Его элементы определяются как самые лучшие (наибольшие) возможные конечные экономические результаты при соответствующем решении (по строкам матрицы). Затем из всех элементов такого дополнительного столбца находится самый лучший (наибольший). По такому элементу и определяют оптимальное решение: им будет решение соответствующей строки матрицы полезностей.
Геометрическое представление:
Критерий Гурвица:
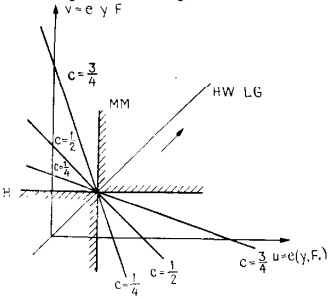
Критерий Гурвица. Правило выбора, согласно этому критерию, можно интерпретировать так. Матрица решений дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки:
![]()
Выбираются те варианты Ei0, в строках которых стоят наибольшие элементы eir этого столбца.
Для c 1 критерий Гурвица превращается в минимаксный критерий. Для c 0 он превращается в критерий азартного игрока. Таким образом, путем изменения данного параметра осуществляется варьирование между этими двумя крайними точками исходя из значения допустимого риска.
Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:
- о вероятностях появления состояний ничего не известно;
- с появлением состояний необходимо считаться;
- реализуется лишь малое количество решений;
- допускается некоторый риск.
Геометрическое представление:
2. Текст программы
#include <stdafx.h>
#include <iostream>
#include <cstdlib>
#include <iomanip>
#include <Windows.h>
#include <conio.h>
#include <time.h>
using namespace std;
double optimistic(double matrix[][14], double maxi[], int rows, int cols) {
double maxmax = 0;
int resh = 0;
cout << "\tСтолбец максимальных значений:" << endl;
for (int i = 0; i < rows; i++) {
double max = 0;
for (int j = 0; j < cols; j++) {
if (matrix[i][j] > max) {
max = matrix[i][j];
maxi[i] = max;
}
}
cout << "\t" << maxi[i] << endl;
}
for (int i = 0; i < rows; i++){
maxmax = maxi[i];
for ( i = 0; i < rows; i++) {
if (maxi[i] > maxmax){
maxmax = maxi[i];
resh = i;
}
}
}
cout << "\n\t" << maxmax << endl;
cout << "\n";
return resh;
}
double Gurwitz(double matrix[][14], int rows, int cols, double alpha) {
double maxMin = 0;
int resh = 0;
cout << "\tСтолбец средних взвешенных:" << endl;
for (int i = 0; i < rows; i++) {
double min = 100;
double max = 0;
for (int j = 0; j < cols; j++) {
if (matrix[i][j] < min) {
min = matrix[i][j];
}
if (matrix[i][j] > max) {
max = matrix[i][j];
}
}
double z = alpha * min + (1.0 - alpha) * max;
cout << "\t" << z << endl;
if ( z > maxMin) {
resh = i;
maxMin = z;
}
}
cout << "\n\t" << maxMin << endl;
cout << "\n";
return resh;
}
int main() {
SetConsoleCP(1251);
SetConsoleOutputCP(1251);
const int rows = 10;
const int cols = 14;
double alpha = 0.3;
double matrix[rows][cols];
double maxi[rows];
cout << endl;
srand(time(NULL));
for (int i = 0; i < rows; i++) {
cout << "\t";
for (int j = 0; j < cols; j++) {
matrix[i][j] = rand() % 100 + 1;
cout << setw(4) << matrix[i][j] << " ";
}
cout << endl;
}
int result1 = optimistic(matrix, maxi, rows, cols);
int result2 = Gurwitz(matrix, rows, cols, alpha);
cout << "\n\tОптимистический критерий: \n\t\tСтрока: " << result1+1 << endl << "\t\t\t";
for (int i = 0; i < cols; i++){
cout << setw(4) << matrix[result1][i];
}
cout << "\n\tКритерий Гурвица: \n\t\tСтрока:" << result2+1 << endl << "\t\t\t";
for (int i = 0; i < cols; i++){
cout << setw(4) << matrix[result2][i];
}
_getch();
return 0;
}
3. Тестирование
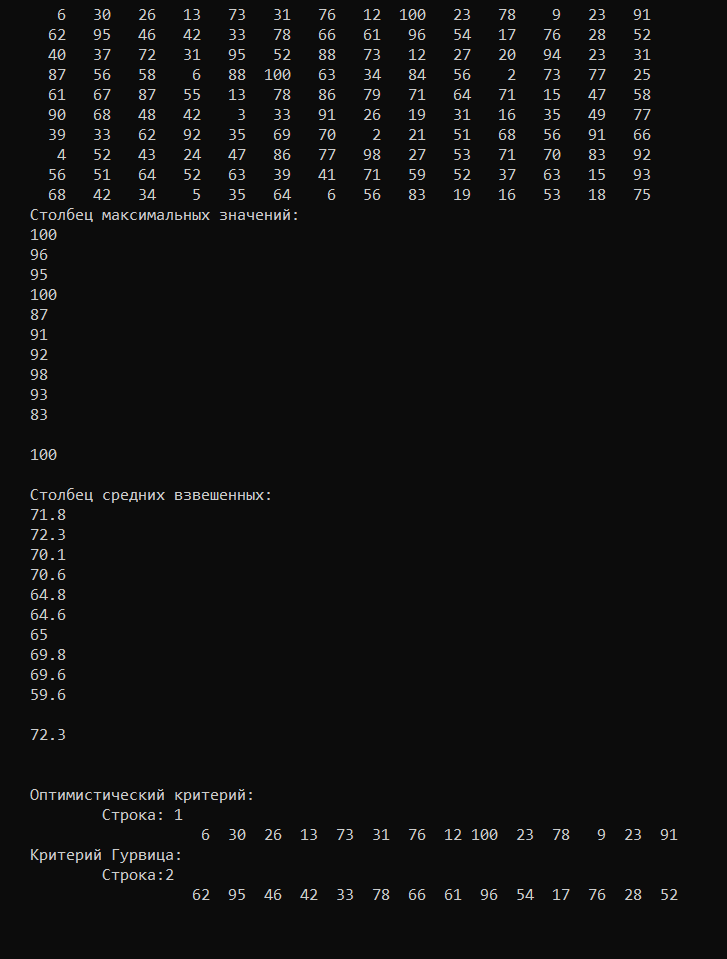
Тест №1:
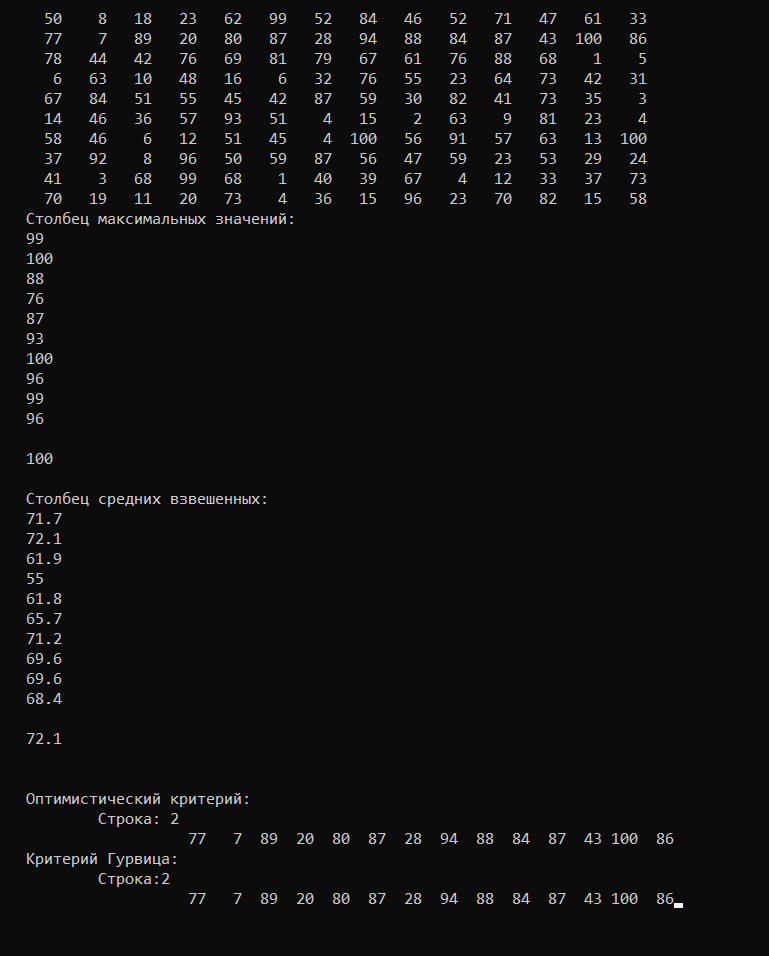
Тест №2:
Тест №3:
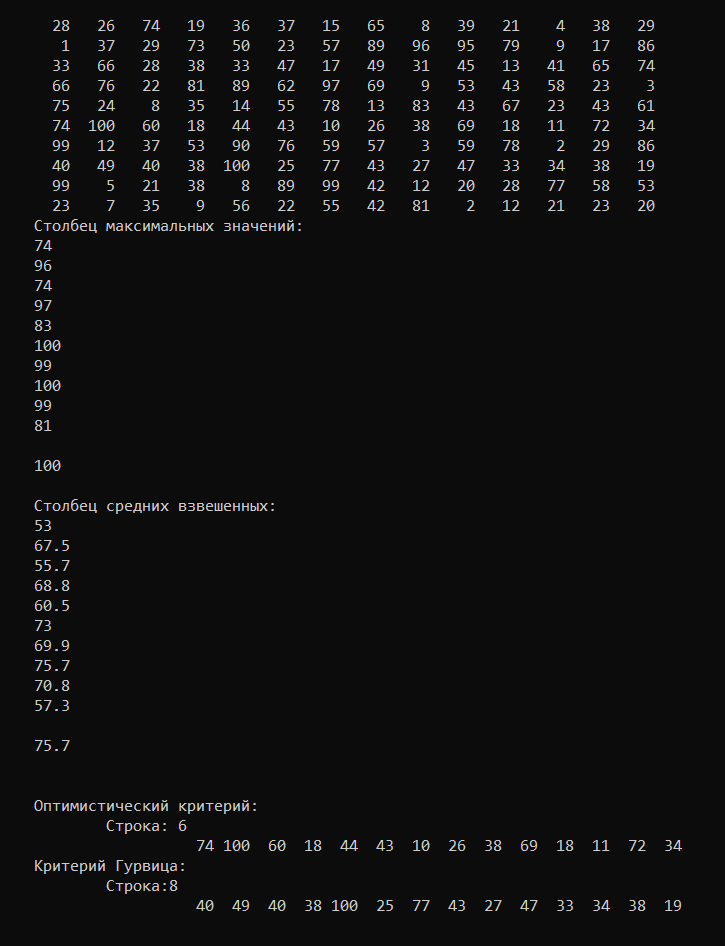
Оптимистический критерий: матрица дополняется столбцом, содержащий максимальные значения для каждой строки. Из этого столбца выбирается максимальное значение.
Критерий Гурвица: матрица дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки. Из этого столбца выбирается максимальное значение.
Вывод: Оптимистический критерий характеризуется крайней оптимистической позицией отношения ЛПР к неопределённости экономического результата, т.е. позицией “азартного игрока”, уверенного в том, что ему должно повезти, и поэтому склонного к самым рискованным выборам. В рамках такого подхода при сравнении альтернативных решений за основу принимаются их самые благоприятные результаты среди возможных ситуаций. Выбирается решение, применительно к которому самый благоприятный результат будет наибольшим.
Критерий Гурвица характеризуется, взвешенной позицией “пессимизма-оптимизма”, отражающей отношение ЛПР к неопределённости экономического результата. В рамках такого подхода при сравнении альтернатив за основу принимаются самый неблагоприятный и самый благоприятный конечные экономические результаты дохода / прибыли.
Эти “крайние” (самый благоприятный и самый неблагоприятный) результаты учитываются с определёнными “весами”, выбираемыми непосредственно самим ЛПР. При таком подходе их синтез будет характеризовать приемлемый для ЛПР баланс между готовностью рисковать и склонностью к осторожным решениям. Выбирается решение, применительно к которому такая “взвешенная” оценка будет наиболее приемлемой (наибольшей, т.к. она относится к показателю дохода).
