Министерство науки и образования Российской Федерации

Федеральное государственное бюджетное общеобразовательное учреждение высшего образования

«Уфимский университет науки и технологий»

Кафедра АСУ

Лабораторная работа №3

По дисциплине «Проектирование и эксплуатация АСУТП»

«Настройка ПИД-регулятора»

Выполнил:

Ст. гр. ИВТ-329Б Саляхов А.Ф.

Номер з.к.: 17130458

Проверил:

Доцент каф. АСУ Старцев Ю.В.

Уфа 2024

Цель работы: изучение принципов расчета начальных значений параметров ПИД-регулятора. Изучение принципов функционирования и правил ручной настройки параметров ПИД-регулятора на основе правил и на основе нечеткой логики. Использование SCADA-системы TRACE MODE 6 для моделирования замкнутой системы управления с ПИД-регулятором.

Задачи: Расчет начальных значений параметров ПИД-регулятора по методу Зиглера и Никольса. Ручная настройка параметров ПИД-регулятора. Настройка параметров ПИД-регулятора с использованием нечеткой логики. Моделирование замкнутой системы управления с ПИД-регулятором с использованием SCADA-системы TRACE MODE 6.

Теоретическая часть:

Впервые методику расчета параметров ПИД-регуляторы предложили Зиглер и Никольс в 1942 г. Эта методика очень проста и дает не очень хоро­шие результаты. Тем не менее она до сих пор часто используется на практике, хотя с тех пор появилось множество более точных методов. Фактически было предложено два метода настройки ПИД-регуляторов. Один из них основан на параметрах отклика объекта на единичный скачок, второй — на частотных характеристиках объекта управления.

Для расчета параметров ПИД-регулятора по отклику объекта на единичный скачок используется представление объекта в виде инерционного звена первого порядка с запаздыванием. Передаточная функция такого звена имеет вид:

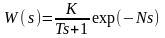, (1)

где s – оператор Лапласа,

K – коэффициент передачи,

T – постоянная времени,

N – запаздывание.

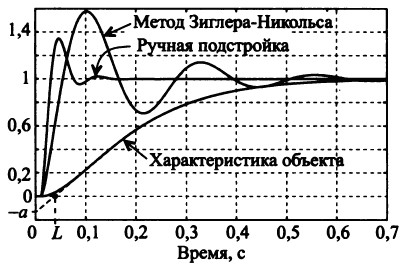
Рис. 1. Переходные характеристики объекта управления и замкнутой системы с ПИД-регулятором на единичное воздействие

Ручная настройка параметров ПИД-регулятора выполняется на основе правил. Эти правила получены из опыта, теоретического анализа и численных экспериментов. Применение правил возможно только после предварительной настройки регулятора по формулам (в частности, по методу Зиглера-Никольса). Попытки настроить регулятор без начального приближенного расчета коэффициентов могут быть безуспешными.

Самый простой способ ручной настройки ПИД-регуляторов выглядит следующим образом.

Принимаем Kи = Kд = 0. Для Kп принимаем такое начальное значение, при котором в замкнутой системе отсутствуют автоколебания. Это может быть значение, полученное по методу Зиглера-Никольса, если при нем нет автоколебаний.

1. Увeличиваем Kп до такого критического значения Kпкр, пока в системе не начнутся автоколебания.

2. Фиксируем принятое значение Kп = Kпкр/2, в дальнейшем его не изменяем. Принимаем Kд = 0, увeличиваем Kи до такого критического значения Kикр, пока в системе не начнутся автоколебания.

3. Фиксируем принятые значения Kп = Kпкр/2, Kи = Kикр/2, в дальнейшем их не изменяем. Увeличиваем Kд до такого критического значения Kдкр, пока в системе не начнутся автоколебания.

4. Фиксируем принятые значения Kп = Kпкр/2, Kи = Kикр/2, Kд = Kдкр/2. Считаем настройку ПИД-регулятора завершенной.

Нечеткая логика в ПИД-регуляторах используется преимущественно двумя путями:

• для построения самого регулятора;

• для организации подстройки коэффициентов ПИД-регулятора.

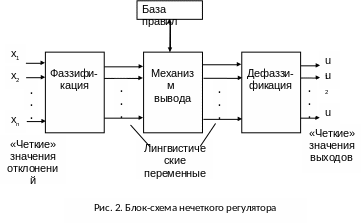
Блок-схема нечеткого регулятора в общем случае принимает вид, изображенный на рис. 3.3.

Как видно из данной схемы, формирование управляющих воздействий включает в себя следующие этапы:

а) получение отклонений управляемых координат и скоростей их изменения - ;

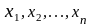б) «фаззификация» этих данных, т.е. преобразование полученных значений к нечеткому виду, в форме лингвистических переменных;

в) определение нечетких (качественных) значений выходных переменных (управлений) в виде функций их принадлежности соответствующим нечетким подмножествам на основе заранее сформулированных правил логического вывода, записанных в базе правил;

г) «дефаззификация», т.е вычисление реальных числовых значений выходов u₁ , u₂ , … , u_m , используемых для управления объектом.

Помимо варианта «чистого» использования нечеткого управления, существуют и другие варианты построения систем управления с нечеткими регуляторами. Так, в классической теории регулирования широкое распространение получило использование ПИД-регулятора, выходной сигнал которого формулируется по формуле:

, (2)

где параметры K_п, K_и, K_д характеризуют удельный вес соответственно пропорциональной, интегральной и дифференциальной составляющей и должны выбираться исходя из заданных показателей качества регулирования (рис. 3.4):

• максимум ошибки регулирования e_max,

• момент времени T_max, при котором ошибка достигает этого максимума,

• декремент затухания d: отношение первого максимума ошибки регулирования a ко второму b,

• статическая ошибка e₀ относительно уставки r(t),

• время установления Т_e с заданной погрешностью e_s,

• перерегулирование σ: величина a [%],

• время нарастания T_r — интервал времени, в течение которого выходная переменная нарастает от 10% до 90 % от своего установившегося значения,

• период затухающих колебании T_p.

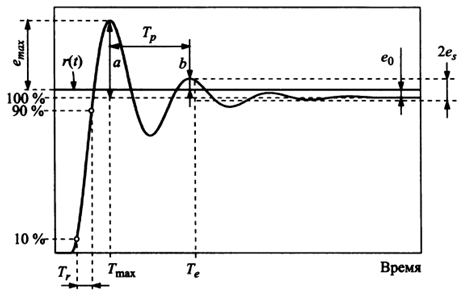
Рис. 3. Критерии качества регулирования во временной области