3.2.3. Поиск оптимальной траектории.

Для решения задачи планирования траектории применим принцип динамического программирования Р. Беллмана, заключающийся в пошаговой процедуре нахождения оптимальной траектории, начиная с конечной точки. Эта процедура описывается рекуррентным соотношением

, (7)

где

. (8)

Согласно принципу оптимальности Р. Беллмана и рекуррентному соотношению (7), на каждом j+1-м шаге нахождения оптимальной траектории должно быть выбрано такое управление U, которое доставляет минимум сумме , в которую входит значение функционала , уже вычисленное на j-м шаге. При этом в качестве начального значения для функционала следует принять его величину в конечной точке, равную, например, нулю.

Соответственно с уравнением (7) каждой клетке дискретного рабочего пространства можно приписать значение функционала J, и это значение будет соответствовать длине оптимальной траектории, переводящей МО из этой точки в конечную точку с учетом штрафов за преодоление перепадов высот. Соответствующие значения функционала будут являться элементами матрицы L (той же размерности, что и матрица M), отображающей дискретную рабочую область. Процедуру вычисления элементов матрицы L нужно начинать с конечной точки траектории. Окрестность конечной точки представлена на рис. 2.

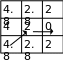
Рис. 2. Значения функционала - элементов матрицы L в окрестности конечной точки при Δx = 2

Каждый элемент матрицы L, соседний с конечной точкой, при отсутствии штрафа вблизи конечной точки принимает значение, равное расстоянию до конечной точки. Далее следует повторить процедуру вычисления элементов матрицы L, рассматривая каждый элемент окрестности конечной точки как промежуточную конечную точку.

Процедура вычисления повторяется аналогичным образом для клеток, находящихся на расстоянии 2 клеток от конечной точки, затем на расстоянии 3 клеток и т.д. Заполнив таким образом всю матрицу L, получим кратчайший путь от начальной точки к конечной, двигаясь из текущей клетки в такую из соседних, значение функционала в которой минимально. Например, на рисунке 2 стрелками показана оптимальная траектория из левой нижней клетки в клетку конечной точки. Отсутствие локальных минимумов гарантируется тем, что в каждом внешнем слое клеток не могут находиться значения функционала, меньшие или равные значениям функционала во внутреннем слое клеток.

Клетки, соответствующие препятствиям, помечаются значениями функционала, заведомо большими, чем любое значение для клетки свободного пространства.

Описание рабочего пространства с перепадами высот и непреодолимыми препятствиями, задание начальной и конечной ячеек рабочего пространства, реализация поиска оптимальной траектории, формирование управляющих воздействий производится в базе данных Microsoft Access.

3.2.4. Модель движения мо в рабочем пространстве.

Использована упрощенная модель динамики МО:

• раздельные и несвязанные каналы управления перемещениями МО по осям X и Y;

• динамика объекта управления вместе с регулятором по каждой координате X, Y описывается инерционным звеном первого порядка с запаздыванием – передаточной функцией

, (9)

где K – коэффициент передачи,

T – постоянная времени,

τ – время запаздывания,

s – оператор Лапласа;

• уставки для каналов управления – требуемые перемещения МО вдоль осей X, Y в физических единицах длины;

• выходные величины каналов управления – фактические перемещения МО вдоль осей X, Y в физических единицах длины.