ФГБОУ ВО

«Уфимский университет науки и технологий»

Кафедра АСУ

Отчет по лабораторной работе №6

по теме «Модель системы оптимального автоматизированного управления на основе SCADA Trace Mode 6 и базы данных Microsoft Access»

по дисциплине «Проектирование и эксплуатация автоматизированных систем управления технологическими процессами»

Выполнил:

Ст. гр. ИВТ-329Б Саляхов А.Ф.

№ЗК 17130458

Проверил:

Доцент каф. АСУ Старцев Ю.В.

Уфа 2024

Теоретическая часть

АСОУ, как следует из названия, представляет собой неразрывную комбинацию автоматизированной системы управления (АСУ) некоторым объектом, и модуля формирования оптимального управления – МФОУ. При этом МФОУ позволяет сформировать оптимальные (в некотором смысле) управляющие воздействия, а АСУ – их отработать в процессе управления объектом. Если производится управление мобильным объектом, то задача МФОУ – планирование оптимальной траектории его перемещения в рабочем пространстве. Решение задачи оптимального управления обычно производится численными методами, носящими общее название «Динамическое программирование».

Метод динамического программирования, предложенный в начале 50-х годов Р. Беллманом, основан на сформулированном им принципе оптимальности. Формулировка принципа оптимальности следующая: конечный участок оптимальной траектории есть также оптимальная траектория.

Динамическое программирование дискретных процессов

Динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. мето В этом случае время вычислений, по сравнению с прямыми методами, можно значительно сократить.

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы.

Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем.

Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.

Словосочетание «динамическое программирование» впервые было использовано Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. 

Слово «программирование» в словосочетании «динамическое программирование» в действительности к традиционному программированию (написанию кода) почти никакого отношения не имеет и имеет смысл как в словосочетании «математическое программирование», которое является синонимом слова «оптимизация». Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи.

Задачи динамического программирования являются многоэтапными, поэтому термин «динамическое программирование» не столько определяет особый тип задач, сколько характеризует методы нахождения решения отдельных классов задач математического программирования.

Общая формулировка задачи динамического программирования. Пусть данная физическая система S находится в некотором начальном состоянии S₀ и является управляемой. Благодаря осуществлению некоторого управления (некоторой операции)   указанная система переходит из начального состояния S₀ в конечное состояние S_КОН . При этом качество каждого из реализуемых управлений  u  характеризуется соответствующим значением функции  W(u).  Задача состоит в том, чтобы из множества возможных управлений  u  найти такое   u*,  при котором функция W(u)  принимает экстремальное значение W(u*).

Рассмотрим основные теоретические аспекты решения задач методом динамического программирования. Будем считать, что состояние рассматриваемой системы S на k-ом шаге ) определяется совокупностью чисел , которые получены в результате реализации управления u_k, обеспечивающего переход системы S из состояния x^(k-1) в состояние x^(k) . 

1. Будем предполагать, что состояние x^(k) , в которое перешла система S , зависит от данного состояния x^(k-1) и выбранного управления u_k и не зависит от того, каким образом система S перешла в состояние x^(k-1).

2. Далее, будем считать, что если в результате реализации k-го шага обеспечен определённый доход, также зависящий от исходного состояния x^(k-1) и выбранного управления u_k ,  равный W(x^(k-1) ; u_k ) , то общий доход за  n шагов составляет

,

где .

Таким образом, сформулированы два условия, которым должна удовлетворять рассматриваемая задача динамического программирования. Первое условие обычно называют условием отсутствия последействий, а второе – условием аддитивности целевой функции задачи оптимизации.

Задача оптимизации в этом случае состоит в отыскании оптимальной стратегии управления, т.е. такой совокупности управлений 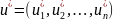, в результате реализации которых система S  за n   шагов переходит из начального состояния x⁽⁰⁾ в конечное x⁽ⁿ⁾ и при этом функция дохода W(u)  принимает наибольшее (экстремальное в общем случае) значение.

Метод динамического программирования основан на применении принципа оптимальности Беллмана: каково бы ни было состояние системы перед очередным шагом, необходимо выбирать управление на этом шаге так, чтобы доход на данном шаге вместе с оптимальным доходом на всех последующих шагах был максимальным.

Важно понимать, что в динамическом программировании речь не идет о простой оптимизации каждого шага управления независимо от других шагов. Шаговое управление должно проводиться дальновидно, с учетом последствий в будущем. Т.е. управление на k-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах, включая данный.

Общая схема перехода системы S из одного состояния в другое в результате управления (принятия решений), воздействий u приведена на рис. 1. Черные кружки обозначают возможные состояния на конкретном шаге.

Рис. 1. Общая схема перехода системы S из начального состояния в конечное

Из принципа оптимальности следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-ом шаге, затем на двух последних шагах, затем на трёх последних шагах и т. д., вплоть до первого шага. Таким образом, решение рассматриваемой задачи динамического программирования целесообразно начинать с определения оптимального решения на последнем, n-ом шаге.

Для того чтобы найти это решение, очевидно, нужно сделать различные предположения о том, как мог окончиться последний шаг, и с учётом этого выбрать управление 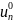, обеспечивающее максимальное значение функции дохода .

Такое управление, выбранное при определённых предположениях о том, как окончился предыдущий шаг, называется  условно оптимальным управлением.

Итак, принцип оптимальности требует находить на каждом шаге условно оптимальное управление для любого из возможных исходов предшествующего шага.

Важно, что среди всех шагов есть один, который можно планировать без учета его последствий. Это - последний шаг, который может быть выбран так, чтобы он принес наибольшую выгоду.

В связи с этим, процесс динамического программирования обычно проводится в направлении от конца к началу, т.е. планируется сначала последний шаг n. При этом делаются различные предположения о том, чем кончился предпоследний (n-1)-й шаг, и для каждого из этих предположений находится условное оптимальное управление на n-м шаге («условное» означает, что управление выбирается исходя из условия, что предпоследний шаг закончился каким-то конкретным образом). После этого процесс продолжается. Проводится оптимизация управления на предпоследнем (n-1)-м шаге с учетом всех возможных предположений об окончании (n-2)-го шага и т.д. вплоть до первого шага.

После определения условно оптимальных управлений на всех шагах определяется оптимальное управление для всего процесса.

 Алгоритм использования метода ДП:

1. Выбираются параметры состояния управляемой системы;

2. Операция расчленяется на этапы;

3. Определяется набор шаговых управлений u_i;

4. Определяется, какой выигрыш приносит на i-м шаге управление  u_i , если перед этим система была в состоянии i-1 (S_i-1 ), т.е. записывается “функция выигрыша”:

W_i = f_i (S_i-1 , u_i); (1)

5. Определяется, как изменяется состояние системы под влиянием управления  u_i на i-м шаге

S_i = φ_i (S_i-1 , u_i) (2)

(переход системы из состояния (i-1) в состояние i ; при этом должны быть определены «функции изменения состояния» (2));

6. Записывается основное рекуррентное соотношение динамического программирования (уравнение Беллмана), выражающее условный оптимальный выигрыш W_i(S_i-1) (начиная с i-го шага и до конца) через уже известную функцию W_i+1(S_i) :

. (3)

Этому выигрышу соответствует условное оптимальное управление на i-м шаге;

7. Производится условная оптимизация последнего (n-го шага) по формуле

(4)

и определяется соответствующее условное оптимальное управление;

8. Производится условная оптимизация (n-1)-го, ( n-2 )-го, и т.д. шагов по формуле (3), полагая в ней i = n-1, n-2, … и т.д. и для каждого из шагов определяется условное оптимальное управление;

9. Производится безусловная оптимизация путем перемещения в прямом направлении – от первого шага к последнему.