
курсовая
.docx
К КУРСОВОЙ РАБОТЕ
ПО ТЕМЕ «РАСЧЕТ ГАЗОВОГО ЦИКЛА И ПОСТРОЕНИЕ ЕГО В PV- И TS-КООРДИНАТАХ»
Вариант № 1
Задание для курсовой работы
Цель работы – расчет газового цикла и построение его в PV- и TS-координатах.
Исходные данные, содержание и последовательность выполнения задания прилагаются на отдельной страницы в приложении к курсовой работе.
Общие сведения
Рассматривая двигатель внутреннего сгорания (ДВС) как классическую термодинамическую систему, т.е. как часть пространства, ограниченную реальными или воображаемыми границами, и исследуя изменения основных параметров ее энергетического состояния, установим, что это за система и какие у нее составные части.
В случае с ДВС очевидно, что изучаемым объектом выступает рабочее тело, воздух или смесь воздуха с парами топлива, что превращается в иную смесь газов в результате процессов горения. Границами для рабочего тела будут стенки цилиндра и поршень.
Чтобы описать состояние рабочего тела и исследовать его основные параметры, используем прямоугольную систему координат.
К основным параметрам состояния относят удельный объем, абсолютное давление, абсолютную температуру. Для удобства построения графиков в декартовых координатах вводится четвертый основной параметр – энтропия, а точнее – ее изменение в термодинамическом процессе.
Реальные процессы ДВС являются весьма сложными и необратимыми, к ним неприменимы методы классической термодинамики. Поэтому применяются следующие допущения, позволяющие идеализировать работу ДВС:
Рабочее тело считается идеальным газом с постоянно теплоемкостью.
Цикл замкнут, количество и качество рабочего тела неизменно.
Теплота к рабочему телу подводится от внешнего изотермического горячего источника и отводится к внешнему изотермическому холодному источнику.
Границы системы могут быть адиабатными.
Разность температур источника теплоты и рабочего тела стремится к нулю.
Отсутствуют сила трения и гидравлические сопротивления.
Основными элементами ДВС являются цилиндр с поршнем, возвратно-поступательные движения которого преобразуются во вращательное движение коленчатого вала с помощью кривошипно-шатунного механизма.
Поршень достигает двух положений, в которых он меняет направление движения. Эти точки называются верхней и нижней мертвыми точками (ВМТ и НМТ).
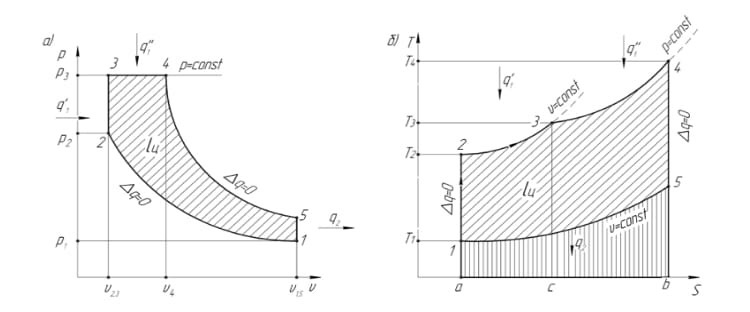
В курсе мы рассматриваем три вида циклов ДВС: цикл Отто с подводом теплоты при постоянном объеме, цикл Дизеля с подводом теплоты при постоянном давлении и цикл Тринклера со смешанными подводом теплоты при постоянных объеме и давлении.
Смешанный цикл представляет собой гибрид циклов Дизиля и Отто, при котором в специальной форкамере, где температура выше температуры самовоспламенения топлива, распыляется топливо, после чего воздух и несгоревшая часть топлива выталкиваются в цилиндр, вследствие чего цилиндр двигается, совершая механическую работу.
В исходных данных степень предварительного расширения равна единице, что в данном случае циклом ДВС будет цикл Отто с подводом теплоты при постоянном объеме (V=const), реализуемые в карбюраторных ДВС.
Схематическое изображение цикла Отто
Определение параметров P, V и Т в характерных точках цикла и определение ρ
В двигателе мы используем в качестве рабочего тела 1 килограмм воздуха, k=1,4
Точка 1:
Из исходных данных известны параметры воздуха P и Т для первой точки цикла.
P = p = 100 КПа
T = 273 K
Согласно уравнению Клапейрона-Менделеева:
V = RT/p =0,287*273/100 = 0,784 м3/кг
Точка 2:
В исходных данных задана степень сжатия ε=V1/V2= 17,7
Из нее можно найти
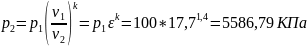
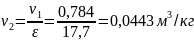
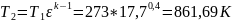
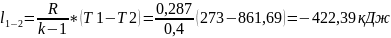

Точка 3:
Степень повышения давления при изохорном подводе тепла λ = p3/p2 =1,99
Ее
можно определить с помощью формулы
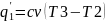
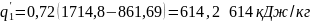
λ =1,99
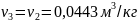
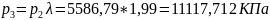
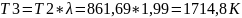
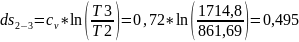
Точка 4:
Степень изобарного расширения
ρ=T3
/ T2 = v3 / v2 =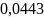 /
=1
/
=1
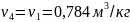
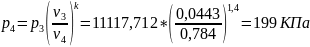
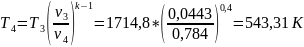
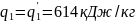
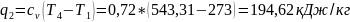
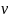 5
=
1=
5
=
1=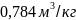
T5
= T4*(
4/
5)k-1=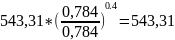

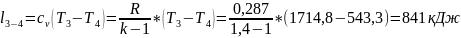
Работа
цикла
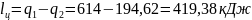
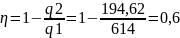 83
83
PV-диаграмма цикла
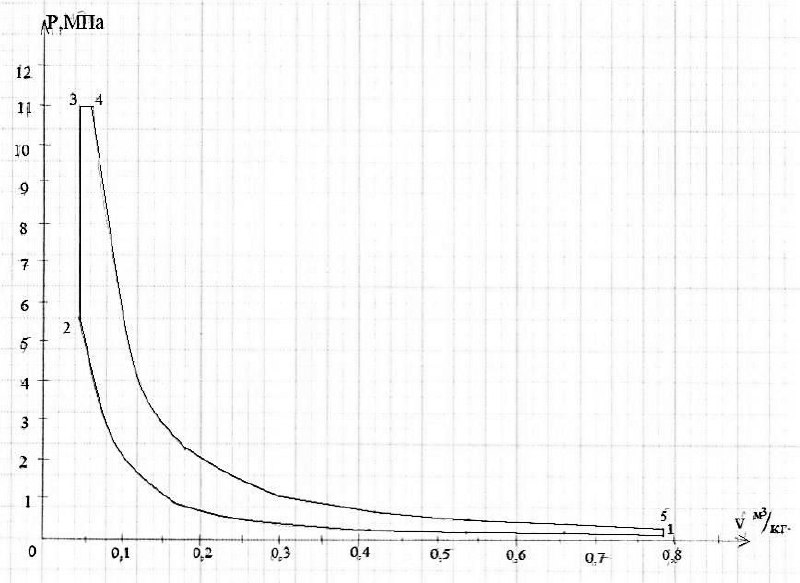
TS-диаграмма цикла
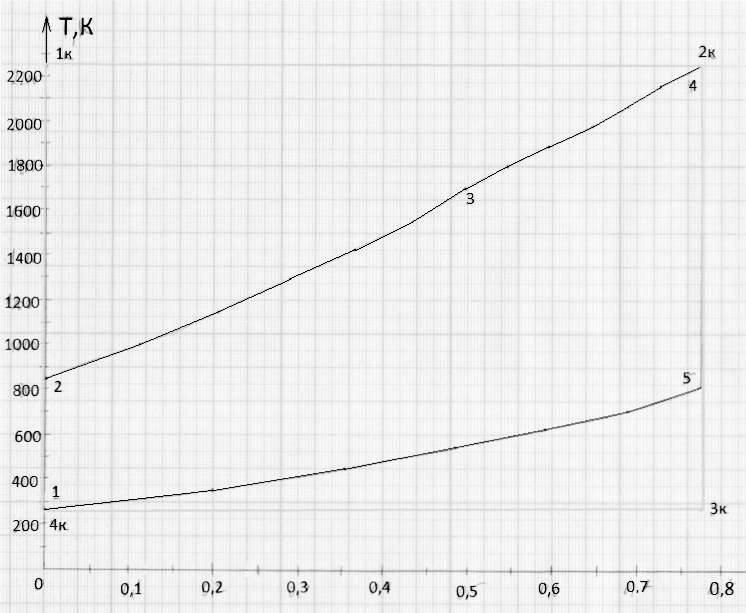
Определение масштабов площадей диаграмм смешанного цикла ДВС
Площадь можно подсчитать несколькими способами: либо вручную с помощью клеток на миллиметровой бумаге, либо с помощью разбиения графика на более простые геометрические фигуры, либо с помощью интеграла.
Для нахождения площади с помощью интеграла подходит формула вычисления площади фигуры, ограниченной графиками непрерывных функций f (x), φ (x) и прямыми х=а, х= b.
Для нахождения q подходит формула для площадь криволинейной трапеции.
Для
PV-диаграммы
работу можно определить как площадь,
ограниченную по бокам изохорами, сверху
и снизу адиабатами, построенными функцией
y
= 6336.164362(0.082236538/x)^1.4
и y=100*(0.85526/x)^1.4, подставив вместо х значения
крайних точек x=0.082236538 и x= 0.85526 (0.082236538 ≤
x
≤0.85526),
получаем определенный интеграл
 dx= 460.378 ~ 460
dx= 460.378 ~ 460
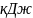 .
.
В условие задачи сказано, что разница между данными, полученными аналитическим и графическим методами, должна быть около 2%. 460/100 =4.60, (462/460)*100%=100.43%, условие выполнено. Совпадает с суммой работ в расчёте.
Уравнения выше описывают и q1 с q2.
q1=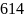 кДж/кг
кДж/кг
q2
=
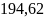 кДж/кг
кДж/кг
У TS-диаграммы верхняя граница состоит из двух функций. С помощью экспоненциальной аппроксимации можно найти обе функции, ограничивающие площадь.
Для
диаграммы верхняя граница y = 860.1*e^1.3889x
и нижняя граница y = 275*e^(1.3889*x), 0 ≤x≤
0.6266, а работа
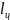
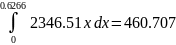
Для
правой верхняя y=1021.8*e^(1x) и нижняя y =
275*e^(1.3889*x), 0.44293366≤
x≤0.739812759,
тогда работа
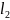
В условие задачи сказано, что разница между данными, полученными аналитическим и графическим методами, должна быть около 2%.
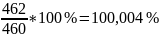 .
Очевидно,
что погрешность соблюдается.
.
Очевидно,
что погрешность соблюдается.
Площадь
под нижней границей диаграммы равняется
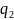 ,
следовательно
,
следовательно
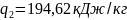
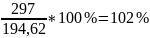
Так
как
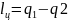 ,
то
,
то
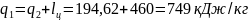 .
.
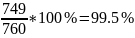
Определение термического КПД цикла двумя способами
Термический КПД с учетом двойного подвода теплоты примет вид:
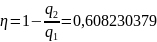
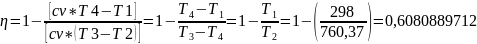
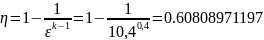
C учетом пропорции Карно:
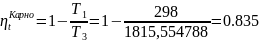
Определение масштабов площадей диаграмм цикла Карно и степени заполнения
Для того, чтобы определить степень заполнения цикла Карно, необходимо его рассчитать аналитически, а также графически.
Достаточно знать максимальную и минимальную температуры в цикле. Так как цикл Карно представляет собой фигуру из двух изотерм и двух адиабат, достаточно просто определить температуру в каждой точке цикла T1=T2, T3=T4. Степень заполнение цикла Карно определяется из Ts-диаграммы, для чего необходимо найти графическое изображение работы на этой диаграмме. Обе изотермы изображаются в виде прямых, параллельных оси S, а адиабаты – это прямые, параллельная оси Т, что вместе нам дает прямоугольник. Площадь для для цикла Карно легко высчитать, рассчитав площадь для фигуры с нижней границей y = 298, верхней границей y = 1815,55, 0≤ x≤ 0.6266
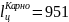
Определяем степень заполнения:
Степень
заполнения
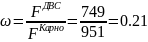
Различные другие процессы могут приближаться к идеальному процессу Карно только с большей или меньшей степенью точности. В данном случае эффективность цикла Отто составляет только 21% от эффективности цикла Карно, учитывая, что в обоих циклы рассчитываются значения для идеального газа. Учитывая, что реальный КПД двигателя, запатентованного Николаусом Аугустом Отто был 15%, достаточно близкое к жизни число.
