
МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра микро- и наноэлектроники
ОТЧЕТ
по лабораторной работе № 8
«Исследование свойств металлических феромагнитных материалов»
Студенты гр. 3291 |
|
Олихнович А. Уханов Е.А. Чупаков В.В. |
Преподаватель |
|
Пермяков Н.В. |
Санкт-Петербург
2024
Цель работы: исследование основных магнитных свойств электротехнической стали, железо-никелевого сплава (пермалоя) или нанокристаллического сплава на основе железа.
Основные понятия и определения
К ферромагнитным относят материалы с
большой положительной магнитной
восприимчивостью
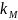 ,
которая сильно зависит от напряженности
магнитного поля H и температуры T.
Ферромагнетикам присуща в интервале
температур от 0 К до температуры Кюри
,
которая сильно зависит от напряженности
магнитного поля H и температуры T.
Ферромагнетикам присуща в интервале
температур от 0 К до температуры Кюри
 спонтанная (самопроизвольная)
намагниченность и их особые свойства
обусловлены доменным строением. Для
осуществления спонтанной намагниченности
необходимо выполнение, по крайней мере,
двух условий:
спонтанная (самопроизвольная)
намагниченность и их особые свойства
обусловлены доменным строением. Для
осуществления спонтанной намагниченности
необходимо выполнение, по крайней мере,
двух условий:
в состав материала должны входить атомы или ионы металлов, имеющих не полностью заполненные внутренние, например 3d, электронные оболочки, создающие нескомпенсированный спиновый момент атома (иона) (к таким металлам относятся железо, никель, кобальт и др.);
структура материала или взаимное расположение атомов должны быть такими, чтобы силы обменного взаимодействия между этими атомами (ионами) приводили к взаимному упорядочению их магнитных моментов.
В ферромагнетиках упорядочение соответствует параллельной ориентации магнитных моментов. При этом можно говорить о спонтанной намагниченности материала, т. е. о суммарном магнитном моменте единицы объема, который определяется видом атомов (ионов) с их специфической величиной магнитного момента и количеством атомов (ионов) в единице объема, определяемом структурой материала.
В отсутствии внешнего магнитного поля состояние, при котором вектор спонтанной намагниченности имел бы во всем образце ферромагнетика одно направление, энергетически не выгодно, так как оно привело бы к большому рассеянию магнитного потока в окружающее пространство, поэтому ферромагнетик самопроизвольно разбивается на отдельные макрообласти (домены), имеющие размеры порядка единиц микрометров.
Внутри каждого домена магнитные моменты атомов имеют одинаковое направление, а моменты отдельных доменов ориентированы друг относительно друга по-разному, так что магнитный поток замкнут внутри ферромагнетика, а суммарный магнитный момент является скомпенсированным и равен нулю.
Соседние домены с различной ориентацией магнитного момента разделены доменными границами, в которых направление спиновых моментов изменяется плавно. Границы (стенки) доменов располагаются и закрепляются, как правило, в местах дефектов, присутствующих в ферромагнетике: (поры, немагнитные включения, границы кристаллитов и т. д.).
П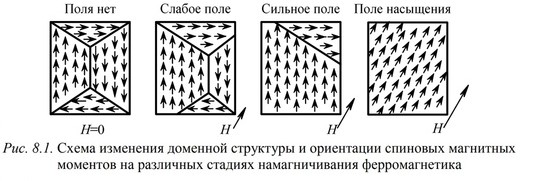 ри
воздействии на ферромагнетик внешнего
магнитного поля происходит перестройка
его доменной структуры, что и приводит
к намагничиванию ферромагнетика
(появлению нескомпенсированного
магнитного момента единицы объема)
(рис. 8.1).
ри
воздействии на ферромагнетик внешнего
магнитного поля происходит перестройка
его доменной структуры, что и приводит
к намагничиванию ферромагнетика
(появлению нескомпенсированного
магнитного момента единицы объема)
(рис. 8.1).
Важнейшим свойством ферромагнетиков является нелинейная зависимость магнитной индукции В от напряженности внешнего магнитного поля Н. Эту зависимость называют начальной кривой намагничивания ферромагнетика, так как она снимается из размагниченного состояния при монотонном увеличении H (рис. 8.2).
На начальном участке кривой намагничивания (I) наблюдается монотонное возрастание магнитной индукции вследствие преобладания процессов обратимого смещения доменных границ. Доменные стенки «упруго прогибаются», как парус. При этом происходит увеличение объема тех доменов, направления магнитных моментов которых образуют наименьший угол с направлением внешнего магнитного поля.
В области более сильных магнитных полей смещение доменных границ приобретает необратимый характер. Доменные стенки под воздействием внешнего поля «срываются с мест закрепления». Здесь кривая намагничивания (II) имеет наибольшую крутизну.
По мере дальнейшего увеличения Н
возрастает роль второго механизма
намагничивания – механизма вращения,
при котором магнитные моменты доменов
постепенно поворачиваются в направлении
поля. На этом участке рост магнитной
индукции замедляется (III). При этом
доменные границы практически исчезают.
Когда все магнитные моменты атомов
ориентируются в доль
поля, наступает магнитное насыщение
(IV).
доль
поля, наступает магнитное насыщение
(IV).
Приняв во внимание, что B = μ H,
по начальной кривой намагничивания
ферромагнетика строится зависимость
статической магнитной проницаемости
μст от напряженности магнитного поля
H. Величину статической магнитной
проницаемости определяют по формуле
H,
по начальной кривой намагничивания
ферромагнетика строится зависимость
статической магнитной проницаемости
μст от напряженности магнитного поля
H. Величину статической магнитной
проницаемости определяют по формуле
μст = B/(μ0H), (8.1)
где μ0 = 4π ∙ 10−7 Гн/м – магнитная постоянная.
Остаточная индукция и коэрцитивная сила являются параметрами статической предельной петли гистерезиса (ПГ), которую получают при медленном циклическом перемагничивании намагниченного до насыщения образца ферромагнетика. Совокупность вершин статических ПГ, соответствующих разным Нm, образуют основную кривую намагни-чивания.
Площадь статической ПГ характеризует потери энергии на гистерезис ЭГ, обусловленные необратимыми процессами смещения доменных границ и вращения векторов намагниченности в единичном цикле перемагничивания. При достаточно быстром изменении Н по величине и знаку (при высокой частоте перемагничивания) зависимость В(Н) описывает динамическую ПГ.
При намагничивании до одинакового предельного значения индукции площадь динамической ПГ металлических ферромагнетиков больше площади статической ПГ на величину, характеризующую потери энергии на вихревые токи ЭВТ.
Мощности потерь на гистерезис Pг и на вихревые токи Pвт в единице массы образца описываются соответственно формулами:
![]()
П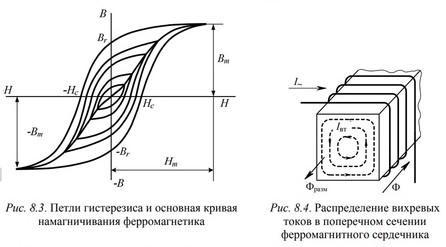 ри
высоких частотах заметный вклад в
мощность потерь вносят потери на вихревые
токи. Вихревые токи возникают в
ферромагнитном материале 60 под действием
ЭДС самоиндукции, пропорциональной
скорости изменения магнитного потока.
Величина вихревых токов зависит от
удельного сопротивления материала. Для
снижения мощности потерь на вихревые
токи Pвт высокочастотные магнитные
материалы должны иметь высокое
сопротивление.
ри
высоких частотах заметный вклад в
мощность потерь вносят потери на вихревые
токи. Вихревые токи возникают в
ферромагнитном материале 60 под действием
ЭДС самоиндукции, пропорциональной
скорости изменения магнитного потока.
Величина вихревых токов зависит от
удельного сопротивления материала. Для
снижения мощности потерь на вихревые
токи Pвт высокочастотные магнитные
материалы должны иметь высокое
сопротивление.
Для металлических ферромагнетиков характерно уменьшение измеряемой величины магнитной проницаемости от частоты, наблюдаемое на достаточно низких частотах, когда инерционность процессов намагничивания еще не проявляется. Это объясняется размагничивающим действием вихревых токов
Плотность потока, создаваемого вихревыми токами, максимальна в центре сердечника и равна нулю на поверхности его. Поэтому результирующая магнитная индукция убывает от поверхности вглубь сердечника.
Относя измеренный поток ко всему сечению сердечника, мы определяем некоторое эффективное значение индукции при данной частоте и соответствующее ему эффективное значение магнитной проницаемости μэф.
Описание установки
И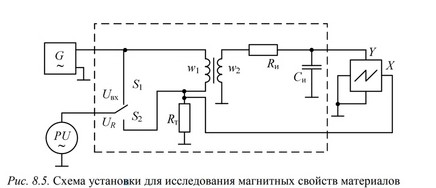 спытания
свойств ферромагнитных материалов
проводятся на установке, схема которой
приведена на рис. 8.5. Установка состоит
из испытательного модуля (выделен
штриховой линией), генератора G
синусоидальных сигналов звуковой
частоты, милливольтметра PU переменного
напряжения и осциллографа N. Испытуемый
материал изготовлен в виде тороидального
сердечника, на который нанесены две
обмотки: первичная с числом витков w1 и
вторичная с числом витков w2.
спытания
свойств ферромагнитных материалов
проводятся на установке, схема которой
приведена на рис. 8.5. Установка состоит
из испытательного модуля (выделен
штриховой линией), генератора G
синусоидальных сигналов звуковой
частоты, милливольтметра PU переменного
напряжения и осциллографа N. Испытуемый
материал изготовлен в виде тороидального
сердечника, на который нанесены две
обмотки: первичная с числом витков w1 и
вторичная с числом витков w2.
На пластины горизонтального отклонения осциллографа (вход канала Х) подается напряжение, снимаемое с резистора Rт (UX = UR). Это напряжение пропорционально току I, протекающему в обмотке w1, следовательно, пропорционально и напряженности магнитного поля Н.
Обработка результатов
Вычислим напряженность поля
 в образце при Rт = 10 Ом;
в образце при Rт = 10 Ом;
 = 0,021 м; w1=100; w2 = 1330;
= 0,021 м; w1=100; w2 = 1330;
 =
=
 Ф;
Ф;
 = 300 кОм; S =
= 300 кОм; S =

 .
.
Пример расчета для первого значения напряженности:
 =
= 15,1578
В/м
15,1578
В/м
Вычислим магнитную индукцию в образце при Rт= 10 Ом;
= 0,021 м; w1=100; w2 = 1330;
=
Ф;
= 300 кОм;
в образце при Rт= 10 Ом;
= 0,021 м; w1=100; w2 = 1330;
=
Ф;
= 300 кОм;
S = .
Пример расчета для первого значения магнитной индукции:
 =
= =
0,1805 Тл
=
0,1805 Тл
Вычислим напряженность поля и магнитную индукцию в образце при Rт= 10 Ом; = 0,021 м; w1=100; w2 = 1330; = Ф; = 300 кОм;
S = .
Найдем статическую магнитную проницаемость по формуле:
 =
= =
9473,68
=
9473,68
Таблица 8.1
Xдел |
|
Yдел |
|
|
|
μ |
4 |
0,200 |
4 |
0,080 |
15,158 |
0,180 |
9473,684 |
3 |
0,150 |
4 |
0,076 |
11,368 |
0,171 |
12000,000 |
3 |
0,125 |
4 |
0,072 |
9,473 |
0,162 |
13642,105 |
2 |
0,100 |
3 |
0,068 |
7,579 |
0,153 |
16105,263 |
2 |
0,075 |
3 |
0,060 |
5,684 |
0,135 |
18947,368 |
1 |
0,050 |
3 |
0,052 |
3,789 |
0,117 |
24631,579 |
1 |
0,025 |
2 |
0,032 |
1,895 |
0,072 |
30315,789 |
0 |
0,013 |
0 |
0,008 |
0,947 |
0,018 |
15157,895 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Построим на одном графике основную
кривую намагничивания и зависимость
статистической магнитной проницаемости
от напряжённости:

Рис 1 - график основной кривой намагничивания и зависимость статистической магнитной проницаемости от напряжённости
Определим площади предельных петель гистерезиса на разных частотах используя САПР КОМПАС3D и занесем их в таблицу 8.2

Таблица 8.2
|
|
Э, мкДж/кг |
|
|
|
|
50 |
1090,475 |
242,100 |
208,803 |
33,297 |
10,440 |
1,665 |
200 |
1976,604 |
438,832 |
230,029 |
41,761 |
46,006 |
|
400 |
2915,502 |
647,280 |
438,477 |
83,521 |
175,391 |
|
600 |
4153,902 |
922,221 |
713,418 |
125,282 |
428,051 |
|
800 |
4719,148 |
1047,713 |
838,910 |
167,042 |
671,128 |
Рассчитаем значения энергии магнитных потерь по приведенным формулам:
Приведем пример расчета для значения частоты = 50 Гц.
 =
= =
3,789395
=
3,789395
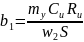 =
=
 =
0,045112782
=
0,045112782
 =
=
 =
242,0998 мкДж/кг
=
242,0998 мкДж/кг
Построим частотную зависимость потерь энергии Э( )
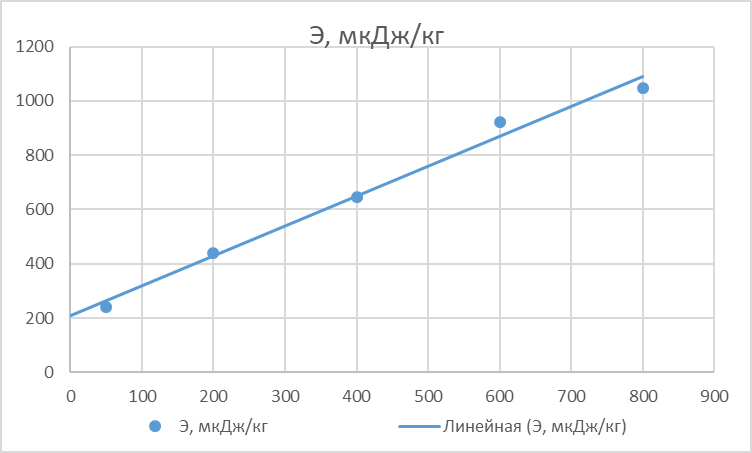
Рис 2 - Частотная зависимость потерь энергии Э( )
Экстраполируем полученную прямую зависимость к =0 и найдем потери на гистерезисе
= 208,8029мкДж/кг
Рассчитаем потери на вихревые токи по формуле

Пример расчета для =50 Гц:
 242,0998-208,8029=33,29692
мкДж/кг
242,0998-208,8029=33,29692
мкДж/кг
Рассчитаем мощности потерь на гистерезисе
 и вихревые токи
и вихревые токи

Пример расчета для =50 Гц:
 =
208,8029*50,0=
10,44015 млВт/кг
=
208,8029*50,0=
10,44015 млВт/кг
 =33,29692*50,0=1,66484598
млВт/кг
=33,29692*50,0=1,66484598
млВт/кг
5) По данным, полученным в 8.3.4, вычислить напряжение на катушке индуктивности с испытуемым сердечником по формуле
Пример расчета для =50 Гц:
 =
= =0,559196
=0,559196
Рассчитаем ее индуктивность для =50 Гц:
 =
= 0,5931
Гн
0,5931
Гн
 =
=
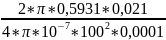 =62299,003
=62299,003
Таблица 8.3
Гц |
|
|
|
L Гн |
|
50 |
0,030 |
0,560 |
0,559 |
0,593 |
62299,003 |
75 |
0,030 |
0,820 |
0,819 |
0,580 |
60862,376 |
100 |
0,030 |
1,040 |
1,040 |
0,552 |
57908,156 |
200 |
0,030 |
1,700 |
1,700 |
0,451 |
47341,112 |
400 |
0,030 |
2,400 |
2,400 |
0,318 |
33419,849 |
600 |
0,030 |
2,800 |
2,800 |
0,248 |
25993,754 |
800 |
0,030 |
3,100 |
3,100 |
0,206 |
21584,328 |
50 |
0,030 |
0,560 |
0,559 |
0,593 |
62299,003 |
По полученным данным построим частотную зависимость эффективной магнитной проницаемости от частоты:

Рис 3 - Частотную зависимость эффективной магнитной проницаемости от частоты μ(f)
Вывод: В итоге выполненной лабораторной работы мы исследовали некоторые свойства железно-никелевого сплава(пермалоя), а именно:
1. Начертили графики зависимости основной кривой намагничивания и зависимость статистической магнитной проницаемости от напряжённости. В зависимости магнитной индукции от напряженности наблюдается монотонное возрастание кривой намагничивания вследствие преобладания процессов обратимого смещения доменных границ. С увеличением напряженности магнитного поля смещение доменных границ приобретает необратимый характер. Здесь кривая намагничивания имеет наибольшую крутизну. По мере увеличения напряженности возрастает роль второго механизма намагничивания – механизма вращения, при котором магнитные моменты доменов постепенно поворачиваются в направлении поля. На этом участке рост магнитной индукции замедляется. Зависимость магнитной проницаемости от напряженности поля. Сначала монотонно возрастает из-за из-за роста доменов, ориентированных вдоль этого поля, а затем снижается из-за того, что роста магнитной индукции нет.
2. Построили график зависимости энергии потерь от частоты. Частотная зависимость потерь энергии линейна так как при низких частотах преобладают потери на гистерезис, а затем, по мере роста частоты, потери на вихревые токи резко возрастают и при высоких частотах становятся преобладающими.
3. Построили частотную зависимость эффективной магнитной проницаемости от частоты. Магнитная проницаемость нелинейно убывает при увеличении частоты из-за размагничивающего действия вихревых токов.

 В
В В
В .
Гц
.
Гц мм^2
мм^2 ,
мкДж/кг
,
мкДж/кг ,
мкДж/кг
,
мкДж/кг ,
млВт/кг
,
млВт/кг ,
млВт/кг
,
млВт/кг В
В В
В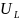 В
В