Результаты исследования ткс постоянных резисторов

№	Тип резистора	Сопротивление, R, _Ом					αR, ppm
		по маркировке	при __˚С (комн.)	при 50˚С	при 80˚С	Диапазон «__˚С – 50˚С»		Диапазон «50˚С – 80˚С»
1	Композитный
2	Углеродный
3	Металло- пленочный
4	Металло- оксидный

3. Графики зависимости сопротивления от температуры для всех исследованных резисторов (рекомендуется построить все четыре графика в одних осях. Для оптимального отображения всех резисторов рекомендуется по оси R(T) использовать логарифмическую шкалу).

4. Подробный расчет сопротивлений резисторов в блоке «треугольник». После получения результата определить вероятное значение каждого резистора при условии, что все резисторы относятся к одному номинальному ряду (например, для результата «1,234 кОм» указать «1,2 кОм из ряда Е24»).

5. Заполненная таблица 1.3 и построенные на одном графике вольт-амперные характеристики маломощного резистора (теоретическая – по формуле Iт(U)=U/Rм и экспериментальная по данным таблицы).

Таблица 1.3

Результаты исследования вах маломощного резистора

U, В	1	2	3	4	…	12	13	…	бах!
Iт, мА
I, мА

6. Выводы с анализом полученных характеристик, описанием соответствия этих характеристик теории, причины отличий.

Лабораторная работа 2. Исследование характеристик пЕременных резисторов

Цель работы – ознакомление с характеристиками нелинейных полупроводниковых резисторов (терморезисторов) и регулировочных резисторов.

Основные сведения о терморезисторах

В работе исследуются температурные характеристики полупроводниковых терморезисторов с отрицательным ТКС (Negative Temperature Coefficient – NTC-термисторы или просто термисторы) и положительным ТКС (Positive Temperature Coefficient – PTC-термисторы или позисторы).

Термисторы состоят из поликристаллической смеси различных спеченных оксидов (например, Fе₂O₃, Zn₂TiO₄, MgCr₂O₄ и TiO₂), сверху компоненты покрываются защитной стеклоэмалью. Они характеризуются круто падающей монотонной зависимостью сопротивления от температуры. Эта зависимость описывается выражением:

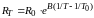, (2.1)

где R_T – сопротивление термистора при текущей температуре T; R₀ – номинальное сопротивление термистора, указываемое для температуры T₀, равной +25 °C или 298 K; B – постоянная, зависящая от материала резистора (значение B обычно лежит в пределах от 1000 до 6000 K). Характер зависимости сопротивления термистора от температуры иллюстрируется рис. 2.1.

По определению температурный коэффициент сопротивления любого резистора находится по формуле (1.1). Если подставить (2.1) в (1.1) и взять производную, то получим следующее выражение для ТКС NTC-термистора:

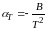. (2.2)

При использовании данной формулы следует помнить, что В и Т выражаются в кельвинах. Из (2.2) следует, что _Т термистора не является константой, а зависит от температуры (это отражено в обозначении _Т вместо _R). Во всей области рабочих температур (обычно от –55 до +155 °С) абсолютное значение _Т термисторов оказывается в десятки раз большим, чем у линейных постоянных резисторов.

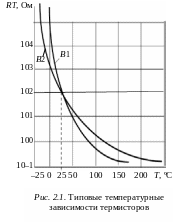
Термисторы широко используются в системах автоматики как датчики температуры и в устройствах компенсации температурного дрейфа выходных сигналов усилителей.

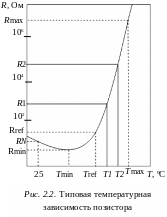
Позисторы обычно изготавливаются на основе поликристаллической керамики из титаната бария (BaTiO₃), легированной различными примесями. Сопротивление позисторов на несколько порядков возрастает после превышения их температуры над некоторым значением (T_ref), что связано с фазовым переходом из сегнетоэлектрического состояния в параэлектрическое (рис. 2.2). Масштаб по оси ординат принято отображать логарифмическим, поскольку рост сопротивления от температуры носит почти экспоненциальный характер.

В области резкого увеличения сопротивления _Т позистора приблизительно постоянен. Тогда, если на этом участке известны два значения сопротивления, например, R₁ и R₂, которые соответствуют двум температурам Т₁ и Т₂, то для _Т будет справедливо:

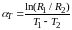. (2.3)

В пределах этого температурного диапазона, зная сопротивление для некоторой температуры, можно рассчитать, каким станет сопротивление при другой температуре:

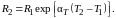(2.4)

С помощью формулы (2.4) может быть рассчитано сопротивление позистора для выбранной температуры на основании его справочных данных. В этом случае вместо сопротивления R₁ и температуры T₁ используют R_ref и T_ref соответственно. Позисторы нашли широкое применение в схемах ограничения тока, а также как высокочувствительные датчики температуры.

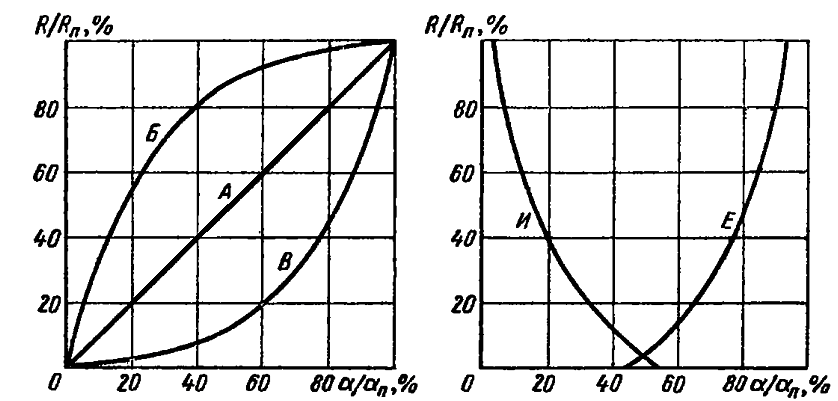
Рис. 2.3. Типы функциональных зависимостей переменных регулировочных резисторов

Для механического переменного резистора (регулировочного резистора) исследуется его функциональна зависимость – значение сопротивления от угла поворота, которое может изменяться по различным законам (рис 2.3).

По характеру функциональной зависимости переменные резисторы делятся на линейные – типа А и нелинейные – типов Б, В, И, Е и др. Характер нелинейной зависимости определяется схемными задачами, для решения которых предназначен резистор. Наиболее распространенные зависимости логарифмические (Б) и обратнологарифмические (В). Резисторы с такими зависимостями применяются для регулировок громкости и тембра звука, яркости свечения индикаторов и т.п. Встречаются резисторы с характеристиками типа И или Е, а также с синусными, косинусными зависимостями, используемые в устройствах автоматики и вычислительной техники.

Порядок выполнения исследований

1. Включить стенд и мультиметры, установить мультиметр DT890B+ в необходимый диапазон измерения сопротивления (в зависимости от номинала термистора), а мультиметр M890C+ – в диапазон измерений температуры, записать его показания в протокол.

2. Поместить термистор B57045 (R₀ = 10 кОм или 1 кОм) в нагревательный элемент, собрать схему в соответствии с рис. 1.2. Включить нагревательный элемент. Снять зависимость сопротивления термистора от комнатной температуры до температуры 80 °С. Результаты исследований занести в протокол.

3. Повторить измерения для термистора B57164 (R₀ = 2 кОм).

4. Заменить термистор на позистор и повторить измерения по п. 3, нагревая его до температуры 90 ^оС (изменять диапазон мультиметра в зависимости от роста сопротивления). Результаты занести в протокол.

5. Для измерения вольтамперной характеристики позистора в режиме саморазогрева собрать схему в соответствии с рис. 2.3.

6. Постепенно увеличивая напряжение источника питания от 0 до 20 В, снять зависимость тока, протекающего через позистор, от подаваемого на него напряжения. Результаты исследований занести в протокол.

7. Для исследования переменного резистора собрать схему в соответствии с рис 2.5.: подключить 1 и 2 выводы резистора к мультиметру и поместить ручку исследуемого резистора в крайнее левое положение, соответствующее 0° поворота.

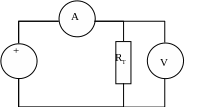
Рис. 2.4. Схема измерения ВАХ позистора

Рис. 2.5. Схема измерения функциональной зависимости потенциометра

9. Изменяя положение ручки потенциометра, снять зависимость сопротивления резистора от угла поворота ручки. Измерения при этом необходимо производить через каждые 30 градусов поворота. Показания мультиметра записать в протокол.

10. Снова поместить ручку исследуемого резистора в крайнее левое положение и подключить 2 и 3 выводы потенциометра к мультиметру.

11. Повторить измерения сопротивления резистора от угла поворота ручки, записать полученные значения протокол.

14. Подключить дополнительный резистор параллельно с потенциометром (рис 2.6).

Рис. 2.6. Схема измерения функциональной зависимости потенциометра с параллельным резистором

15. Повторить измерения пп. 7-11 для потенциометра зависимости сопротивления от угла поворота ручки и занести данные в нижнюю строку табл. 2.4

Содержание отчета

1. Цель работы, схемы измерений (рис. 1.3, а и рис. 2.4).

2. Заполненная для каждого термистора таблица 2.1, в которую должны быть внесены результаты расчета _Т. Значения _Т рассчитываются по данным соседних столбцов таблицы с помощью формулы (1.1). Т и R_T каждого столбца (кроме первого и последнего) участвуют в расчетах дважды как левая и правая границы выделяемых интервалов.

Таблица 2.1