Центральная предельная теорема

переписать в тетрадь с лекциями, выделяя ключевые слова подчеркиванием

Закон больших чисел и предельные теоремы

Закон больших чисел базируется на общем принципе, согласно которому

Совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Неравенство Маркова

Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство

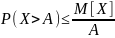или для противоположного события .

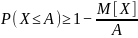Неравенство Маркова применимо и к дискретным, и к непрерывным случайным величинам.

Задача:

Среднее число вызовов, поступающих на станцию скорой помощи в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов

а) превысит 400;

б) будет не более 500.

Решение:

а) По условию М[X]=300. Тогда с использованием неравенства Маркова в форме оценим требуемую вероятность

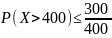
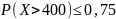
б) Оценим требуемую вероятность с использованием неравенства Маркова в форме .

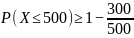
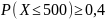
Неравенство Чебышева

Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева

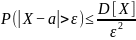или для противоположного события ,

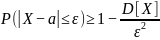где а=M[X], ɛ>0.

Неравенство Чебышева применимо и к дискретным, и к непрерывным случайным величинам.

Частные случаи:

а) Для случайной величины Х=m, имеющей биноминальный закон распределения с матожиданием M[X]=np и дисперсией D[X]=npq :

.

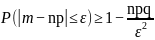б) Для частости (относительной частоты) 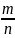события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р=M[ ] и имеющей дисперсию D[ ]= :

.

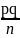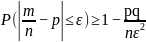Задача:

Средний расход воды на производстве составляет 1000 л в день, а среднее квадратическое отклонение σ этой величины не превышает 200 л.

Оценить вероятность того, что расход воды на производстве в любой выбранный день не превысит 2000 л.

Решение:

Пусть случайная величина Х-расход воды на производстве за день.

Ее математическое ожидание M[X]=1000 л, а дисперсию можно записать через среднее квадратическое отклонение D[X]=σ² , тогда из исходных данных D[X] 200².

Нужно оценить P( ).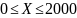

Так как границы интервала симметричны относительно матожидания M[X]=1000, его можно записать как 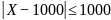и воспользоваться неравенством Чебышева .

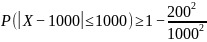
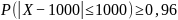
Закон больших чисел (теорема Чебышева)

Если дисперсии n независимых случайных величин Х₁, Х₂, …,Х_n ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин Х₁, Х₂, …,Х_n сходится по вероятности к средней арифметической величине их матожиданий M[X₁]=a₁, M[X₂]=a₂, …, M[X_n]=a_n, то есть

.

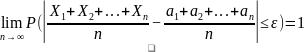Смысл закона больших чисел (теоремы Чебышева) заключается в следующем:

При большом числе n случайных величин Х₁, Х₂, …,Х_n практически достоверно, что их среднее арифметическое 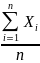- величина случайная, как угодно мало отличается от неслучайной величины 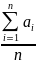, то есть практически перестает быть случайной.

Теорема Бернулли

Частость (относительная частота) события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности p этого события в отдельном испытании

.

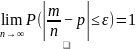Теорема Бернулли дает теоретическое обоснование замены неизвестной вероятности события его частостью или статистической вероятностью, полученной в n повторных независимых испытаниях, проводимых при одном и том же комплексе условий.

Теорема Пуассона

Частость события в n повторных независимых испытаниях, в каждом из которых оно может произойти с вероятностями p₁, p₂, …, p_n при неограниченном увеличении числа n сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях, то есть

.

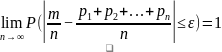Если сравнить теоремы Пуассона и Бернулли то увидим, что теорема Бернулли является частным случаем теоремы Пуассона при p₁=p₂=…=p_n=p, а теорема Пуассона более общая, так как вероятности события в испытаниях p₁, p₂, …, p_n в ней различны.

Центральная предельная теорема (теорема Ляпунова)

Если Х₁, Х₂, …,Х_n – независимые случайные величины, у каждой из которых существует матожидание M[X_i]=a_i и дисперсия D[X_i]=σ_i², то закон распределения суммы 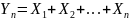при n→ неограниченно приближаются к нормальному с матожиданием 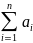и дисперсией .

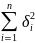Важно чтобы в сумме не было слагаемых, влияние которых на Y_n было бы подавляюще велико по сравнению с влиянием всех остальных, а также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных.

Нормальный закон распределения является предельным законом, к которому при определенных условиях стремится сумма случайных величин с любыми законами распределения.

4

© Е.В. Сидорова, к.т.н., доцент НГТУ им. Р.Е. Алексеева