Основные законы распределения

переписать в тетрадь с лекциями, выделяя ключевые слова подчеркиванием

Основные законы распределения СЛУЧАЙНЫХ ВЕЛИЧИН

Биноминальный закон распределения

Дискретная случайная величина Х имеет биноминальный закон распределения, если она принимает значения 0, 1, 2, …, n с вероятностями , где q=1-p.

Ряд распределения биноминального закона:

xi	0	1	2	…	n
pi	qn	npqn-1		…	pn

Математическое ожидание случайной величины Х, распределенной по биноминальному закону М[X]=np, дисперсия D[X]=npq.

Закон распределения Пуассона

Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m, … с вероятностями .

Ряд распределения имеет вид:

xi	0	1	2	…	m	…
pi	e-	e-		…		…

Математическое ожидание случайной величины Х, распределенной по закону Пуассона М[X]=, дисперсия D[X]=.

При р→0, n→, np→=const закон распределения Пуассона является предельным случаем биноминального закона. Так как при этом вероятность р распределения события А очень мала, то закон распределения Пуассона называют законом редких явлений.

Геометрическое распределение

Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения 1, 2,…, m, … с вероятностями

, где q=1-p

Ряд геометрического распределения

xi	1	2	3	…	m	…
pi	p	pq	pq2	…	pqm-1	…

M[X]= ; D[X]= .

Задача

Проводится проверка большой партии деталей до обнаружения бракованной. Составить закон распределения числа проверенных деталей. Найти его мат ожидание и дисперсию, если известно, что вероятность брака для каждой детали равна 0,1.

Решение:

Пусть случайная величина Х-число бракованных деталей до обнаружении бракованной. Вероятность обнаружения брака р=0,1, q=1-0,1=0,9.

Так как множество возможных значений Х гипотетически бесконечно, но счетно, то это величина относится к дискретному типу. Следовательно закон ее распределения можно представить рядом распределения:

xi	1	2	3	…	m	…
pi	p	pq	pq2	…	pqm-1	…

xi	1	2	3	…	m	…
pi	0,1	0,09	0,081	…	0,1*0,9m-1	…

M[X]= = =10,

D[X]= = =90

Равномерный закон распределения

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его, то есть

Тогда ее функция распределения имеет вид:

M[X]= ,

D[X]= .

Случайная величина Х распределенная равномерно на отрезке [0;1] служит для получения случайных величин с любым законом распределения.

Задача

Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени.

Какова вероятность того, что ждать пассажиру придется не более полминуты.

Найти мат ожидание и средне квадратичное отклонение X- времени ожидания поезда.

Решение:

Пусть случайная величина Х- время ожидания поезда на временном отрезке [0;2]. Это непрерывная случайная величина, так как ее возможные значения представлены диапазоном. Кроме того она подчинена равномерному закону распределения.

Ее плотность .

Найдем вероятность того, что пассажиру придется ждать не более полминуты, используя свойство плотности вероятности непрерывной случайной величины:

Рассчитаем мат ожидание M[X]= мин,

найдем дисперсию D[X]= ,

а затем средне квадратичное отклонение .

Экспоненциальный (показательный) закон распределения

Непрерывная случайная величина Х имеет экспоненциальный (показательный) закон распределения с параметром , если ее плотность вероятности имеет вид:

Функция распределения случайной величины Х, распределенной по экспоненциальному закону, есть

Математическое ожидание M[X]= ,

а дисперсия D[X]= .

Экспоненциальный закон распределения имеет большое значение при решении задач по теории надежности и систем массового обслуживания.

Экспоненциальный закон и только он обладает важным свойством:

Если промежуток времени Т, распределенный по экспоненциальному (показательному) закону, уже длился некоторое время t, то это никак не влияет на закон распределения оставшейся части T-t промежутка, то есть закон распределения оставшейся части остается таким же, как и всего промежутка Т.

Нормальный закон распределения (Гаусса)

Нормальный закон распределения один из самых часто используемых на практике. Главная особенность состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при некоторых условиях.

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами a и σ², если ее плотность вероятности имеет вид:

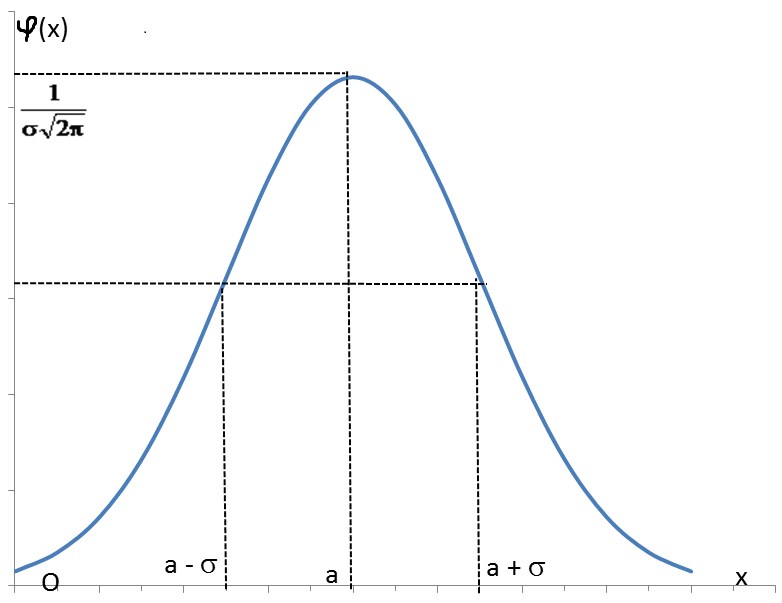
График φ(х) плотности вероятности нормального закона распределения симметричен относительно прямой х=а, имеет максимум в точке х=а равный и две точки перегиба х=а±σ.

Функция распределения нормально распределенной случайной величины

Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. M[X]=a, а ее дисперсия - параметру σ², то есть D[X]= σ².

Выясним, как будет меняться нормальная кривая плотности вероятности при изменении параметров а и σ².

Если σ=const и меняется параметр а (а₃<a₂<a₁), то нормальная кривая плотности будет смещаться вдоль оси абсцисс, не меняя форму (анализируем формулу максимума , точек перегиба х=а±σ и ось симметрии х=а).

Если а=const и меняется параметр σ (σ₁<σ₂<σ₃), то меняется ордината максимума кривой плотности .

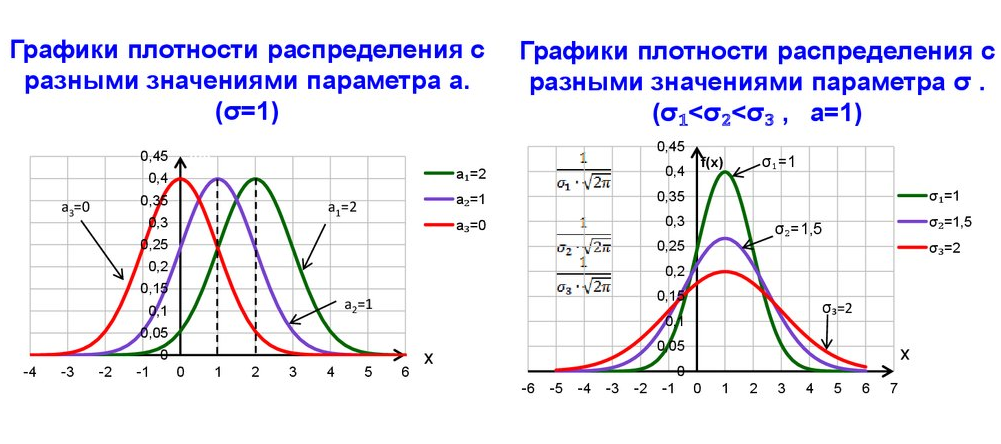
Таким образом, параметр а (математическое ожидание) характеризует положение, а параметр σ² (дисперсия) – форму кривой плотности нормального распределения.

!!!!! Нормальный закон распределения случайной величины с параметрами а=0, σ²=1, то есть N(0;1) называется стандартным нормальным законом.

Для стандартного нормального закона (а=0, σ²=1), функции плотности вероятности φ₀(х) и распределения F(x) примут вид:

;

.

Самостоятельно построить график плотности стандартного нормального закона.

Рассмотрим свойства случайной величины, распределенной по нормальному закону:

1. Вероятность попадания случайной величины Х, распределенной по нормальному закону с параметрами а и σ, в интервал [x₁;x₂] равна

, где ,

2. Правило « трех сигм»

Если случайная величина Х имеет нормальный закон распределения с параметрами а и σ , то есть Х N(а; σ²), то практически достоверно, что ее значения заключены в интервале (а-3σ; а+3σ).

7

© Е.В. Сидорова, к.т.н., доцент НГТУ им. Р.Е. Алексеева