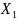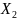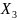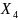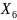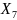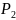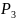23-ИСТ-1-1_Какушкина_Ольга_Лаб3_ТИ

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

Н ИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. Р.Е.АЛЕКСЕЕВА

Институт радиоэлектроники и информационных технологий

Кафедра «Электроника и сети ЭВМ»

ОТЧЁТ

по Лабораторной работе №3

по дисциплине

Теория информаций, данные, знания.

РУКОВОДИТЕЛЬ:

Баранов Д.В.

____________________

(подпись) (фамилия, и.,о.)

Какушкина О.В.

СТУДЕНТ:

_________________

(подпись) (фамилия, и.,о.)

23-ИСТ-1-1

(шифр группы)

Работа защищена «___» ____________

С оценкой ________________________

Нижний Новгород

2025

Цель работы

Научиться строить линейные корректирующие коды на основе порождающих матриц для обнаружения и исправления ошибок в кодовых словах. Исследовать алгоритмы кодирования и декодирования сообщений с помощью линейных кодов и изучить способы их технической реализации.

Ход работы

Пусть требуется построить порождающую матрицу для линейного блокового кода, способного исправлять одиночную ошибку при передаче информационных векторов из 8 символов (10111010, 10110001, 00010001).

Получим порождающую матрицу в приведенной форме:

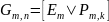
Поскольку число исправляемых ошибок t = 1, то кодовое расстояние d для линейного корректирующего кода будет:

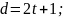
Отсюда получим

Так как длина информационных векторов m = 8, то число строк порождающей матрицы линейного блокового кода должно быть равно 8. Число столбцов порождающей матрицы равно длине кодовых векторов где k - число проверочных символов, которое при d = 3 может быть найдено по формуле:

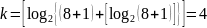
Отсюда получим

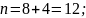
Таким образом, искомый линейный блоковый код является (12,8,3) – кодом.

Поскольку вес каждой строки матрицы-дополнения Р должен быть , то в качестве строк матрицы Р примем четырехзначные двоичные комбинации с числом единиц 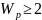. Комбинации выберем так, чтобы число единиц в столбцах матрицы Р было одинаковым. Заданным требованиям удовлетворяет следующий набор: 1111, 1101 , 1100, 1001, 1010, 0111, 0011, 0110.

Окончательный вид порождающей матрицы будет:

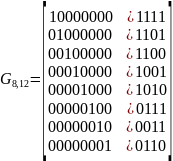
Получим для заданных информационных векторов 10111010, 10110001, 00010001 кодовые вектора линейного (12, 8, 3) - кода. Для этого найдем значения проверочных символов для каждого информационного вектора путем суммирования по модулю 2 тех строк матрицы Р, номера которых совпадают с номерами разрядов, содержащих единицы в информационных векторах:

1. 10111010:

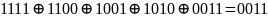
2. 10110001:

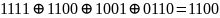
3. 00010001:

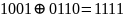
Отсюда искомые кодовые векторы будут:

; ;

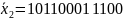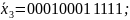
Запишем систему проверок для найденной матрицы P:

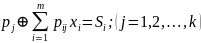
Система проверок будет иметь следующий вид:

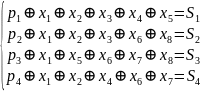
Для того, чтобы знать, какая комбинация синдрома S будет соответствовать ошибке в определенном разряде принятого кодового вектора, построим проверочную матрицу линейного блокового кода:

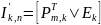
Транспонированная матрица-дополнение P будет выглядеть следующим образом:

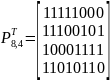
Отсюда проверочная матрица линейного блокового кода будет:

1	1	1	1	1	0	0	0	1	0	0	0
1	1	1	0	0	1	0	1	0	1	0	0
1	0	0	0	1	1	1	1	0	0	1	0
1	1	0	1	0	1	1	0	0	0	0	1

Предположим, что в переданных кодовых векторах произошли следующие ошибки (выделены жирным шрифтом):

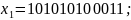
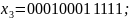
Найдем согласно полученной системе проверок для каждого переданного кодового вектора синдром :

1) Для кодового вектора :

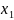x1	x2	x3	x4	x5	x6	x7	x8	p1	p2	p3	p4
1	0	1	0	1	0	1	0	0	0	1	1

Синдром 1001 показывает, что значение символа следует заменить на противоположное.

2) Для кодового вектора :

x1	x2	x3	x4	x5	x6	x7	x8	p1	p2	p3	p4
1	0	1	1	0	0	1	1	1	1	0	0

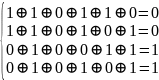
Синдром 0011 показывает, что значение символа следует заменить на противоположное.

3) Для кодового вектора :

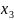x1	x2	x3	x4	x5	x6	x7	x8	p1	p2	p3	p4
0	0	0	1	0	0	0	0	1	1	1	1

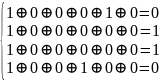
Синдром 0110 показывает, что значение символа следует заменить на противоположное.

Вывод:

В ходе выполнения лабораторной работы я научилась строить линейные корректирующие коды на основе порождающих матриц для обнаружения и исправления ошибок в кодовых словах.