МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
Н ИЖЕГОРОДСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
ИЖЕГОРОДСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ им. Р.Е.АЛЕКСЕЕВА
Институт радиоэлектроники и информационных технологий
Кафедра «Информатика и системы управления»
ОТЧЁТ
по Лабораторной работе №1
по дисциплине
Теория информаций, данные, знания.
РУКОВОДИТЕЛЬ:
Баранов
Д. Б.
____________________
(подпись) (фамилия, и.,о.)
Какушкина
О. В.
_________________
(подпись) (фамилия, и.,о.)
23-ИСТ-1-1
(шифр группы)
Работа защищена «___» ____________
С оценкой ________________________
Нижний Новгород
2025
Цель работы
Изучение методов эффективного кодирования дискретных сообщений в отсутствии помех и освоение способов практической реализации этих методов на ЭВМ.
Задания и порядок выполнения работы
Эффективному кодированию подлежит массив, представляющий собой последовательность из 1 и 0, при этом вероятность 1 равна p.
При заданном значении p (0.2-0.4) реализовать кодирование блоками по методу Шеннона-Фано и методу Хаффмана. Длина блока выбирается равной n= 2,3,4.
Оценить эффективность кодирования массива и сравнить её с теоретическими предельными возможностями.
Исследовать зависимость эффективности кодирования от длины блока и значения энтропии источника.
Описание алгоритмов кодирования
Алгоритм кодирования методом Шеннона-Фано:
Пусть имеется множество сообщений
Все сообщения располагаются в порядке убывания их вероятностей.
Упорядоченное множество сообщений делится на две части: верхнюю часть и нижнюю часть, причем так, чтобы разность между суммой вероятностей в верхней и нижней части была минимальной.
После этого сообщениям в верхней части ставится в соответствие 1, а в нижней – 0.
Далее аналогичные действия производятся с каждой из частей. Вновь полученные подмножества сообщений снова аналогичным образом делятся на две части и т.д., до получения по одному сообщению в каждом из подмножеств.
В результате каждому сообщению будет соответствовать своя последовательность из нулей и единиц, т.е. кодовое слово
Алгоритм кодирования методом Хаффмана:
Все сообщения располагаются в порядке убывания их вероятностей.
Два самых маловероятных сообщения объединяются в одно событие, вероятность которого равна сумме вероятностей, объединяемых событий, причем верхнему событию ставится в соответствие 1, а нижнему 0.
Получился новый массив сообщений с количеством состояний на единицу меньшим по сравнению с предыдущим массивом, если два последних события считать одним более крупным событием. Далее преобразуем этот массив в соответствии с пунктом 2. Полученный массив вновь подвергаем указанным преобразованиям и так до тех пор, пока не будет исчерпан весь массив.
Геометрически результат можно представить в виде дерева, где кодовое слово выражается последовательностью ветвей с соответствующем сообщением.
Ход работы
Для эффективного кодирования с помощью 1 и 0 нужно выбрать вероятность появления
1 или 0 от 0,2 до 0,4.
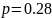 .
Тогда
.
Тогда
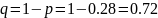
Кодирование по Шеннону (p=0.28; q=0.72; n=2)
а) обозначение за 0: q, а за 1: p
N |
|
|
|
1 |
0 |
0 |
P=q2=0,5184 |
2 |
0 |
1 |
P=pq=0,2016 |
3 |
1 |
0 |
P=pq=0,2016 |
4 |
1 |
1 |
P=p2=0,0784 |
б) Располагаем в порядке убывания вероятностей и получаем кодовые слова:
N |
|
Кодовые слова |
l |
|
||
0 |
0,5184 |
1 |
|
|
1 |
0,5184 |
1 |
0,2016 |
0 |
1 |
|
2 |
0,4032 |
2 |
0,2016 |
0 |
0 |
1 |
3 |
0,6048 |
3 |
0,0784 |
0 |
0 |
0 |
3 |
0,2352 |
Средняя длина кодового слова:
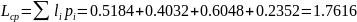
Кодирование по Шеннону (p=0.28, q=0.72, n=3)
а) обозначение за 0: q, а за 1: p
N |
|
|
||
1 |
0 |
0 |
0 |
P=q3=0,3732 |
2 |
0 |
0 |
1 |
P=q2p=0,1451 |
3 |
0 |
1 |
0 |
P=q2p=0,1451 |
4 |
0 |
1 |
1 |
P=qp2=0,0564 |
5 |
1 |
0 |
0 |
P=q2p=0,1451 |
6 |
1 |
0 |
1 |
P=qp2=0,0564 |
7 |
1 |
1 |
0 |
P=qp2=0,0564 |
8 |
1 |
1 |
1 |
P=p3=0,0219 |
б) Располагаем в порядке убывания и получаем кодовые слова:
N |
|
|
l |
|
|||
1 |
0,3732 |
1 |
1 |
|
|
2 |
0,7464 |
2 |
0,1451 |
1 |
0 |
|
|
2 |
0,2902 |
3 |
0,1451 |
0 |
1 |
1 |
|
3 |
0,4353 |
4 |
0,1451 |
0 |
1 |
0 |
|
3 |
0,4353 |
5 |
0,0564 |
0 |
0 |
1 |
1 |
4 |
0,2256 |
6 |
0,0564 |
0 |
0 |
1 |
0 |
4 |
0,2256 |
7 |
0,0564 |
0 |
0 |
0 |
1 |
4 |
0,2256 |
8 |
0,0219 |
0 |
0 |
0 |
0 |
4 |
0,0876 |
Средняя длина кодового слова:
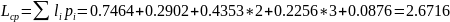
Кодирование по Шеннону (p=0.28, q=0.72, n=4)
а) обозначение за 0: q, а за 1: p
N |
|
|
|||
1 |
0 |
0 |
0 |
0 |
P=q4=0.2687 |
2 |
0 |
0 |
0 |
1 |
P=q3p=0.1045 |
3 |
0 |
0 |
1 |
0 |
P=q3p=0.1045 |
4 |
0 |
0 |
1 |
1 |
P=q2p2=0.0406 |
5 |
0 |
1 |
0 |
0 |
P=q3p=0.1045 |
6 |
0 |
1 |
0 |
1 |
P=q2p2=0.0406 |
7 |
0 |
1 |
1 |
0 |
P=q2p2=0.0406 |
8 |
0 |
1 |
1 |
1 |
P=qp3=0.0158 |
9 |
1 |
0 |
0 |
0 |
P=q3p=0.1045 |
10 |
1 |
0 |
0 |
1 |
P=q2p2=0.0406 |
11 |
1 |
0 |
1 |
0 |
P=q2p2=0.0406 |
12 |
1 |
0 |
1 |
1 |
P=qp3=0.0158 |
13 |
1 |
1 |
0 |
0 |
P=q2p2=0.0406 |
14 |
1 |
1 |
0 |
1 |
P=qp3=0.0158 |
15 |
1 |
1 |
1 |
0 |
P=qp3=0.0158 |
16 |
1 |
1 |
1 |
1 |
P=p4=0.0061 |
б) Располагаем в порядке убывания вероятностей и получаем кодовые слова:
N |
|
|
|
|
|
|
|
|
l |
|
1 |
0.2687 |
1 |
1 |
|
|
|
|
|
2 |
0,5374 |
2 |
0.1045 |
1 |
0 |
1 |
|
|
|
|
3 |
0,3135 |
3 |
0.1045 |
1 |
0 |
0 |
|
|
|
|
3 |
0,3135 |
5 |
0.1045 |
0 |
1 |
1 |
|
|
|
|
3 |
0,3135 |
9 |
0.1045 |
0 |
1 |
0 |
1 |
|
|
|
4 |
0,418 |
4 |
0.0406 |
0 |
1 |
0 |
0 |
|
|
|
4 |
0,1624 |
6 |
0.0406 |
0 |
0 |
1 |
1 |
|
|
|
4 |
0,1624 |
7 |
0.0406 |
0 |
0 |
1 |
0 |
1 |
|
|
5 |
0,203 |
10 |
0.0406 |
0 |
0 |
1 |
0 |
0 |
|
|
5 |
0,203 |
11 |
0.0406 |
0 |
0 |
0 |
1 |
1 |
|
|
5 |
0,203 |
13 |
0.0406 |
0 |
0 |
0 |
1 |
0 |
|
|
5 |
0,203 |
8 |
0.0158 |
0 |
0 |
0 |
0 |
1 |
1 |
|
6 |
0,0948 |
12 |
0.0158 |
0 |
0 |
0 |
0 |
1 |
0 |
|
6 |
0,0948 |
14 |
0.0158 |
0 |
0 |
0 |
0 |
0 |
1 |
|
6 |
0,0948 |
15 |
0.0158 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
7 |
0,1106 |
16 |
0.0061 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0,0427 |
Средняя длина кодового слова:
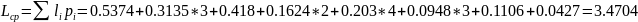
Кодирование по Хаффману (p=0.28; q=0.72; n=2)
а) обозначение за 0: q, а за 1: p
N |
|
|
|
1 |
0 |
0 |
P=q2=0,5184 |
2 |
0 |
1 |
P=pq=0,2016 |
3 |
1 |
0 |
P=pq=0,2016 |
4 |
1 |
1 |
P=p2=0,0784 |
б) Располагаем в порядке убывания вероятностей и получаем кодовые слова:
1
1
1

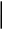

1


0

0
0
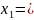 0
0
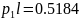
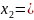 01
01
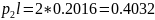
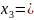 001
001
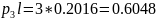
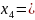 000
000
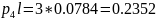
Средняя длина кодового слова:
Кодирование по Хаффману (Р=0.28; q=0.72; n=3)
а) обозначение за 0: q, а за 1: p
N |
|
|
|||
1 |
0 |
0 |
0 |
P=q3=0,3732 |
|
2 |
0 |
0 |
1 |
P=q2p=0,1451 |
|
3 |
0 |
1 |
0 |
P=q2p=0,1451 |
|
4 |
0 |
1 |
1 |
P=qp2=0,0564 |
|
5 |
1 |
0 |
0 |
P=q2p=0,1451 |
|
6 |
1 |
0 |
1 |
P=qp2=0,0564 |
|
7 |
1 |
1 |
0 |
P=qp2=0,0564 |
|
8 |
1 |
1 |
1 |
P=p3=0,0219 |
|
б) Располагаем в порядке убывания вероятностей и получаем кодовые слова:

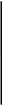
1
0,3752
1

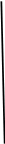
0,1451

2,0016
1


1
0,1451
0,2902


1,6264
1,3362
0
0,1451

0
1

0
1
0,0564

0,1128
0
0,0564

1,1911
0
1
0,0564

0,0783
0
0
0,0219
1
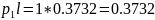
001
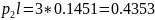
011
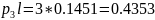
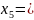 010
010
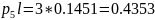
00011
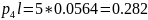
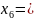 00010
00010
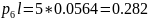
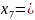 00001
00001
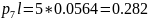
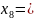 00000
00000
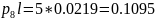
Средняя длина кодового слова:
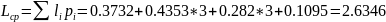
Кодирование по Хаффману (Р=0.28; q=0.72; n=4)
а) обозначение за 0: q, а за 1: p
N |
|
|
|||
1 |
0 |
0 |
0 |
0 |
P=q4=0.2687 |
2 |
0 |
0 |
0 |
1 |
P=q3p=0.1045 |
3 |
0 |
0 |
1 |
0 |
P=q3p=0.1045 |
4 |
0 |
0 |
1 |
1 |
P=q2p2=0.0406 |
5 |
0 |
1 |
0 |
0 |
P=q3p=0.1045 |
6 |
0 |
1 |
0 |
1 |
P=q2p2=0.0406 |
7 |
0 |
1 |
1 |
0 |
P=q2p2=0.0406 |
8 |
0 |
1 |
1 |
1 |
P=qp3=0.0158 |
9 |
1 |
0 |
0 |
0 |
P=q3p=0.1045 |
10 |
1 |
0 |
0 |
1 |
P=q2p2=0.0406 |
11 |
1 |
0 |
1 |
0 |
P=q2p2=0.0406 |
12 |
1 |
0 |
1 |
1 |
P=qp3=0.0158 |
13 |
1 |
1 |
0 |
0 |
P=q2p2=0.0406 |
14 |
1 |
1 |
0 |
1 |
P=qp3=0.0158 |
15 |
1 |
1 |
1 |
0 |
P=qp3=0.0158 |
16 |
1 |
1 |
1 |
1 |
P=p4=0.0061 |
б) Располагаем в порядке убывания вероятностей и получаем кодовые слова:

1

 0,2687
0,2687
1
1
0,209

1
0
0,418
1
0,209
0
0,9996
0
1
1
0,5816
0
0,0812
1
0
0,1624
1
0,0812
0
0,3129
0
1
1
0
0,0812
0
1
0,1505

1
1
0
0,0316
0,0316
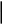
0
0,0377
0
1
0
0,0219
0
0
01
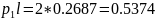
111
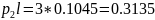
110
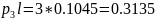
101
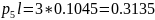
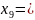 100
100
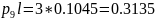
00111
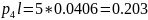
00110
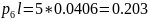
00101
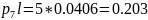
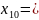 00100
00100
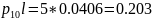
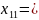 00011
00011
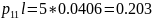
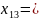 00010
00010
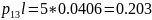
000001
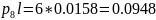
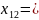 000011
000011
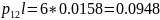
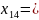 000010
000010
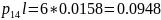
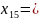 0000001
0000001
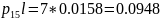
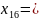 0000000
0000000
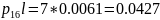
Средняя длина кодового слова:
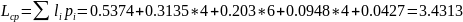
Расчёт придельных возможностей источника и сравнение с полученными результатами.
1) При n = 2:
Средняя длина кодового слова:
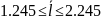
Кодирование по Шеннану-Фано:
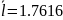
Кодирование по Хаффману:
Оба метода равноценны в данном случаи и удовлетворяют теоретической оценке средней границы.
2) При n = 3:
Средняя длина кодового слова:
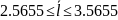
Кодирование по Шеннану-Фано:
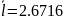
Кодирование по Хаффману:
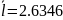
Оба метода равноценны в данном случаи и удовлетворяют теоретической оценке средней границы
4) При n = 4:
Средняя длина кодового слова:
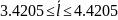
Кодирование по Шеннану-Фано:
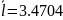
Кодирование по Хаффману:
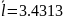
Метод Хаффмана более приближен к минимальной границе среднего значения длины кодового слова источника.
Вывод:
В ходе выполнения лабораторной работы можно сделать выводы:
При увеличении длины блоков длина кодовых слов увеличивается, что следует из подсчёта средней длины кодового слова. Также можно сказать, что эффективность повышается так как среднее значение приближается к нижней границе.
При увеличении энтропий источника оптимальность также повышается, потому что средняя длина также приближается к минимальной границе, которая была получена теоретическим путём.