ТП_23_ИСТ_1_1_Какушкина_Ольга_Витальевна_ЛР_4

МИНОБРНАУКИ РОССИИ

Ф едеральное государственное бюджетное образовательное учреждение высшего образования

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. Р.Е.АЛЕКСЕЕВА

Институт радиоэлектроники и информационных технологий

Кафедра информатики и систем управления

ОТЧЕТ по лабораторной работе №4

(наименование темы проекта или работы)

по дисциплине

Технологии программирования

(наименование дисциплины)

РУКОВОДИТЕЛЬ:

________________ Капранов С. Н.

(подпись) (фамилия, и.,о.)

СТУДЕНТ:

________________ Какушкина О.В

(подпись) (фамилия, и.,о.)

23-ИСТ-1-1

(шифр группы)

Работа защищена «___» ____________

С оценкой ________________________

Нижний Новгород 2025

ЦЕЛЬ РАБОТЫ: Изучение методов вычисления метрик программного кода.

Тема проекта: ПО «Распознавания аномалий на коже по фотографиям высокой четкости» 2-3 человека.

Задание: Используя задание проекта рассчитать метрики Хольстеда, Маккейба и Джилба для 3-4-х основных функций.

Первая функция

# Функция для создания модели def create_model(input_shape=(224, 224, 3)): base_model = ResNet50(weights='imagenet', include_top=False, input_shape=input_shape) x = base_model.output x = Flatten()(x) x = Dense(512, activation='relu')(x) x = Dropout(0.5)(x) predictions = Dense(1, activation='sigmoid')(x) model = Model(inputs=base_model.input, outputs=predictions) for layer in base_model.layers[-10:]: layer.trainable = True model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy']) model.summary() return model

Метрика Хольстеда:

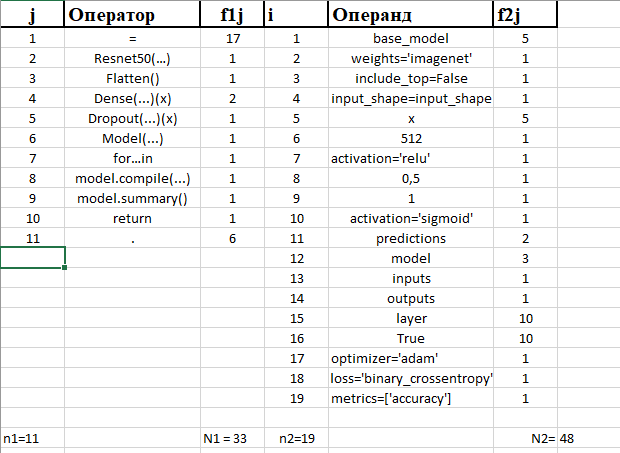
Рассчитаем словарь, длина и объем программы.

Словарь программы: n = 11 + 19 = 30.

Длина программы: N = 33 + 48 = 81.

Объем программы: V = 81 log₂ 30 = 397,45

Метрика МАККЕЙБА:

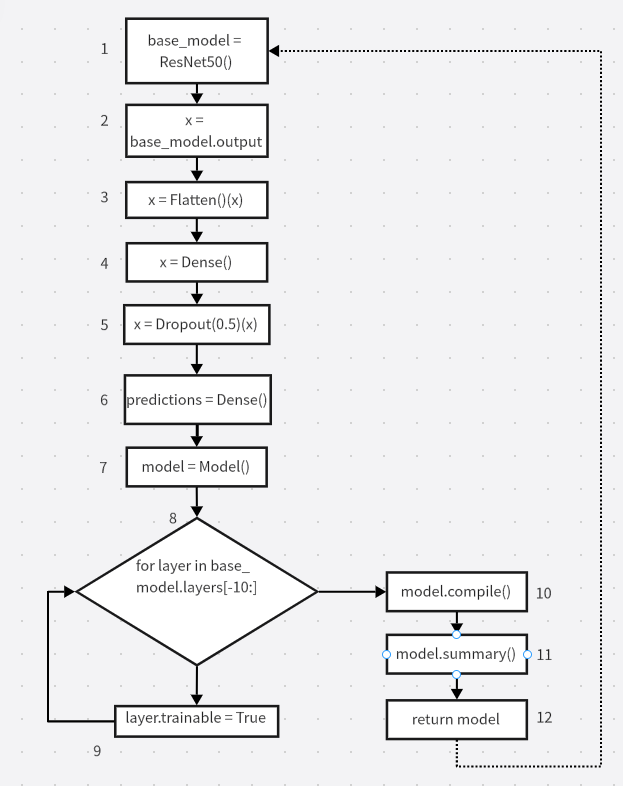
Метрика Маккейба определяет минимальное количество тестовых прого­нов программы, необходимых для тестирования всех ее ветвей.

Рассчитаем метрику Маккейба.

Компонент связности графа обозначен штриховой дугой.

Число дуг е = 12,

число вершин v = 12,

р = 1.

Цикломатическое число Маккейба равно Z(G) = 12 - 12 + 2 = 2.

Цикломатическая сложность для данного фрагмента кода составляет 2. Это означает, что в коде есть два линейно независимых пути, что указывает на относительно низкую сложность и легкость тестирования.

МЕТРИКИ ДЖИЛБА

Абсолютная сложность CL определяется количеством условных операторов и циклов.

CL=1

cl=CL​/n=1/11​≈0.09

Вторая функция

# Функция для записи результатов в JSON файл def log_result(image_path, pred_label, confidence_score): log_entry = { "image_path": image_path, "predicted_label": pred_label, "confidence_score": f"{confidence_score * 100:.1f}%", # Преобразуем в float "timestamp": datetime.now().strftime("%Y-%m-%d %H:%M:%S") } # Запись в JSON файл log_file = "results_log.json" # Если файл существует, загружаем существующие данные if os.path.exists(log_file): with open(log_file, "r") as f: try: data = json.load(f) # Загружаем данные except json.JSONDecodeError: # Обработка ошибки при неправильном формате JSON data = [] # Если ошибка, начинаем с пустого списка else: data = [] # Добавляем новую запись data.append(log_entry) # Сохраняем обновленные данные обратно в файл with open(log_file, "w") as f: json.dump(data, f, indent=4) # Преобразуем записи в строку и записываем в файл

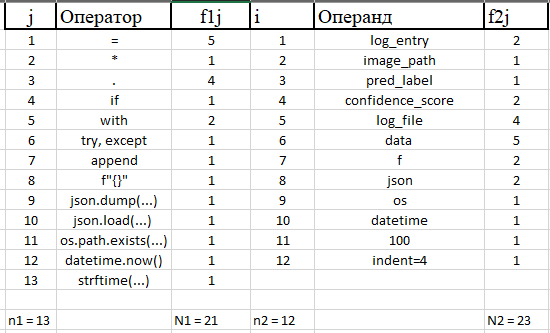
Рассчитаем словарь, длина и объем программы.

Словарь программы: n = 13 + 12 = 25.

Длина программы: N = 21 + 23 = 44.

Объем программы: V = 44 log₂ 25 = 204,3

Метрика МАККЕЙБА: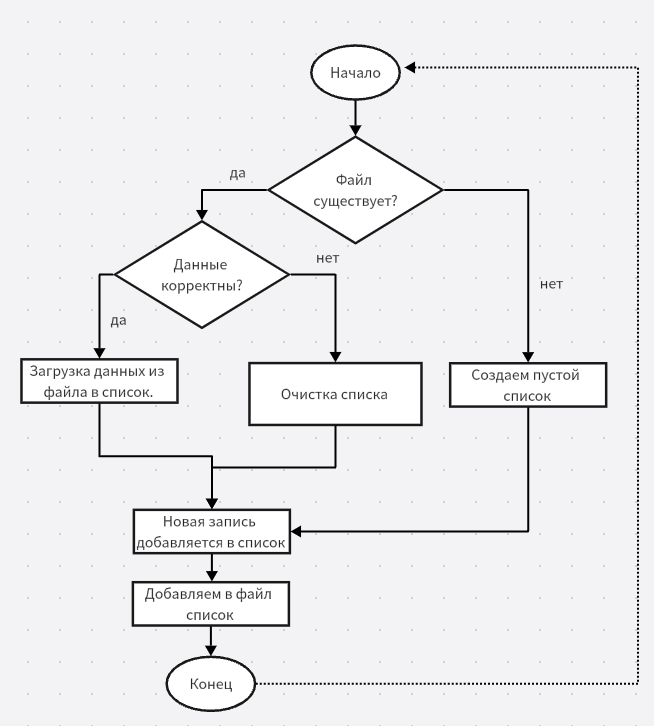

Компонент связности графа обозначен штриховой дугой.

Число дуг е = 10,

число вершин v = 9,

р = 1.

Цикломатическое число Маккейба равно Z(G) = 10 - 9 + 2 = 3.

Цикломатическая сложность для данного фрагмента кода составляет 3. Это означает, что в коде есть три линейно независимых пути, что указывает на относительно низкую сложность и легкость тестирования.

МЕТРИКИ ДЖИЛБА

Абсолютная сложность CL определяется количеством условных операторов и циклов.

CL=1 (блок try, except не учитываем как условный оператор в данной метрике)

cl=CL​/n=1/13​≈0.077

Третья функция

def visualize_predictions(model, test_generator, label_dict): x_test, y_test = next(test_generator) y_pred = model.predict(x_test) y_pred_classes = (y_pred > 0.5).astype("int32") y_true_classes = y_test fig, axes = plt.subplots(nrows=1, ncols=len(x_test), figsize=(12, 6)) for i, ax in enumerate(axes.flat): ax.imshow(x_test[i]) pred_label = label_dict[y_pred_classes[i]] true_label = label_dict[y_true_classes[i]] print(f"Image {i + 1}: Predicted Class: {pred_label}, True Class: {true_label}") ax.set_title("Pred: {}\nTrue: {}".format(pred_label, true_label)) ax.axis('off') plt.tight_layout() plt.show()

Метрика Хольстеда:

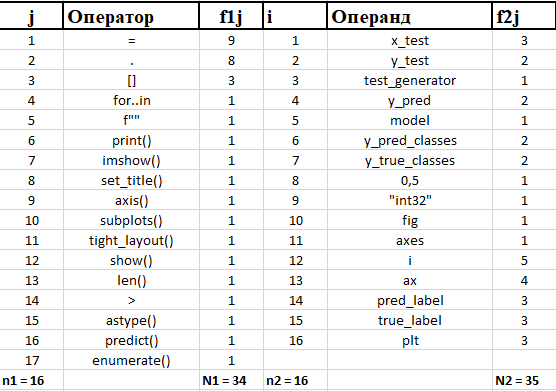
Рассчитаем словарь, длина и объем программы.

Словарь программы: n = 17 + 16 = 33.

Длина программы: N = 34 + 35 = 69.

Объем программы: V = 69 log₂ 33 = 348,06

Метрика МАККЕЙБА:

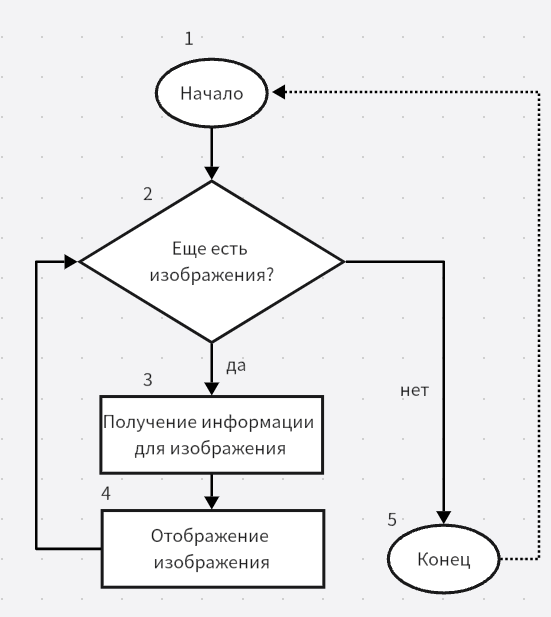
Число дуг е = 5,

число вершин v = 5,

р = 1.

Цикломатическое число Маккейба равно Z(G) = 5 - 5 + 2 = 2.

МЕТРИКИ ДЖИЛБА

Абсолютная сложность CL определяется количеством условных операторов и циклов.

CL=1

cl=CL​/n=1/17​≈0.059

Вывод: в ходе выполнения лабораторной работы были изучены подходы к вычислению метрик программного кода. По результатам вычислений первая функция имеет наибольшее значение объема программы по Хольстеду и наибольшую абсолютную сложность по Джилба. Вторая функция имеет наибольшее число линейно независимых путей.