Чистый сдвиг (срез)
Если на гранях выделенного элемента действует только касательное напряжение, то говорят что элемент конструкции испытывает деформацию чистого сдвига или среза. На практике испытывают валиковые сварные швы, заклепки и болты поставленные в отверстие без зазора и т.д.
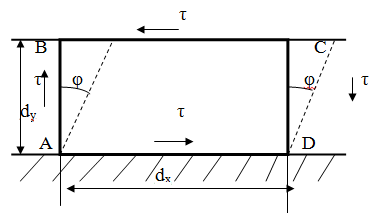
Рисунок 16
сторона АД – защемлена;
а = ВВ/ = СС/ - абсолютная деформация сдвига;
γ – угол сдвига или угловая деформация при сдвиге;
г) τ- касательное напряжение.
γ
lg·
γ =
Опытным путем Гук установил следующую зависимость между и напряжением, которая появляется при сдвиге.
γ =
- закон Гука при сдвиге или срезе;
- закон Гука при растяжении;
где а) G – модуль упругости 2 раза или модуль упругости при сдвиге (G, );
б)
ε,
G
– являются физической характеристикой
материала, показывает способность
материала сопротивляться деформациям
сдвига (дается в справочнике), если нет
справочника, то:
;
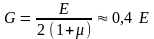в) - модуль упругости 1 рода;
г) μ - коэффициент Пуассона.
Практические расчеты на срез Расчет заклепочных соединений на срез
Рисунок 17
где Q – поперечная сила.
Предполагают, что при срезе напряжение распределяется по сечению заклепки равномерно.
Уравнение равновесия отсеченной части соединения, например нижней.
=
Условие прочности на срез:
;
где
а)
- фактическое напряжение среза;
б) F – срезывающая сила;
в) d – диаметр заклепки;
г)
[
]
- допускаемое напряжение на срез материала
заклепки (в справочнике);
д) n – число заклепок в одном ряду;
е) i – количество плоскостей среза заклепки.
Расчет заклепок на смятие
Деформация смятия представляет собой деформацию сжатия по плоскостям передачи сил давления от одного элемента конструкции к другому.
- напряжение при
смятии:
а·
=А
см – площадь
смятия
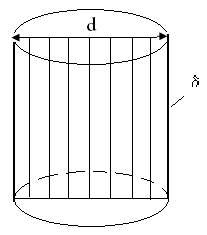
Рисунок 18
Кручение
Кручение испытывает валы. M1=M2
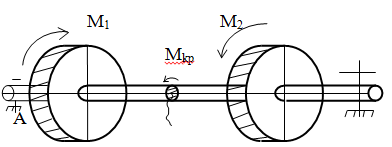
Рисунок 19
Участок вала между шкивами под действием внешних вращательных моментов М1 и М2 будет испытывать деформацию кручения. Внешние моменты будут называться скручивающими моментами.
Крутящий момент представляет собой равнодействующую всех внутренних усилий, лежит на плоскости поперечного сечения вала и определяется методом сечения.
Крутящий момент = алгебраической сумме скручивающих моментов, действующих по одну сторону от рассматриваемого сечения.
Правило знаков: крутящийся момент положительный, если скручивающий момент напряжения по ходу часовой стрелки при взгляде со стороны сечения.
Рисунок
Mkp>0 Mkp<0
Отрицательный, если скручивающий момент против хода часовой стрелки.
Для наглядного изображения закона изменения крутящий момент по длине вала строят эпюру крутящих моментов.
При делении на участки границами являются те сечения, где приложены внешние скручивающие моменты.
Определение напряжения при деформации кручения круглых стержней.
Допущение:
1. сечение плоское до деформации кручения остается плоским и после деформации кручения. Они лишь поворачиваются друг относительно друга;
2. расстояние между поперечным сечением при деформации кручения не меняются;
3 . радиусы поперечного сечения не искривляются.
Р
исунок x dx l M
C1 D1
B1 x
A B C D
I II
Стержень одним концом заделан и нагружен вращающим моментом М. Проведем образующую АД, которая под действием момента займет положение АД.
Выделим элемент длиной dх между 2 - мя сечениями. Образующая этого элемента ВС перейдет в положение В/С/, отклонившись на угол
=
=
Угол
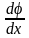- это угол закручивания на единицу длины
стержня, он называется относительным
углом закручивания
.
= r
Закон Гука при сдвиге:
;
- касательное
напряжение.
Отсюда можно
определить напряжение по величине
относительно сдвига в окрестности любой
точки тела, находящейся на расстоянии
от оси.
G – модуль упругости при сдвиге.
Р исунок
φ
ρ
C
= GΘ
,
т.е. значения касательных напряжений в точках сечения пропорциональны расстоянию их от оси стержня.
Значение можно найти из условия, что касательные напряжения в сечении приводятся к паре, момент которой равен крутящему моменту Мкр.
Выделим вокруг
произвольной точки сечения элементарную
площадку dA,
на которую будет действовать элементарная
окружная сила
.
Элементарный момент этой силы относительно оси стержня
dMкр
=
суммируя элементарные площадки, найдем крутящий момент в сечении.
;
где: Iр – полярный момент инерции сечения.
Таким образом, получаем:
,
откуда угол закручивания будет равным
;
Произведение
- называется жесткостью стержня при
кручении.
Определим зависимость напряжения от крутящего момента:
,
отсюда наибольшее напряжение при кручении
Эпюра изменения напряжения по сечению
Р исунок Mkp
τmax
D=2r
При
= r,
- полярный момент
сопротивления сечения.
- для круглого
поперечного сечения.
- условия прочности
при кручение.
- формула
проектировочного расчета.
Определение деформации при кручении
Мерой деформации при кручении является относительный угол закручивания угол поворота, приходящийся на единицу длины:
;
где: а)
– угол поворота;
б)
- длина между сечениями.
=
=
=
=
=
- для стержней переменного поперечного
сечения с изменением крутящего момента.
Величина поворота алгебраической сумме углов поворотов отдельных участков.
Расчет на прочность и на жесткость при кручении
1) Условие прочности
Вал будет прочный
если
Для проектировочного расчета используется следующая формула:
2) Условие жесткости
- допускаемый угол
закручивания, который определяется
опытным путем и приводится в справочнике.
Поперечный изгиб
Часто стержни подвергаются действию поперечной нагрузки или внешних пар. При этом в поперечных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.
При действии таких нагрузок ось стержня искривляется.
Этот вид нагружения называют изгибом, стержни, работающие на изгиб – балками.
Изгиб называют чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня. Если в поперечных сечениях наряду с изгибающими моментами появляются, также поперечные силы изгиб называют поперечным.
Р исунок F M1 M2
A B z
F
Изгиб бывает: 1) прямым; 2) косым.
1). Прямой или плоский поперечный изгиб – если все силы вызывающие деформацию изгиба лежат на одной из главных плоскостей балки.
Главной плоскостью балки называется плоскость, проходящая через продольную ось балки и через одну из центральных осей поперечного сечения балки, центральной осью поперечного сечения балки называется ось относительно которой статический момент сечения = 0 (т.е. оси симметрии).
2) Косой поперечный изгиб бывает плоский и пространственный.
При плоском косом изгибе все силы вызывающие деформацию изгиба лежат на одной плоскости, не совпадающей ни с одной главной плоскостью балки.
Р
исунок y
q
α m
F m x Q
При простом косом изгибе силы вызывающие деформацию изгиба лежат на разных плоскостях.
Прямой поперечный изгиб
Определение внутренних усилий при прямом поперечном изгибе
Все внутренние силы, возникающие в рассматриваемом поперечном сечении при изгибе проводятся к одной силе, лежащей в плоскости поперечного сечения балки Q, называемой поперечной силой и к одному моменту Ми лежащего в плоскости действия внешних сил, называемому изгибающим моментом.
Для определения Q и Ми применяется метод сечения.
Рисунок
y F1 Q F2
Ra Mизг 0 Rb z
А a a a В
1.
Поперечная сила рассматриваемого сечения равна сумме проекций всех сил действующих по одну сторону от рассматриваемого сечения на ось y.
Правила знаков для Q:
Положительный, если результирующая сила слева от сечения направлена снизу вверх, а справа от сечения сверху вниз.
Отрицательный, если результирующая сила слева от сечения направлена сверху вниз, а справа от сечения снизу вверх.
Рисунок
0 0
Q>0 Q<0
0 – центр тяжести сечения.
2.
=
Ми
=
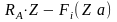
Ми
=
Ми = сумме моментов всех сил действующих на оставшуюся часть балки по одну сторону от рассматриваемого сечения относительно центра тяжести данного сечения.
Правило знаков:
положительный, если равнодействующий момент слева от сечения направлен по ходу часовой стрелки;
отрицательный, если момент слева от сечения против хода, справа по ходу часовой стрелки.
Рисунок
Mизг>0 Mизг<0
Q и Ми. по длине балки непостоянны. Для наглядного изображения закона изменение поперечной силы и изгибающего момента по длине балки строят эпюры Q и Ми.
Основные правила построения эпюры Q и Ми
Для эпюра Q:
1) на участках нагруженных распределенной силой q эп.Q изображается прямой, наклонной к оси балки угол наклона зависит от интенсивности распределения нагрузки;
2) на участках свободных от распределенной силы q эп.Q изображается прямыми параллельными оси балки;
3) под сечениями балки, где приложены сосредоточенные силы эп.Q имеются скачки равные величинам приложенных сил;
4) в сечениях, где приложены сосредоточенные пары сил, поперечная сила не меняет своего значения.
Для эп.Ми:
1) на участках нагруженных распределенной нагрузкой q эп. Ми: изображается квадратной параболой, выпуклость параболы направлена в сторону противоположную действию нагрузки;
2) на участках нагруженных сосредоточенными силами эп. Ми изображается ломаными линиями с вершинами под точкой приложения сосредоточенных сил;
3) под сечениями балки, где приложены сосредоточенные пары сил эп. Ми имеются скачки равные моменту этих пар сил;
4) изгибающий момент в концевых сечениях балок равен 0, если в этих сечениях не приложены сосредоточенные пары сил, если в конце сечения приложены сосредоточенные пары сил, то изгибающий момент в этих сечениях равен по величине момента приложенных пар;
5) сопряжение параболической части эп. Ми с прямолинейной частью происходит плавно, если в сечениях, где кончается или начинается q, к балке не приложена сосредоточенная сила;
6) изгибающий момент достигает max или min в тех сечениях балки, в которых поперечная сила равна 0.
Определение нормальных напряжений при прямом поперечном изгибе
При прямом поперечном изгибе возникают и касательное и нормальное напряжение в каждой точке балки. По величине касательное напряжение на много меньше нормального.
Поперечная сила вызывает касательное напряжение.
Изгибающий момент вызывает нормальное напряжение, которое перпендикулярно к плоскости поперечного сечения.
При расчетах на прочность при прямом поперечном изгибе рассчитывается только нормальное напряжение, а касательное - нет.
Если подвергнуть чистому плоскому изгибу балку с нанесенной на ее поверхности сеткой, то обнаружится следующее .
Линии
-
,
-
на поверхности балки повернутся на
некоторый угол
,
оставаясь прямым.
Расстояние
- не изменяется.
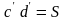
При деформации изгиба слои балки, лежащие на выпуклой стороне, испытывают деформацию растяжения, а на выгнутой – сжатия.
А слой волокон по
линии
- не деформируются.
Слой волокон, который не деформируется - называется нейтральным слоем.
Ось Z – нейтральная ось.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения балки – называется нейтральной осью.
Сечение плоское до деформации изгиба остается плоской и после деформации изгиба, они лишь поворачиваются на некоторый угол вокруг нейтральной оси, оставаясь перпендикулярными к изогнутой оси балки.
При изгибе продольные слои волокон не давят друг на друга. Они испытывают либо линейное растяжение, либо линейное сжатие.
- абсолютная
деформация.
- относительная
деформация.
где: а) y – расстояние от рассматриваемого слоя до нейтрального;
б) - радиус кривизны.
По закону Гука:
,
отсюда найдем (
)
или выразив
- кривизна балки.
Возьмем в сечении
элемент dA
или
Отсюда через изгибающий момент определим напряжение в любой точке сечения.
;
где: а) Ми, Ix – const;
б) зависит от y.
когда y = 0; = 0
Нарисуем эпюру изменения изгиба по сечению балки.
(выпуклая)
Рисунок σcmax
σpmax
(выгнутая)
Если сечение симметрично относительно нейтральной оси, вводится понятие осевого момента сопротивления - Wx
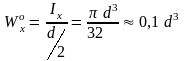
Для круглого сечения:
Если балка имеет двутавровое сечение, то найдем по ГОСТу:
Условие прочности при прямом поперечном изгибе
Фактически max напряжение изгиба:
Условие прочности при изгибе.
Опасное то сечение, где поперечное сечение меньше, и где max изгибающий момент.
Если площадь поперечного сечения меняется, то опасное сечение там, где Wx – имеет наименьшее значение, и где Ми – имеет наибольшее значение.
- зависит только
от материала.
При проектировочном расчете:
