
- •Общие положения
- •Метод сечений
- •Понятие о напряжениях
- •Понятие о деформации
- •Центральное растяжение (сжатие)
- •Механические характеристики материалов и диаграмма растяжения
- •Определение допускаемых напряжений
- •Расчеты на прочность при центральном растяжении (сжатии)
- •Геометрические характеристики плоских сечений
- •1. Статический момент сечения (площади поперечного сечения)
- •Чистый сдвиг (срез)
- •Практические расчеты на срез Расчет заклепочных соединений на срез
- •Расчет заклепок на смятие
- •Кручение
Общие положения
Любая конструкция (машина, постройка) должна выдерживать нагрузки, иногда очень значительные, при сохранении формы и размеров отдельных элементов.
В теоретической механике тела считается абсолютно твердыми, на самом деле под действием внешних сил все твердые тела деформируются.
Под действием внешних сил в элементах конструкции могут возникать упругие деформации, а также и остаточные (пластические) деформации, возникновение которых может привести к нарушению нормальной работы конструкции, что недопустимо.
Способность конструкции (или отдельного её элемента) выдерживать заданную нагрузку не разрушаясь и без появления остаточных деформаций, называется прочностью.
Способность конструкции (или отдельного её элемента) сопротивляться упругим деформациям называется жесткостью.
Способность конструкции (или отдельного её элемента) сохранять первоначальную форму упругого равновесия называется устойчивостью.
Метод сечений
Способность тела сопротивляться изменению первоначальной формы определяется силами сцепления между всеми смежными частицами тела, которые в отличие от внешних сил, приложенных к телу, называется внутренними силами.
Внутренние силы – силы межатомного взаимодействия, возникающие при воздействии на тело внешних нагрузок.
Расчет конструкции на прочность или жесткость – это определение внутренних сил по заданной нагрузке.
Внутренние силы определяют прочностную надежность детали.
Для определения внутренних сил применяется метод сечения.
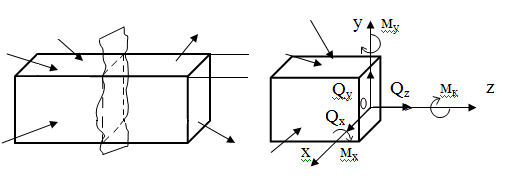
Рисунок 1

 ,
,
 ,
,
 ,Mx,
My,
Mz,
‒
внутренние
силовые факторы;
,Mx,
My,
Mz,
‒
внутренние
силовые факторы;
где а) N – нормальная (продольная) сила;
б) Qx, Qy – поперечные силы;
в) Mk – крутящий момент;
г) Mx, My ‒ изгибающие моменты, которые определяются из уравнения равновесия:
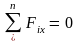
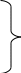
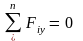
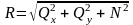
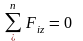
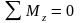
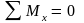
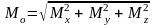
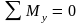
Понятие о напряжениях
В сечении в окрестности точки К выделим элементарную площадку А, тогда среднее давление определится:
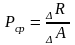 ,
,
где а) R - равнодействующая внутренних сил, действующая на элементарную площадь;
б) А - площадь площадки.
p=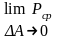 =
=
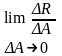
[p]
=
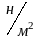 =
Па
=
Па
1мПа = 106
Па = 1
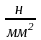
Напряжением
называется внутренняя сила, приходящаяся
на единицу площади. Вектор
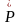 можно разложить в точке сечения, на 2
составляющие.
можно разложить в точке сечения, на 2
составляющие.
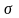 – нормальное
напряжение;
– нормальное
напряжение;
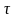 - касательное
напряжение.
- касательное
напряжение.

Рисунок 2
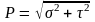
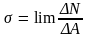 ,
где
,
где
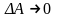
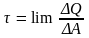 ,
где
,
где
ху=
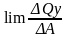 ,
где
,
где
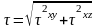
хz=
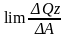 ,
где
,
где
Понятие о деформации

Рисунок 3
Различные линейные и угловые деформации.
dx, dy ‒ абсолютные деформации по отношению x и y; (м);
γ ‒ угловая деформация (рад.);
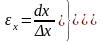 ‒ относительная
деформация
‒ относительная
деформация
Если после снятия внешней нагрузки тело принимает прежний вид, то говорят, что тело испытывает упругую нагрузку, если не принимает свою форму, то это – остаточная деформация, пластичность.
Центральное растяжение (сжатие)
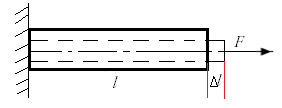

Рисунок 4
Тело испытывает деформацию растяжения.
Вид деформации, при котором в поперечном сечении появляются продольные внутренние силы, называется центральным растяжением (сжатием).
а) Определение внутренних усилий.
Применяется метод сечения

Рисунок 5
N – продольная сила находится из уравнения
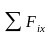 =
F-N
= 0
=
F-N
= 0 N=F
N=F
Принято положительную растягивающую продольную силу направлять от сечения, сжимающую отрицательную к сечению.
Для наглядного изображения закона распределения продольных сил строят эпюру продольных сил.
б) Определение напряжения при центральном растяжении (сжатии).
Формулы для определения напряжений получены на основании гипотезы плоских сечений (гип. Бернулли). Поперечные сечения стержня плоские и нормальные к его оси до деформации, останутся таковыми и после деформации, т.е. можно считать, что в поперечных сечениях стержня действуют только нормальные напряжения.

Рисунок 6
Напряжение растяжения по сечению распространяется равномерно.
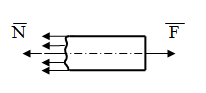
Рисунок 7
N= A
p(c)=N/A
в) Определение деформации.
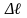 ‒ абсолютная
деформация при растяжении (сжатии), [м].
‒ абсолютная
деформация при растяжении (сжатии), [м].
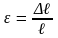 ‒ относительная
продольная деформация.
‒ относительная
продольная деформация.
В 1660 г Гук вывел: линейные деформации пропорциональны нормальным напряжениям.
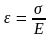 ‒ закон Гука,
‒ закон Гука,
где
а)
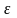 - относительная деформация;
- относительная деформация;
б) ‒ направление растяжение (сжатие);
в)
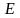 - [
- [ ]
– модуль упругости при растяжении
(сжатии), т.е. характеризует способность
материалов сопротивляться к деформации
растяжения (сжатия), (в справочнике).
]
– модуль упругости при растяжении
(сжатии), т.е. характеризует способность
материалов сопротивляться к деформации
растяжения (сжатия), (в справочнике).
Тогда:
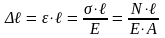 ‒ закон Гука, для
тех участков, у которых N,
E,
A
= const.
‒ закон Гука, для
тех участков, у которых N,
E,
A
= const.
Произведение
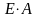 определяет
жесткость.
определяет
жесткость.
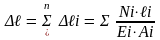
Для наглядного изображения закона изменения продольных деформаций по длине стержня строят эпюру продольных деформаций.
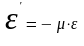
где а)
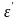 - поперечная деформация;
- поперечная деформация;
б)
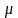 - коэффициент Пуассона (берется из
справочника);
- коэффициент Пуассона (берется из
справочника);
в) - продольная деформация.
