Равновесие при наличии сил трения.

При стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному движению, называемая силой трения скольжения (причины: шероховатость поверхности, наличие сцепления у прижатых друг к другу тел).

Законы трения скольжения.

1) При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения ( или сила сцепления), величина которой может принимать любые значения от нуля до значения F_пред (F_пр), называемого предельной силой трения.

Сила трения направлена в сторону, противоположную той, куда действующая сила стремятся сдвинуть тело.

2) Величина предельной силы трения равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию.

-число отвлеченное, определяется опытным путем и зависит от материала поверхностей и состояния их.

3) Величина предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся при трении поверхностей.

Объединяя вместе 1 и 2 законы трения, получим, что при равновесии сила трения покоя

или

Экспериментальное определение коэффициента трения.

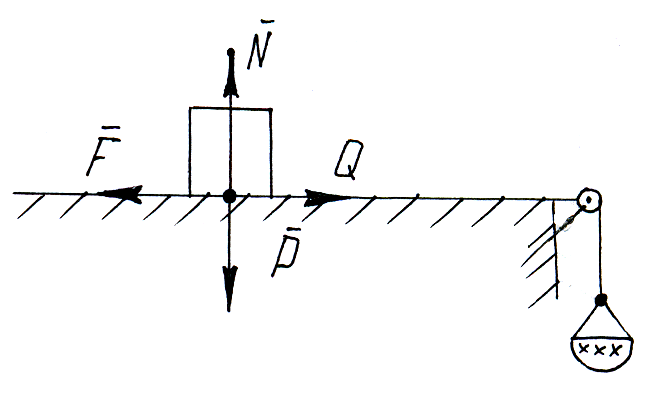
Р авновесие под действием

.

Увеличивая Q (добавляя груз) найдем ту нагрузку, при которой брусок сдвинется с места Q^*.

Очевидно, что .

Все изложенное выше относится к трению скольжению при покое.

При движении сила трения направлена в сторону, противоположную движению, и равна произведению динамического коэффициента трения на нормальное давление

( зависит как и , а также и от скорости движения)

Реакции шероховатых связей. Угол трения.

F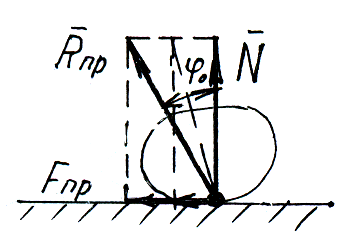 _тр меняется от 0 до F_пр.

R меняется от N до R_пр.

Угол растет от 0 до φ₀.

Наибольший угол, который полная реакция шероховатой связи образует с нормалью и поверхностью, называется углом трения.

Из чертежа , т.к. , то получим: .

При равновесии полная реакция в зависимости от сдвигающих сил будет находиться где угодно внутри угла трения.

Т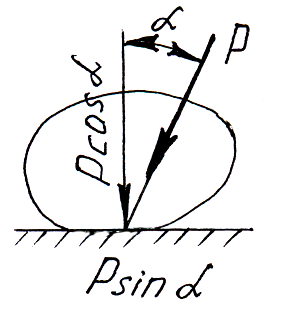 ело сдвинется только тогда, когда сдвигающее усилие будет больше (считаем, что , весом тела пренебрегаем).

т.е.

Следовательно, никакой силой, образующей с нормалью угол , меньший угла трения , тело вдоль данной поверхности сдвинуть нельзя.

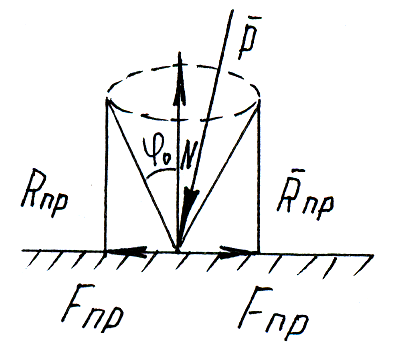
Конус трения – конус с вершиной в точке касания тел, образующая которого составляет с нормалью угол трения. Поверхность конуса трения представляет собой геометрическое место предельных реакций .

Равновесие при наличии трения.

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наибольшего значения .

Реакция и .

Составляют обычные уравнения равновесия и решают их.

Расчет ферм.

Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция.

Если оси всех стержней лежат в одной плоскости, то такую ферму называют плоской.

А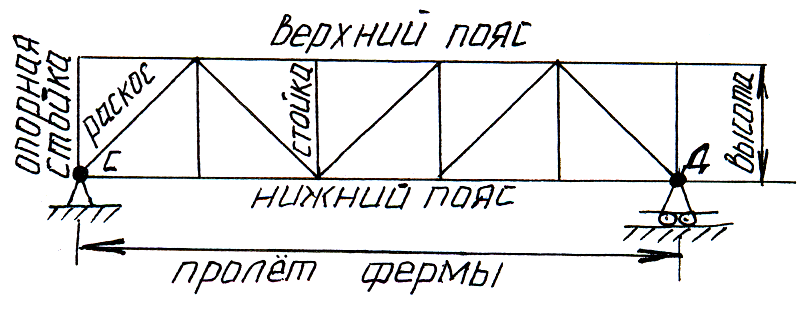 ,В-узлы фермы

С,D-опорные узлы

Все шарниры, соединяющие стержни фермы предполагаются идеальными, т.е. без трения, а все внешние силы – приложенными в узлах фермы, т.е. все стержни испытывают лишь растяжение или сжатие (вес стержней не учитывают).

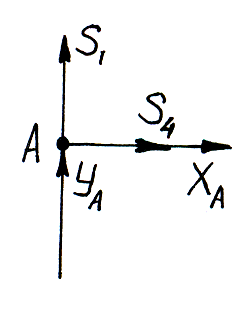
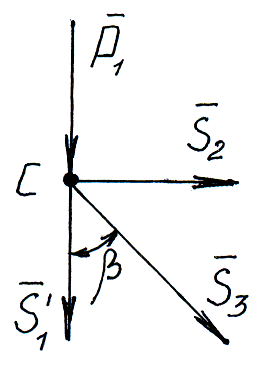
1 способ расчета ферм – (определение опорных реакций и усилий - способ вырезания узлов в стержнях).

Этот способ сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние реакции и реакции стержней и составляют уравнения равновесия сил, приложенных к каждому узлу. Условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов).

Если в вычислениях получается знак «–», то соответствующий стержень сжат.

Найденные реакции стержней равны по модулям внутренним усилиям в стержнях.

Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу не должно превышать число уравнений равновесия.

П ример:

Определим реакции опор:

2 способ расчета ферм: метод Риттера (метод сечений).

Ф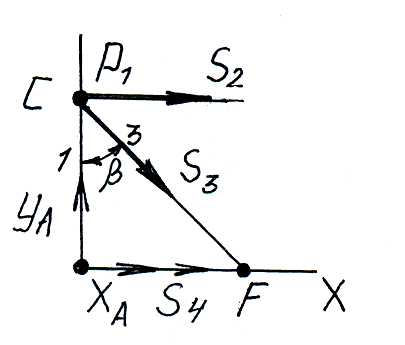 ерму мысленно разделяют на 2 части сечением и рассматривают равновесие одной из частей (сечение проводят так, чтобы число неизвестных не превышало трех). Действие отброшенной части заменяют силами – реакциями соответствующих стержней, направляя их вдоль стержней от узла, т.е. считая стержни растянутыми.

Метод Риттера удобно использовать для проверочных расчетов.

Лекция 9.