Равновесие пространственной параллельной системы сил.

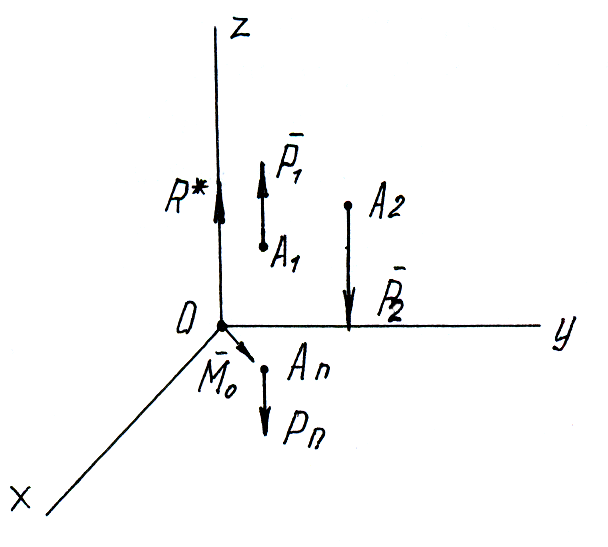
Система параллельных сил , приложенных в точках .

и .

Вычислим проекции на эти оси:

направлен по оси OZ, а его модуль равен абсолютному значению его проекции Z.

Вычислим

Проекции главного момента относительно начала координат на оси x,y,z, как главные моменты сил относительно этих осей.

Т.к. силы параллельны OZ, то и лежит в плоскости XOY.

Запишем условия равновесия параллельной системы сил.

, (геометрическое условие равновесия)

, , (аналитическое условие равновесия)

Распределенные силы.

В статике рассматриваются силы, приложенные в одной точке – так называемые сосредоточенные силы. В действительности силы обычно бывают приложены к какой-либо части объема тела или к его поверхности или линии, которые называют распределенными силами. Т.к. аксиомы и теоремы статики формулируются для сосредоточенных сил, необходимо знать способы перехода от распределенных сил к сосредоточенным.

Распределенные силы характеризуются интенсивностью, т.е. силой приходящейся на единицу объема, площади или длины.

Параллельные силы постоянной интенсивности.

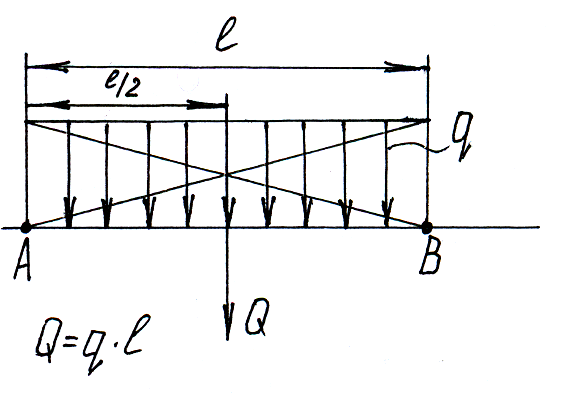
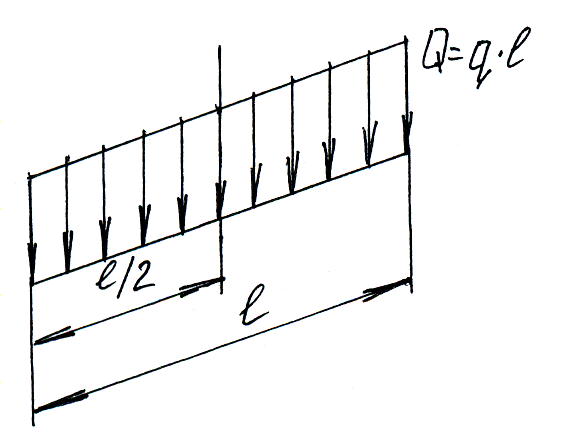
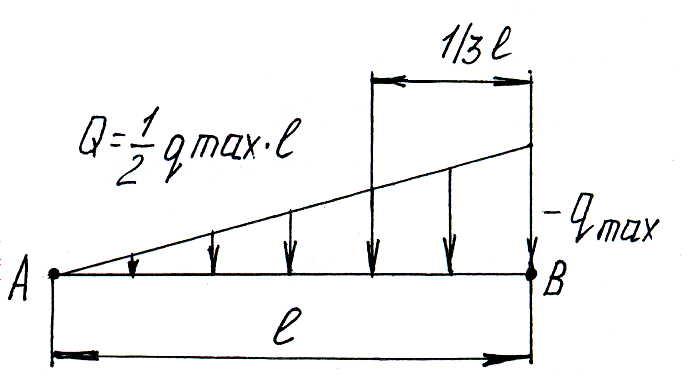
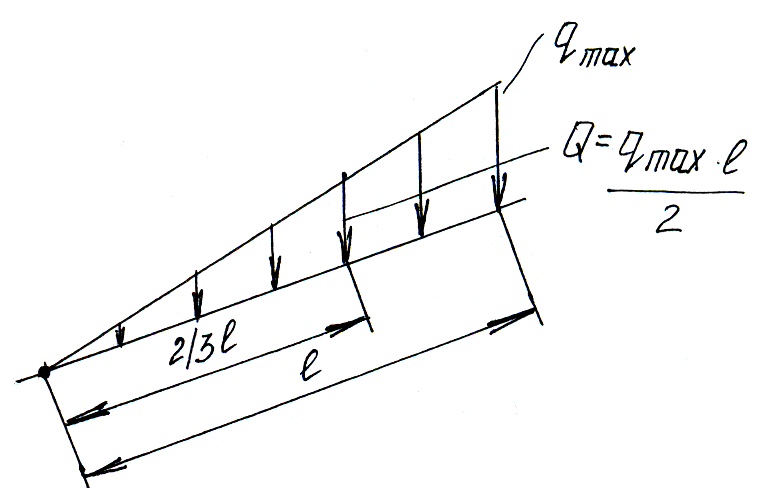
Параллельные силы с интенсивность, изменяющейся по линейному закону.

Теорема о моменте равнодействующей силы (теорема Вариньона).

Т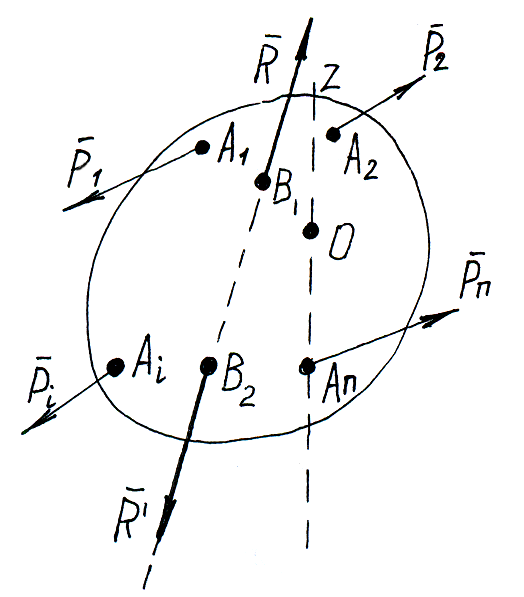 еорема: момент равнодействующей системы сил относительно любой точки равен геометрической сумме моментов всех сил этой системы относительно той же точки. Момент равнодействующей силы относительно произвольной оси равен алгебраической сумме моментов сил системы относительно той же оси.

Н а твердое тело действует произвольная система сил , имеющая равнодействующую силу , т.е. .

К заданной системе сил добавим ее уравновешивающую силу .

0.

Получим в результате систему эквивалентную нулю, следовательно, можно записать условия равновесия, в частности, геометрическая сумма моментов сил этой новой системы относительно любой точки О равен нулю.

,

но ,

получим

Если правую и левую часть этого выражения спроектировать на произвольную ось OZ, получим

Статически определенные и статически неопределенные задачи.

Статически определенными называют задачи, которые можно решать методами статики твердого тела, т.е. задачи, в которых число неизвестных не превышает числа уравнений равновесия сил.

Статически неопределенными называют задачи с числом неизвестных, превышающим число уравнений равновесия сил.

Равновесие системы соединенных тел.

К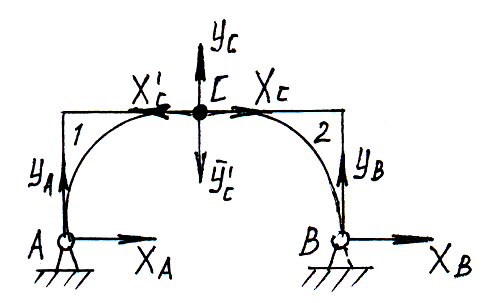 онструкция – система тел, соединенных какими-нибудь связями.

Связи, соединяющие части данной конструкции, будем называть внутренними.

Связи, соединяющие конструкцию с другими телами, будем называть внешние.

Данная задача является статически неопределенной (4 неизвестных, а уравнений 3).

Поэтому отбрасываются не только внешние, но и внутренние связи, причем реакции внутренней связи – шарнира С, приложенные к телам 1 и 2, попарно равны по модулям и противоположны по направлению, т.к. выражают действие и противодействие.

Можно рассмотреть равновесие: 1) системы и равновесие 1первого тела;

2) равновесие первого и второго тела по отдельности.

Получим 6 уравнений, т.е. задача будет статически определенной.

Лекция 8.