Вычисление главного вектора и главного момента системы сил п роизвольно расположенных на плоскости.

Воспользуемся методом проекций.

, т.О - центр приведения

X, Y – проекции главного вектора на оси координат.

, где Y₁,Y₂,Y₃ и X₁,X₂,X₃-проекции сил на координатные оси.

Модуль и направление главного вектора определяются:

Все присоединенные пары сил лежат в одной плоскости.

– алгебраическая сумма моментов всех сил системы относительно центра приведения.

Уравнения равновесия системы сил, произвольно расположенной в плоскости.

Если главный вектор системы сил и главный момент относительно центра приведения равны нулю, то силы взаимно уравновешиваются.

Можно записать:

Основные уравнения равновесия плоской системы сил:

Существуют и две другие системы уравнений равновесия сил:

1) . Ось U не должна быть перпендикулярно прямой, проходящей через т.А и т.В.

2) . т.А,В,С не должны лежать на одной прямой.

У равнения равновесия параллельных сил.

Дана система параллельных сил: . Точки приложения: А₁,А₂…А_n.

Приведем силы к произвольному центру О. Получим и . Вычислим проекции на координатной оси.

,

т.к. X=0, то главный вектор направлен по оси OY

Главный вектор системы параллельных сил параллелен силам, его модуль равен абсолютному значению алгебраической суммы проекции сил на ось, параллельную силам, а его направление определяется знаком этой суммы.

Для системы параллельных сил на плоскости имеем 2 условия равновесия:

1) ; - основное уравнение равновесия параллельных сил на плоскости (центр О выбран произвольно).

2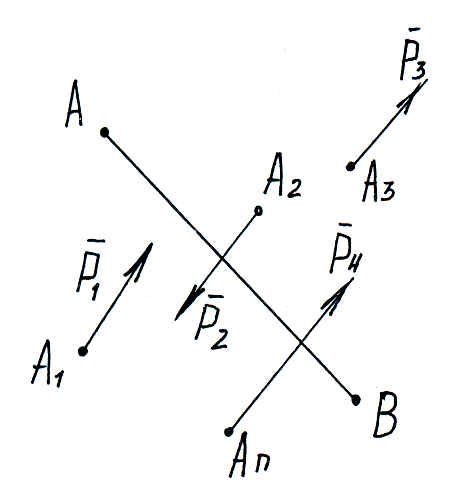 ) ; - ограничение: прямая АВ не должна быть параллельна силам.

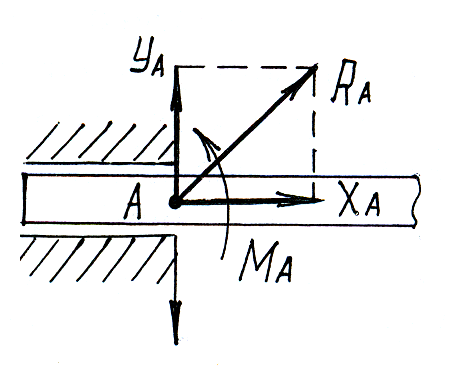« Глухая заделка» («жесткая заделка»).

На заделанный конец балки со стороны опорных плоскостей действует система распределенных сил реакций. Приводим их к центру А, заменив неизвестной и . Надо определить: X_A,Y_A,M_A.

Лекция 6.

Главный вектор и главный момент произвольной пространственной системы сил.

Знаем, что произвольная система сил может быть приведена к одной силе, равной главному вектору системы относительно центра приведения и приложенной в центре приведения и паре сил с моментом, равным главному моменту системы относительно центра приведения.

X,Y,Z-проекции главного вектора

X₁…X_n, Y₁…Y_n, Z₁…Z_n-проекции сил на координатные оси

Модуль и направление главного вектора:

Модуль и направление главного момента.

Условие равновесия произвольной пространственной системы сил.

Необходимо и достаточно, чтобы одновременно , .

Но векторы и будут равны нулю, если будут равны нулю все проекции на оси координат, т.е.

Таким образом для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

Первые три уравнения выражают необходимые условия того, чтобы тело не имело перемещений вдоль координатных осей, а последние три являются условием отсутствия вращения вокруг этих осей.