Сложение пар сил.

Система пар, действующих на твердое тело, эквивалентна одной паре, момент которой равен геометрической сумме моментов этих пар.

Д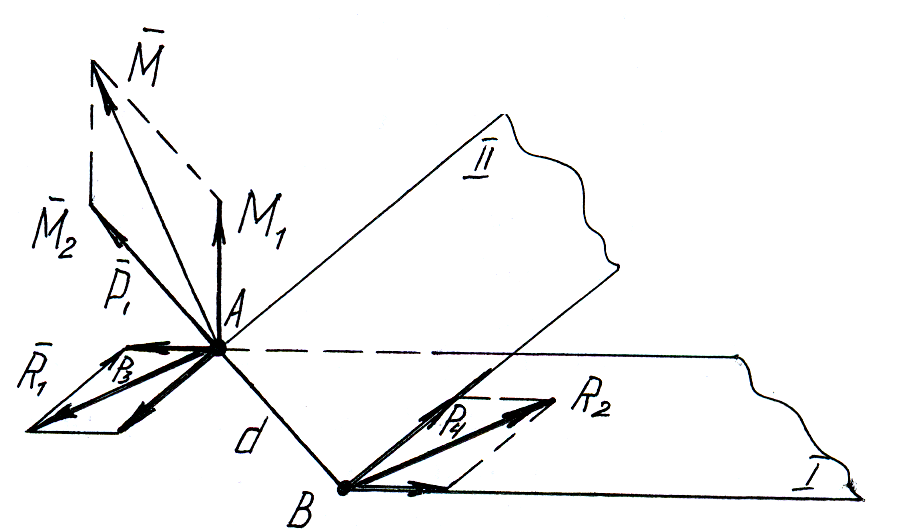 окажем это для 3 пар. Даны 2 пары сил с моментами и , лежащие в плоскостях I и II.

АВ – прямая пересечения плоскостей I и II.

АВ=d

момент

момент .

.

пары заменяются одной парой

Найдем момент равнодействующий .

но а

Следовательно:

Если n пар, то

Если же пары лежат водной плоскости, то эта система пар эквивалентна паре, лежащей в той же плоскости и момент её равен алгебраической сумме моментов этих пар.

Условия равновесия пар сил.

Для равновесия пар сил, действующих на твёрдое тело необходимо и достаточно, чтобы модуль вектора момента эквивалентной пары сил равнялся нулю.

, отсюда: - 0

Необходимо и достаточно, чтобы алгебраическая сумма проекции векторов моментов пар сил на каждую из 3-х координатных осей была равна нулю.

Лекция 5.

Теорема о II переносе силы. (Метод Пуансо)

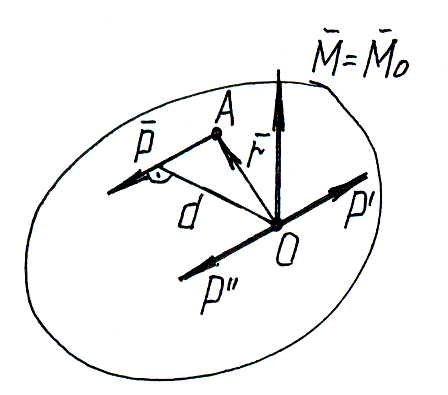
т.О центр приведения

в т.О 2 уравновешивающие силы и

,т. к. 0.

можно рассматривать как совокупность и пары .

Момент пары .

Совпадает не только модуль, но и направление момента силы относительно т.О и момента пары .

Момент пары как свободный вектор может быть приложен в любой точки плоскости приложим его в т.О.

Т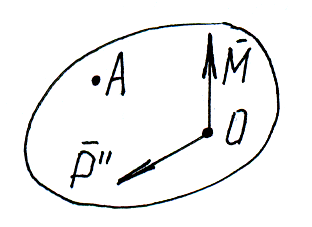 аким образом, силу , не изменяя её действия на твёрдое тело можно перенести из точки её приложения А в любой центр приведения О, приложив при этом к телу пару сил с моментом , геометрически равным моменту этой силы относительно центра приведения.

(Метод Пуансо (1777 -1850 г.г.)

Приведение произвольной системы сил к заданному центру; главный вектор, главный момент.

произвольно расположенные силы

т. приложения .

Приведём их к произвольному центру О.

Получим:

1). 3 силы приложены в т.О;

2). 3 приложенные пары

.

Складывая по правилу многоугольника, получим их равнодействующую , равную их геометрической сумме.

Геометрическая сумма всех сил системы называется главным вектором системы сил .

Складывая пары получим эквивалентную им пару. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения О.

Момент эквивалентной пары равен геометрической сумме моментов присоединенных пар.

Момент , равный геометрической сумме моментов сил данной системы относительно какой-либо точки, называется главным моментом системы сил относительно этой точки.

Распространяем полученные результаты на любое число сил:

Силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору, и приложенной в центре приведения, и к паре сил, с моментом, равным главному моменту всех сил относительно центра приведения.

Выбор центра приведения не отражается на , но влияет на модуль и направление главного момента.