Аналитическое выражение моментов силы относительно координатных осей.

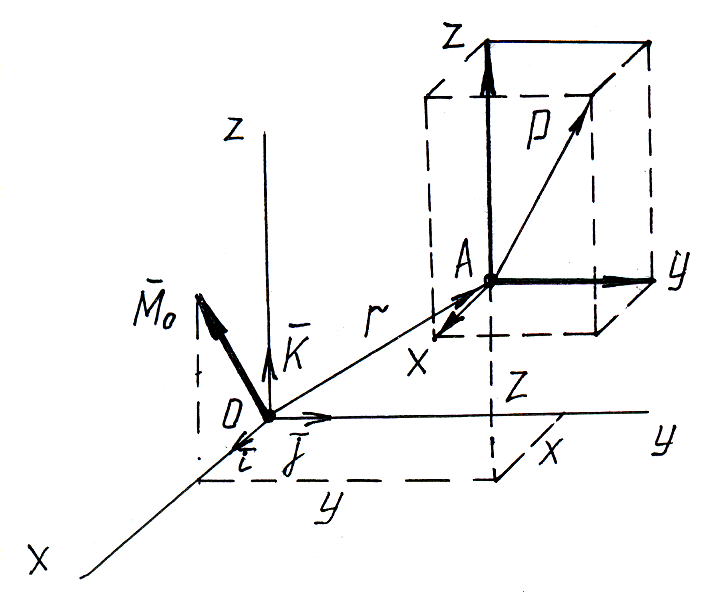
Разложим на составляющие по осям , где , , -проекции на координатные оси, равные моментам относительно координатных осей.

Из векторной алгебры известно:

можно записать:

-аналитическое выражение моментов силы относительно координатных осей.

Лекция 4.

Пара сил. Момент пары сил.

Система двух равных по модулю, параллельных и противоположно направленных сил и , называются парой сил.

П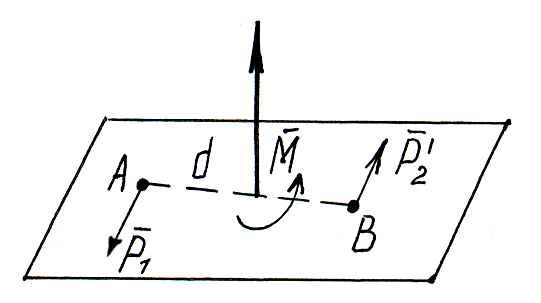 лоскость, в которой находятся линии действия и , называется плоскостью действия пары сил.

Пара сил не имеет равнодействующей (силы пары не уравновешиваются, т.к. не направлены по одной прямой). Пара сил стремится произвести вращение твердого тела. Пара сил не имея равнодействующей, не может быть уравновешена силой.

d-плечо пары – кратчайшее расстояние между линиями действия сил.

Действие пары сил на твердое тело характеризуется ее моментом.

Момент пары сил определяется произведением модуля одной из сил на ее плечо:

(Н/м)

момент пары изображается вектором.

Вектор момента пары , , направляют перпендикулярно к плоскости действия пары сил в такую сторону, чтобы, смотр навстречу этому вектору, видеть пару сил, стремящуюся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки.

Если рассматривают пары, лежащие только в одной плоскости, то ее совмещают с плоскостью чертежа. Вместо вектора момента пары перпендикулярной к плоскости чертежа указывают только направление, в котором пара будет вращать плоскость.

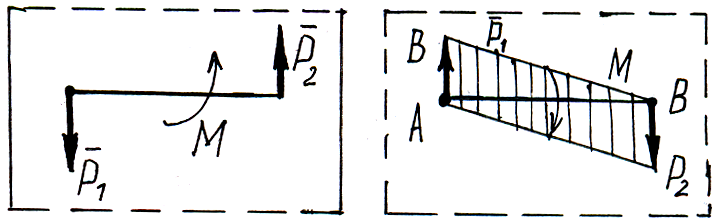
Тогда (момент пары рассматривается как алгебраическая величина)

«+», если против хода часовой стрелки

«­­­–», если по часовой стрелке.

Теоремы об эквивалентности пар сил.

1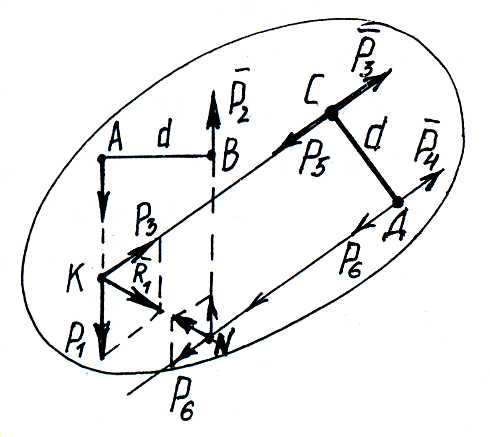 ) действие пары на твердое тело не изменится, если ее перенести в любое место в плоскости ее действия (пару можно поворачивать в плоскости ее действия на любой угол).

Пара сил с плечом d.

,

т .к. ,

П олучаем ,

т .к. 0

Суммы их направлены по диагонали ромба в противоположные стороны.

2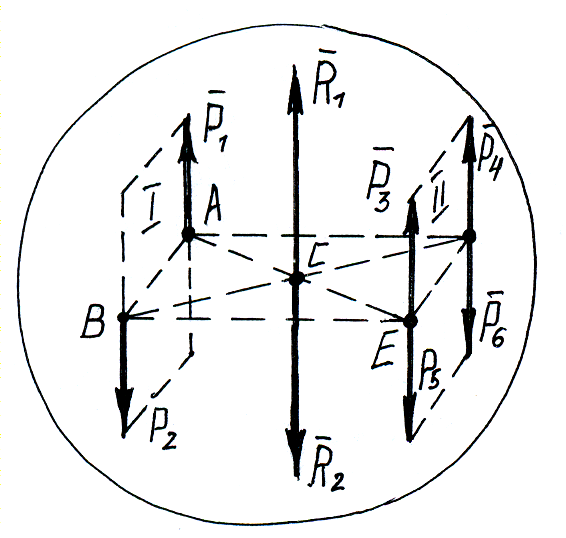 ) Действие пары на твердое тело не изменяется, если перенести плоскость действия пары параллельно самой же.

П ара лежит в плоскости I. Плоскость II параллельна плоскости I. АВ=DE. 0

ABDE – параллелограмм, диагонали которого в т.С делятся пополам.

уравновешиваются.

О стается пара , лежащая в плоскости II. Получаем

3 ) Действие пары на твердое тело не изменится, если изменить плечо и модули сил, сохраняя неизменным момент пары (пару можно поворачивать в плоскости ее действия на любой угол).

Разложим силу на (точка приложения т.С) и . В т.А получим силу Получим новую пару

Рассмотрим

, отсюда .

Получили момент пары моменту пары Заметим, что момент пары равен моменту одной из сил относительно точки другой.

Следствие из 3 теорем:

1). Момент пары можно переносить в любую точку. Момент пары - свободный вектор.

2). Если моменты пар , равны, то пары эквивалентны.