Аналитический способ сложения сходящейся системы сил

Для аналитического задания силы необходимо выбрать систему координационных осей, по отношению к которым будет определяться направление силы в пространстве.

Вектор, изображающий силу, можно построить, если известны её проекции на прямоугольные декартовы оси координат.

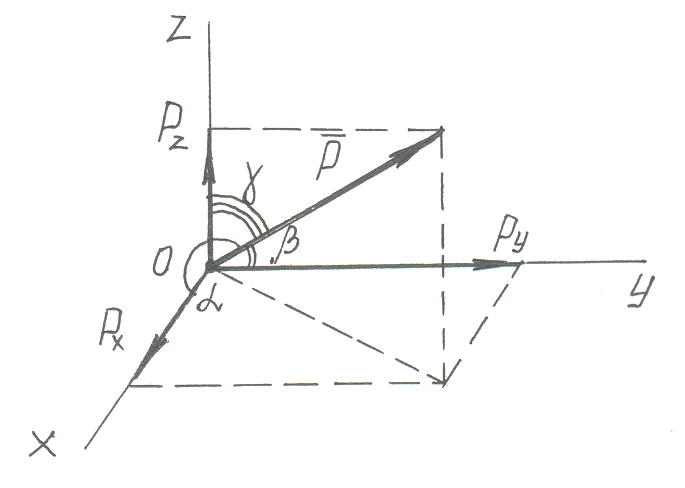
Сила разложена на составляющие , которые численно равны проекциям силы на соответствующие оси. Отсюда следует, что если известны проекции силы на оси координат, то можно вектор силы построить геометрически.

,

где

Чтобы сложить силы аналитически, необходимо вычислить проекции сил на координатные оси.

Аналитическое условие равновесия сходящейся системы сил.

, т.е. и , тогда

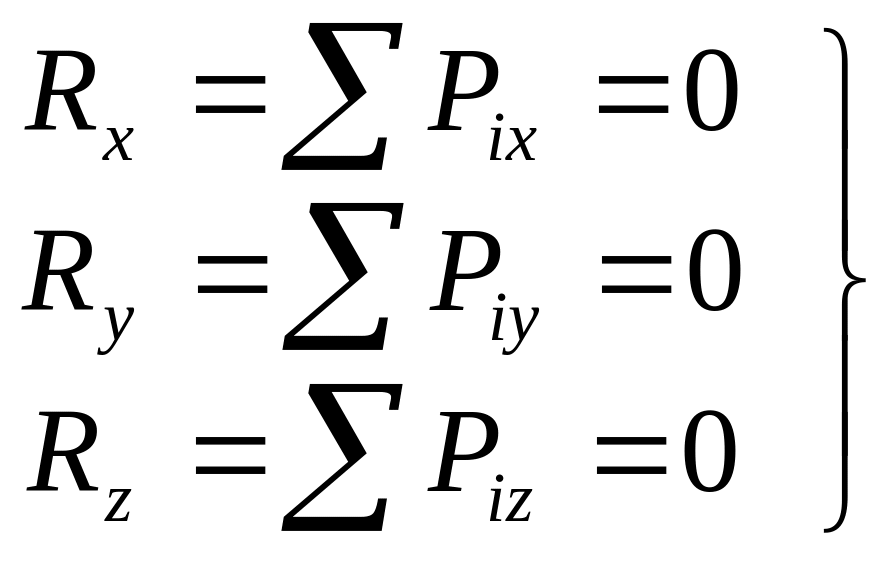
-аналитическое выражение равновесия пространственной сходящейся системы сил.

- для плоской системы сил

Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три взаимноперпендикулярных оси были равны 0.

Лекция 3.

М омент силы относительно точки.

Дано: тело с неподвижной т.О, в т.А приложена сила , которая стремится повернуть тело вокруг т.О. Такое действие силы называется вращательным эффектом. Вращательный эффект изменяется моментом силы относительно точки: .

Момент силы относительно т.О изображается вектором приложенным в этой точке и направленным перпендикулярно к плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу , стремящуюся вращать эту плоскость в сторону, обратную вращению часовой стрелки.

Модуль этого вектора: ,

где d – плечо - кратчайшее расстояние от т.О до линии действия силы.

Модуль можно выразить

Момент силы равен, нулю если d=0

Если в т.А провести , то

, но

Вектор момента силы относительно т.О можно рассматривать как векторное произведение , проведенного из этой точки в точку приложения силы на вектор силы .

Момент силы относительно оси.

П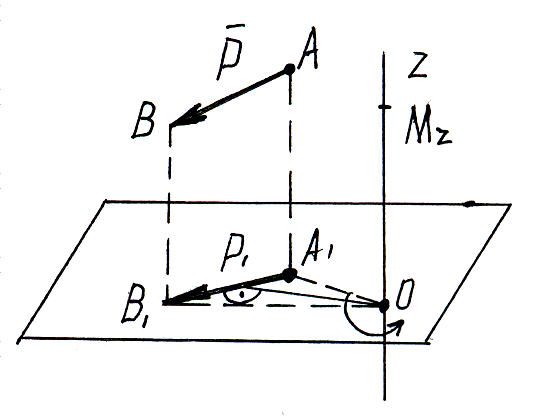 усть на твердое тело в т.А действует . Чтобы вычислить момент этой силы относительно оси Z, следует спроектировать на плоскость, перпендикулярную к оси Z, а затем вычислить момент ее проекции на эту плоскость относительно т.О пересечения оси с плоскостью, приписав этому моменту знак «+» или «­­­­­–».

Моментом силы относительно оси Z называется взятое со знаком «+» или «–» произведение модуля проекции силы на плоскость перпендикулярную оси, на ее плечо d₁ относительно т.О₁ пересечения оси с плоскостью.

Момент «+», если смотря навстречу оси Z, можно видеть стремящейся вращать плоскость вокруг оси z против часов стрелки.

Момент изображается отрезком, отложенным по оси Z от т.О., в положительном направлении, если >0 и в отрицательном, если <0.

момент силы относительно оси равен 0, если:

1)линия действия силы параллельна оси

2)линия действия силы пересекает ось

отсюда следует: если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен 0.

Зависимость между моментами силы относительно точки и оси, проходящей через эту точку.

Мы установили, что

,

т.к. является проекцией на плоскость, перпендикулярную оси Z, то , где -угол между плоскостями.

Известно, что угол между плоскостями равен углу между перпендикулярами, проведенными к этим плоскостям, т.е. углу между и осью Z.

Следовательно,

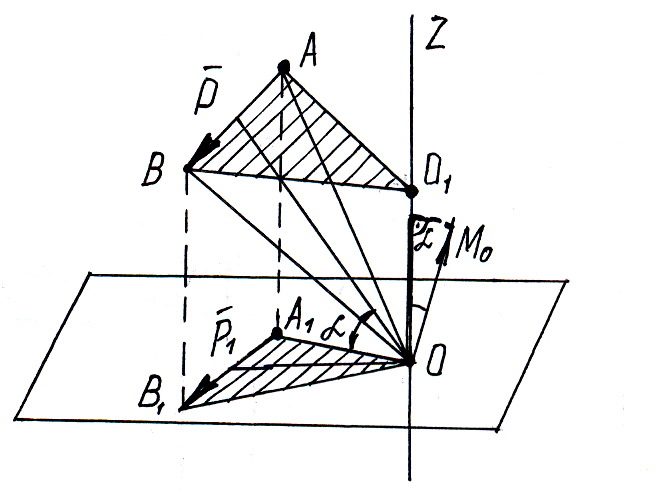
Проекция момента силы относительно точки на ось, проходящую через эту точку , равна моменту силы относительно этой оси. Если сила расположена в плоскости, перпендикулярной оси, то