
- •Аксиомы статики.
- •Несвободное тело. Связи. Реакция связей.
- •Принцип освобождаемости твердых тел от связей.
- •Система сходящихся сил.
- •Г еометрический способ сложения.
- •Геометрическое условие равновесия системы сходящихся сил.
- •Теорема о равновесии трех непараллельных сил.
- •Теорема о проекции равнодействующей системы сил.
- •Аналитический способ сложения сходящейся системы сил
- •Аналитическое условие равновесия сходящейся системы сил.
- •М омент силы относительно точки.
- •Момент силы относительно оси.
- •Зависимость между моментами силы относительно точки и оси, проходящей через эту точку.
- •Аналитическое выражение моментов силы относительно координатных осей.
- •Пара сил. Момент пары сил.
- •Теоремы об эквивалентности пар сил.
- •Сложение пар сил.
- •Условия равновесия пар сил.
- •Теорема о II переносе силы. (Метод Пуансо)
- •Приведение произвольной системы сил к заданному центру; главный вектор, главный момент.
- •Вычисление главного вектора и главного момента системы сил п роизвольно расположенных на плоскости.
- •Уравнения равновесия системы сил, произвольно расположенной в плоскости.
- •У равнения равновесия параллельных сил.
- •Главный вектор и главный момент произвольной пространственной системы сил.
- •Условие равновесия произвольной пространственной системы сил.
- •Равновесие пространственной параллельной системы сил.
- •Распределенные силы.
- •Теорема о моменте равнодействующей силы (теорема Вариньона).
- •Статически определенные и статически неопределенные задачи.
- •Равновесие системы соединенных тел.
- •Равновесие при наличии сил трения.
- •Законы трения скольжения.
- •Экспериментальное определение коэффициента трения.
- •Реакции шероховатых связей. Угол трения.
- •Равновесие при наличии трения.
- •Расчет ферм.
- •Приведение системы параллельных сил к равнодействующей.
- •Центр тяжести твердого тела-
- •Центр тяжести плоской фигуры. С татический момент площади плоской фигуры относительно оси.
- •Центр тяжести линии.
- •Определение центра тяжести плоской фигуры по центрам тяжести ее частей. Способ отрицательных площадей.
Лекция 1.
Теоретическая механика - это наука, в которой изучаются общие законы движения и взаимодействия материальных тел.
Механическим движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и во времени.
Механическим взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их механического движения.
Теоретическая механика состоит из трех разделов.
Статика изучает методы преобразования системы сил в эквивалентные системы и изучает условия равновесия сил, приложенных к твердому телу.
Кинематика изучает движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
Динамика изучает движение материальных тел в пространстве в зависимости от действующих на них сил.
Приступая к изучению механики, следует определить ее основные понятия.
Материальное тело - это тело, которое занимает какой-то объем в пространстве.
Материальная точка – это материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать. Материальная точка обладает массой и способностью взаимодействовать с другими телами.
Системой материальных точек или механической системой называется такая совокупность материальных точек, в которой положение и движение каждой материальной точки зависит от положения и движения других точек этой системы.
Абсолютно твердым телом называют такое материальное тело, геометрическая форма и размеры которого, не изменяются ни про каких механических воздействиях со стороны других тел.
Сила – это векторная физическая величина, которая характеризует механические взаимодействия материальных тел.
С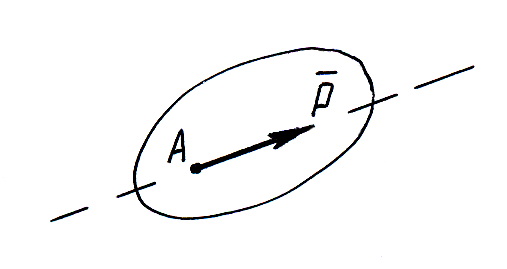
 ила
имеет модуль, направление и точку
приложения. Прямая по которой направлена
сила называется линией
действия силы.
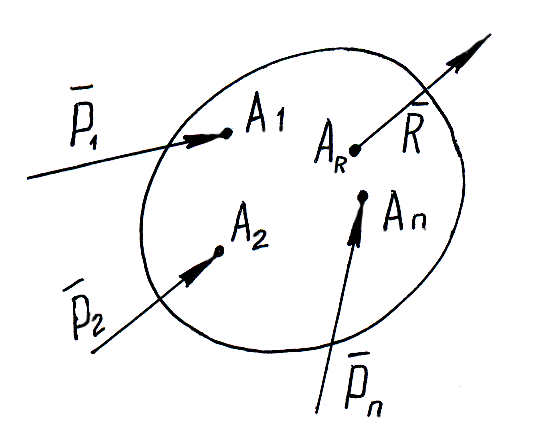
Совокупность нескольких называется
системой
сил. системы
сил, под действием каждой из которых
твердое тело находится в одинаковом
кинематическом состоянии, называется
эквивалентными
системами.
Сила, эквивалентная некоторой системе
называется равнодействующей.
ила
имеет модуль, направление и точку
приложения. Прямая по которой направлена
сила называется линией
действия силы.
Совокупность нескольких называется
системой
сил. системы
сил, под действием каждой из которых
твердое тело находится в одинаковом
кинематическом состоянии, называется
эквивалентными
системами.
Сила, эквивалентная некоторой системе
называется равнодействующей.
Д![]() ано:
материальное тело А, на которое действует
система сил
ано:
материальное тело А, на которое действует
система сил
![]()
![]()
Сила равная по модулю равнодействующей и направленная в противоположную сторону называется уравновешивающей силой.
С истема сил, которая будучи приложенной к твердому телу, находящемуся в покое не выводит его из состояния покоя, называется системой взаимноуравновешивающихся сил или системой 0.
Силы, действующие на механическую систему, делятся на внешние и внутренние.
Внешними называются силы, действующие на материальные точки данной системы со стороны материальных точек, не входящих в данную систему.
Внутренними называются силы взаимодействия между материальными точками рассматриваемой системы.
Аксиомы статики.
1) Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка движется равномерно прямолинейно или находится в состоянии покоя.
2) Аксиома равновесия двух сил. Две силы, приложенные к твердому телу взаимноуравновешиваются только в том случае, если их модули равны и они направлены в разные стороны по одной прямой.

![]()
![]() 0
0
3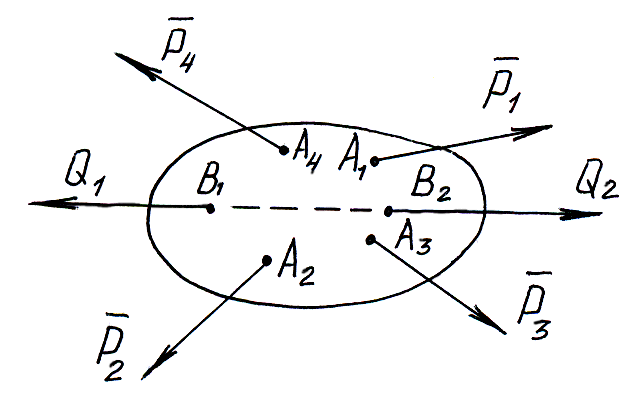 )
Аксиома
присоединения и исключения уравновешивающихся
сил. Действие
системы сил на твердое тело не изменится,
если к ней присоединить или из нее
исключить систему взаимно уравновешивающих
сил.
)
Аксиома
присоединения и исключения уравновешивающихся
сил. Действие
системы сил на твердое тело не изменится,
если к ней присоединить или из нее
исключить систему взаимно уравновешивающих
сил.
![]()
![]()
С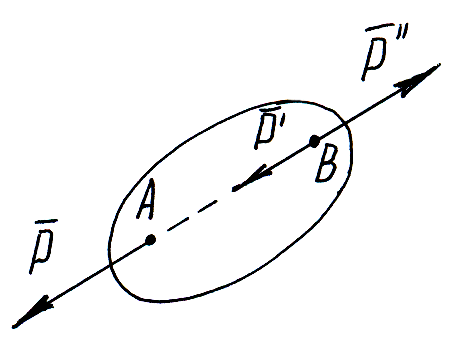 ледствие:
не изменяя кинематического состояния
твердого тела, силу можно переносить
вдоль линии ее действия, сохраняя ее
модуль и направление.
ледствие:
не изменяя кинематического состояния
твердого тела, силу можно переносить
вдоль линии ее действия, сохраняя ее
модуль и направление.
![]()
![]() и
и
![]() взаимноуравновешивающиеся тогда, в т.В
будет приложена к телу сила
взаимноуравновешивающиеся тогда, в т.В
будет приложена к телу сила
![]() .
Сила –
скользящий вектор.
.
Сила –
скользящий вектор.
4) Аксиома
параллелограмма сил.
Равнодействующая пересекающихся сил,
приложенная в точке их пересечения и
изображается диагональю параллелограмма,
построенного на этих силах:
![]() .
Модуль равнодействующей:
.
Модуль равнодействующей:
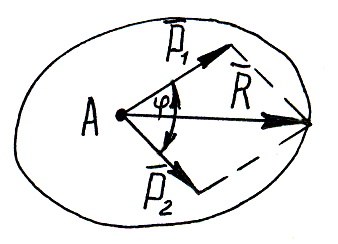
![]()
5) Аксиома действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.
![]()
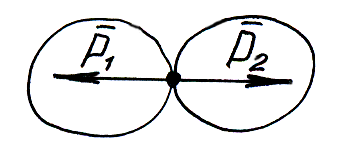
В природе не существует одностороннего действия сил. Будучи противоположными к разным телам эти силы не уравновешиваются.
6) Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу сохраняется при его затвердении. Из этой аксиомы следует, что условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, приложенных к деформируемому телу. Однако эти условия необходимы, но недостаточны.
Несвободное тело. Связи. Реакция связей.
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тела, ограничивающие свободу движения твердого тела, являются по отношению к нему связью.
Твердое тело, свобода движения которого ограничена связями, называется несвободным.
Все силы, действующие на несвободное тело, наряду с внешними и внутренними, можно также разделить на задаваемые или активные силы и реакции связей.
Задаваемые силы выражают действие на твердое тело других тел.
Реакцией связи называется сила или система сил, выражающая механическое действие на тело.
Принцип освобождаемости твердых тел от связей.
Н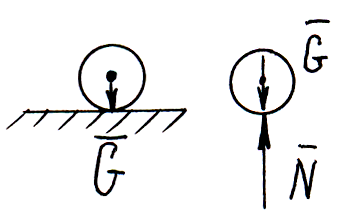
 есвободное
твердое тело можно рассматривать как
свободное, на которое, кроме задаваемых
сил, действуют реакции связей.
есвободное
твердое тело можно рассматривать как
свободное, на которое, кроме задаваемых
сил, действуют реакции связей.
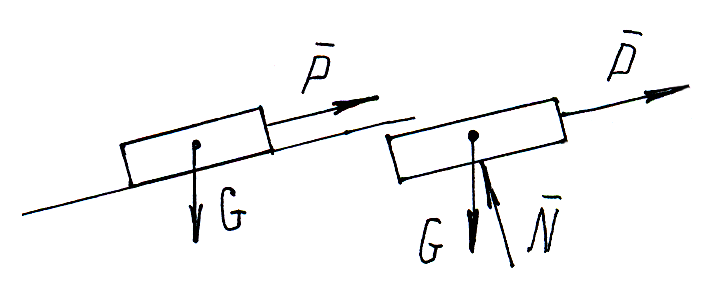
Реакция гладкой плоскости направлена перпендикулярно к плоскости.
Р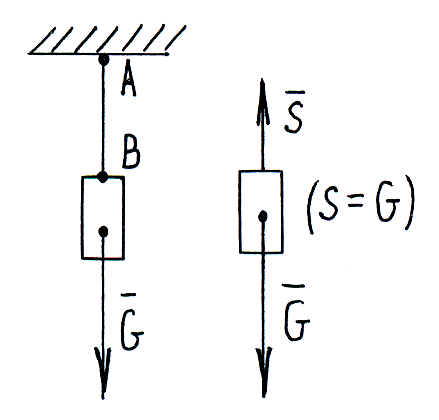
 еакция
нити направлена вдоль нити.
еакция
нити направлена вдоль нити.
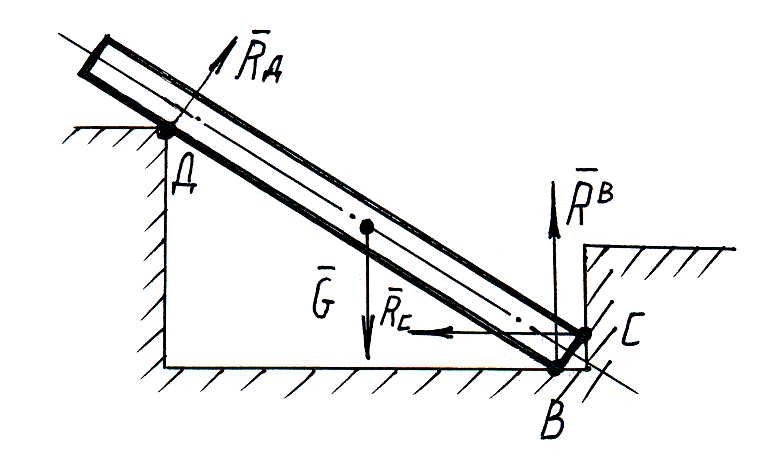
т. D – точечная опора.
Если одна из соприкасающихся поверхностей является точкой, то реакция направлена по нормали к другой поверхности.
Если (известно) существует два взаимноперпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление реакций противоположно первому направлению.
Стержневая опора.
Б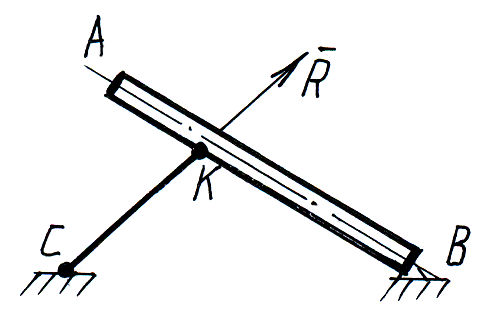 алка
АВ поддерживается стержнем КС. Реакция
стержня направлена по стержню.
алка
АВ поддерживается стержнем КС. Реакция
стержня направлена по стержню.
Шарнирные опоры:
а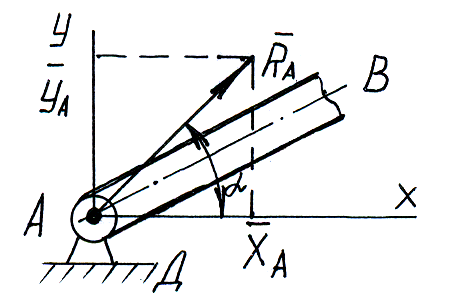 )
Неподвижный
шарнир
(цилиндрический)
)
Неподвижный
шарнир
(цилиндрический)
Е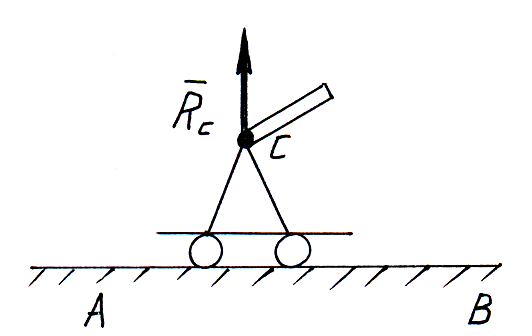 сли
два тела соединены болтом, проходящим
через отверстия в этих телах, то такое
соединение называется шарнирным. Реакция
цилиндрического шарнира может иметь
любое направление в плоскости,
перпендикулярной к оси шарнира.
сли
два тела соединены болтом, проходящим
через отверстия в этих телах, то такое
соединение называется шарнирным. Реакция
цилиндрического шарнира может иметь
любое направление в плоскости,
перпендикулярной к оси шарнира.
б) Подвижный шарнир
в) Шаровой (сферический) шарнир и подпятник.
Э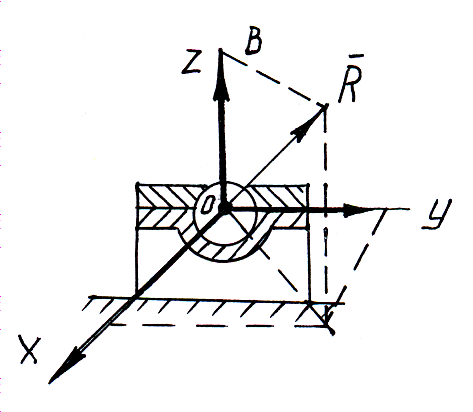
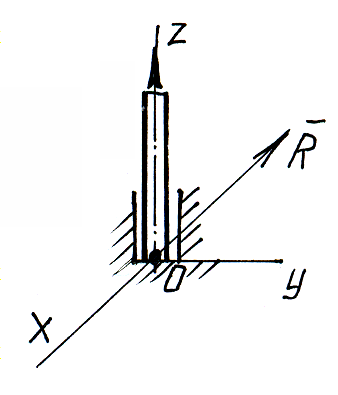 та
связь закрепляет какую-нибудь точку
твердого тела так, что она не может
совершать никаких перемещений в
пространстве. Реакция
шарового шарнира и подпятника может
иметь любое направление в пространстве.
та
связь закрепляет какую-нибудь точку
твердого тела так, что она не может
совершать никаких перемещений в
пространстве. Реакция
шарового шарнира и подпятника может
иметь любое направление в пространстве.
Лекция 2.
