Передач с эвольвентным профилем зубьев

Межосевое расстояние при (см. рис. 31) или .

Приняв суммарное число зубьев найдем .

В прямозубой передаче ширина венца равна длине зуба: , где — коэффициент длины зуба (ширины венца) по модулю (для цилин­дрических прямозубых передач); выбирается по табл. 2.

Таблица 4. Значение коэффициента

, не более	HB	Характеристика конструкции
45-30 30-20	До 350 Свыше 350	Высоконагруженные точные передачи. Валы, опоры и корпуса повышенной жесткости
30-25 20-15 15-10	До 350 Свыше 350	Обычные передачи редукторного типа в отдельном кор­пусе с достаточно жесткими валами и опорами. Передачи низкой точности с консольными валами

Таблица 5. Геометрические параметры прямозубой цилиндрической передачи

Параметр, обозначение	Расчетные формулы
Модуль т
Диаметр вершин зубьев da
Делительный диаметр d
Диаметр впадин зубьев df
Высота зуба h
Высота головки зуба ha
Высота ножки зуба hf
Окружная толщина зуба
Окружная толщина впадин зубьев
Радиальный зазор с
Межосевое расстояние
Окружной шаг рt
Длина зуба (ширина венца)

Определение числа зубьев шестерни и колеса по суммарному числу зубьев передачи и известному передаточному числу. Если известно и , то число зубьев шестерни и колеса можно определить по формулам:

; ,

где — число зубьев шестерни; — число зубьев колеса; — суммарное число зубьев; и — передаточное число.

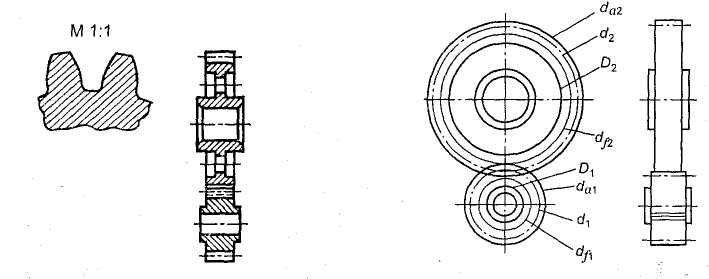
Рис. 32 Рис. 33

Расчет зубьев цилиндрической прямозубой передачи на изгиб

По международному стандарту ISO / DIS 6336: (Ausgabe 1986) по расчету зубчатых передач предусмотрены четыре метода расчета зубчатых передач.

Метод А – экспериментально – исследовательский требует точных измерений, обширного и трудоёмкого математического анализа или обоснования на основе надежного эксплуатационного эксперимента на подобных приводах. При этом предел выносливости и эквивалентное окружное усилие или коэффициент внешней динамики – К_А определяется из полученного измерением коллектива нагрузок с использованием гипотез накопления повреждений. Поскольку величина К_А может принять весьма большие значения от 1 до 2 и более, то применяемый метод расчета и величина К_А должны согласовываться между изготовителем и покупателем редуктора. Как видим, метод очень дорог и применяется крайне редко.

Метод В - экспериментально- теоретический и производится на основе исследования предела выносливости зубчатого колеса – представителя, считается целесообразным для зубчатых передач массового производства.

Метод С - приближенный, при этом аналитический расчет производится на основе комплексных данных стандарта или справочной технической литературы.

Метод D – упрощенный, примерно соответствует приводимому расчету данного раздела.

Необходимо заметить, что метод расчета зубчатых передач по ГОСТу 21354-87 занимает промежуточное положение между методами С и D. В методе С коэффициент формы зуба при расчете на изгиб рассматривается как произведение двух переменных

Ниже излагается упрощенный метод расчета зуба на изгиб, осно­ванный на положениях сопротивления материалов.

На рис. 34 показаны схема зацепления двух зубьев в полюсе и силы, действующие на зубья колес со стороны шестерни; трение не учитывается. Нормальная сила F_n раскладывается на две составляющие: окружную силу F_t и радиальную или распорную — F_r.

Рис. 34. Усилия в зацеплении прямозубой цилиндрической передачи

При выводе формул принимают следующие упрощения и допущения: зуб рассматривают как консольную балку прямоугольного сечения, работаю­щую на изгиб и сжатие; вся нагрузка, действующая в зацеплении, переда­ется одной парой зубьев и приложена к их вершинам; нагрузка равномерно распределена по длине зуба .

На рис.35 показан профиль балки равного сопротивления (s — тол­щина зуба в опасном сечении; l — плечо изгибающей силы; — длина зуба; F_n — нормальная сила, действующая на зуб).

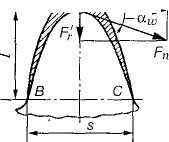
Рис.35. Схема расчета зубьев на изгиб

Определим силы в опасном сечении корня зуба. Разложим силу F_n в точке А на две составляющие: F_t' и F'_r, условно принимаем, что сила F_n приложена только к одному зубу (перекрытием пренебрегаем), а сила F_t равна окружной силе на начальной окружности.

Сила F_t' изгибает зуб, а сила F'_r сжимает его. Из рис. 35 находим

;

где — угол направления нормальной силы F_n, приложенной у вершины, который несколько больше угла зацепления ; — нормаль­ная сила.

Исходя из изложенного выше, за расчетное напряжение принима­ют напряжения на растянутой стороне зуба:

(1)

Для опасного сечения ВС условие прочности

(2)

где — напряжение изгиба в опасном сечении корня зуба; W — осевой момент сопротивления; — площадь сечения ножки зуба.

Выразим I и s в долях модуля зубьев: l= km; s = cm, где к и с — коэффи­циенты, зависящие от формы зуба, т.е. от угла и числа зубьев Z.

Тогда изгибающий момент в опасном сечении

осевой момент сопротивления прямоугольного сечения зуба

(3)

Подставим в формулу (2) входящие в него параметры М_И и W, введем коэффициенты расчетной нагрузки (табл. 6), (табл. 7) и теоре­тический коэффициент концентрации напряжений К_Т.

В результате получим окончательную формулу проверочного расчета прямозубой передачи на усталость при изгибе

(4)

где Y_F — коэффициент учитывающий форму зуба и концентрацию напря­жений (табл. 8).

Таблица 6. Значение коэффициентов и

Расположение шестерни отно­сительно опор	Твердость НВ поверхностей зубьев колеса	при						при
		0,2	0,4	0,6	0,8	1,2	1,6	0,2	0,4	0,6	0,8	1,2	1,6
Консольное (опоры — шари­коподшипники)	До 350 Св. 350	1,16 1,33	1,37 1,70	1,64				1,08 1,22	1,17 1,44	1,28
Консольное (опоры — роли­коподшипники)	До 350 Св. 350	1,10 1,20	1,22 1,44	1,38 1,71	1,57			1,06 1,11	1,12 1,25	1,19 1,45	1,27	-
Симметричное	До 350 Св. 350	1,01 1,02	1,03 1,04	1,05 1,08	1,07 1,14	1,14 1,30	1,26	1,01 1,01	1,02 1,02	1,03 1,04	1,04 1,07	1,07 1,16	1,10 1,26
Несимметричное	До 350 Св. 350	1,05 1,09	1,10 1,18	1,17 1,30	1,25 1,43	1,42 1,73	1,61	1,03 1,06	1,05 1,12	1,07 1,20	1,12 1,29	1,19 1,48	1,28 -

Таблица 7. Значение коэффициентов и

Степень точности передачи	Твердость НВ поверхности зубьев колеса	при окружной скорости, м/с
		1	2	3	6	8	10
7	До 350 Св. 350	1,08/1,03 (1,04/1,02) 1,03/1,01 (1,03/1,00)	1,16/1,06 (1,07/1,03) 1,05/1,02 (1,05/1,01)	1,33/1,11 (1,14/1,05) 1,09/1,03 (1,09/1,02)	1,50/1,16 (1,21/1,06) 1,13/1,05 (1,14/1,03)	1,62/1,22 (1,29/1,07) 1,17/1,07 (1,19/1,03)	1,80/1,27 (1,36/1,08) 1,22/1,08 (1,24/1,04)
8	До 350 Св. 350	1,10/1,03 (1,04/1,01) 1,04/1,01 (1,03/1,01)	1,20/1,06 (1,08/1,02) 1,06/1,02 (1,06/1,01)	1,38/1,11 (1,61/1,04) 1,12/1,03 (1,10/1,02)	1,58/1,17 (1,24/1,06) 1,16/1,05 (1,16/1,03)	1,78/1,23 (1,32/1,07) 1,21/1,05 (1,22/1,04)	1,96/1,29 (1,40/1,08) 1,26/1,08 (1,26/1,05)
9	До 350 Св. 350	1,13/1,04 (1,05/1,01) 1,04/1,01 (1,04/1,01)	1,28/1,07 (1,10/1,03) 1,07/1,02 (1,07/1,01)	1,50/1,14 (1,20/1,05) 1,14/1,04 (1,13/1,02)	1,72/1,21 (1,30/1,07) 1,21/1,06 (1,20/1,03)	1,98/1,28 (1,40/1,09) 1,27/1,08 (1,26/1,04)	2,25/1,35 (1,50/1,12) 1,34/1,09 (1,32/1,05)

Примечание. В числителе — значения для прямозубых колес, в знаменателе — для косозубых.

Таблица 8. Коэффициент -для эвольвентного наружного зацепления при a_w = 20° (при х = О)

Число зубьев		Число зубьев		Число зубьев
17	4,26	28	3,81	65	3,62
20	4,07	30	3,79	80	3,60
22	3,98	35	3,75	100	3,60
24	3,92	40	3,70	150	3,60
26	3,88	45	3,66	300	3,60
		50	3,65	Рейка	3,63

Примечание. Выбор коэффициента можно производить по графику.

Выведем формулу проверочного расчета прямозубых передач на уста­лость при изгибе через вращающий момент Т₂..

С учетом того, что ; формула проверочного расчета (4) примет вид

(5)

где , , МПа; m, мм; T₂ — вращающий момент на колесе, Нмм; Z₁ — число зубьев шестерни; — коэффициент длины зуба (ширины венца) по делительному диа­метру (табл. 9).

Таблица 9. Рекомендуемые значения коэффициента

в зависимости от твердости рабочих поверхностей зубьев

Расположение колес относи­тельно опор	или
Симметричное	0,8-1,4	0,4-0,9
Несимметричное	0,6-1,2	0,3-0,6
Консольное	0,3-0,4	0,2-0,25

Из формул (5) и (6) получаем формулы проектировочного рас­чета на изгиб

(6)

(7)

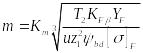(8)

где K_m = 1,4 для прямозубых колес.

В формулу (8) подставляют меньшее из двух отношений , вы­численных для шестерни и колеса.

Выбор допускаемых напряжений изгиба. Выше отмечалось, что при­чиной поломки зубьев, как правило, является усталость материала под дейст­вием повторных переменных изгибающих напряжений. Поэтому значения допускаемых напряжений должны быть определены исходя из предела вы­носливости зубьев. Допускаемое напряжение изгиба определяют по формуле

, (9)

где — базовый предел выносливости зубьев при отнулевом цикле изменения напряжений (табл. 10); S_F — коэффициент безопасности (S_F = 1,7 ÷ 2,2; S_F> 2,2 — для литых заготовок); Y_R — коэффициент, учиты­вающий шероховатость поверхности зуба (Y_R= 1,05 ÷ 1,2 — при полирова­нии, в остальных случаях Y_R= 1); K_FC — коэффициент, учитывающий влия­ние двустороннего приложения нагрузки (K_FC= 1,0 — при одностороннем приложении нагрузки, изгибающей зуб; K_FC= 0,65 — для нормализованных сталей, K_FC=0,75 — для закаленных сталей с твердостью свыше HRC45; K_FC = 0,9 — для азотированных сталей); K_FL — коэффициент долговечности.

Таблица 10. Приближенные значения пределов выносливости при изгибе зубьев

, МПа	Твердость зубьев HRС		Сталь	Способ термиче­ской или хими­ко-термической обработки
	Поверх­ность	Сердцеви­на
1,8HBСР	НВ 180-300		Углероди­стая или лег тированная	Отжиг, нормализа­ция или улучшение
550-600	HRC 45-55		Легирован­ная	Объемная закалка
750-850	48-58	30-45		Поверхностная за­калка
750-850	56-62	32-45		Цементация и нит-роцементация
300 + 1,2HRC (сердцевины зуба)	50-60	24-40		Азотирование

В зависимости от твердости активных поверхностей зубьев коэф­фициент долговечности Y_N определяется по следующим формулам:

K_FL = при НВ≤ 350, (10)

K_FL = при НВ ≥ 350, (11)

где — число циклов соответствующее точке перелома кривой усталости; N_F — расчетная циклическая долговечность;

, (12)

где — частота вращения (угловая скорость) шестерни или колеса, об/мин (рад/с); с — число колес, находящихся в зацеплении с рассчиты­ваемым колесом; — продолжительность работы зубчатой передачи за рас­четный срок службы, ч;

, (13)

где L_Г — срок службы передачи, год; С — число смен; t_c — продолжитель­ность смены, ч; k_Г — коэффициент годового использования привода; k_с — коэффициент использования привода в смене.

Формула (12) приемлема для определения расчетной циклической долговечности только при постоянном режиме нагрузки.

При выборе материала для зубчатой пары с целью сокращения номенк­латуры, как правило, назначают одинаковые материалы. Разность значений твердостей для шестерни и колеса достигается их термической обработкой. Получение нужных механических характеристик зависит не только от тем­пературного режима обработки, но и от размеров заготовки.

При переменном режиме нагрузки расчетная циклическая долговеч­ность определяется по формуле:

, (14)

где K_FE — коэффициент приведения переменного режима нагрузки к по­стоянному эквивалентному режиму:

(15)

где T_max, Т_i — максимальные и промежуточные значения моментов; коэф­фициент m_F = 6 — при нормализации и улучшении; m_F=9 — при закалке; t_i — продолжительность (в часах) действия момента Т_i; — суммарная про­должительность работы зубчатой передачи.

Расчет цилиндрической прямозубой передачи на контактную прочность

Расчет прочности контактирующих поверхностей зубьев основан на ограничении наибольших нормальных напряжений.

При выводе формул приняты следующие допущения: зубья рассматри­вают как два находящихся в контакте цилиндра с параллельными образую­щими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно рас­пределенной по длине зуба; контактирующие профили предполагают не­разделенными масляной пленкой.

На основании этих допущений к расчету зубчатых колес можно приме­нить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:

(16)

где — расчетная удельная нормальная нагрузка; — приведенный мо­дуль упругости материалов зубьев; — приведенный радиус кривизны профилей зубьев шестерни и колеса; — коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки

, (17)

где — нормальная сила, действующая на зуб (см. рис. 35); — окружная сила; — суммарная длина контактной линии (для прямозубых передач — ширина венца, так как ; здесь — коэффициент, учитывающий непостоянство суммарной длины контактной линии); — коэффициент перекрытия.

Для учета неравномерности распределения нагрузки по длине контакт­ных линий, а также для учета динамических нагрузок вследствие погреш­ности изготовления и деформации деталей передачи вводят коэффициент нагрузки (см. табл. 6-7).

Отсюда

(18)

Приведенный модуль упругости , где и — мо­дули упругости материалов шестерни и колеса.

Зубья рассматриваются как цилиндры длиной (ширина зубчатого ко­леса) и радиусов и , где

Приведенный радиус кривизны зубьев в полюсе

Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внут­реннего зацепления.

Подставляя значения и в формулу (17), после преобразований получим

(19)

Обозначим в формуле (19) выражение через — коэффи­циент, учитывающий форму сопряженных поверхностей зубьев;

— коэффициент, учитывающий механические свойства

материалов сопряженных колес ( = 275 МПа^1/2 — для стальных колес);

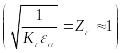— коэффициент, учитывающий суммарную длину контактных линии для прямозубых передач.

Получим расчетную формулу, рекомендуемую для проверочного расчета:

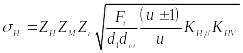(20)

После подстановки значений ; и в формулу (20) и некоторых преобразований получим удобную для расчета формулу

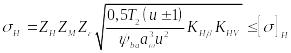(21)

Значение определяют по формуле ( — см. табл. 9).

После некоторых преобразований формулы (21) получим формулу проектировочного расчета для определения межосевого расстояния прямозу­бых зубчатых передач:

Обозначим через вспомогательный коэффициент

(для прямозубых передач при = 1,25, = 49,5 МПа^1/3).

Тогда формула проектного расчета для определения межосевого рас­стояния закрытых цилиндрических передач

(22)

Допускаемые контактные напряжения (МПа) при расчете рабочих поверхностей на усталостное выкрашивание рассчитываются по формуле

,

где — предел выносливости рабочих поверхностей зубьев (табл. 11), соответствующий базовому числу циклов перемены напряжений , МПа (база испытаний определяется по табл. 12);

— коэффициент безопасности ( = 1,1 при нормализации, улучше­нии или объемной закалке; при поверхностной закалке и цементации =1,2);

— коэффициент, учитывающий шероховатость сопряженных по­верхностей зубьев ( );

— коэффициент долговечности, который учитывает влияние срока службы, режима нагрузки передачи и возможность повышения допускае­мых напряжений для кратковременно работающих передач.

Таблица 11. Пределы контактной выносливости

, МПа	Материал	Твердость поверхностей зубьев (средняя)	Термическая обработка зубьев
2 НВ + 70 18 HRC+150 17 HRC +200	Сталь углеродистая и легированная	НВ < 350 HRC 38-50 HRC 40-50	Нормализация, улучшение Объемная закалка Поверхностная закалка
23HRC 1050	Сталь легированная	HRC> 56 HV 550-750	Цементация и нитроцементация Азотирование

Таблица 12. Базовое число циклов

Твердость поверх­ностей зубьев НВ	До 200	250	300	350	400	450	500	550	600
, млн. циклов	10	17,0	26,4	38,3	52,7	70	90	113	140

При постоянной нагрузке ; (или ) — циклическая долговечность.

При переменной нагрузке расчетная циклическая долговечность опре­деляется по формуле:

,

где К_НЕ — коэффициент приведения переменного режима нагружения к постоянному эквивалентному

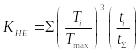
В расчетные формулы (21) и (22) входит меньшее из допускаемых напряжений, установленных для шестерни и колеса. Так как материал ко­леса имеет обычно меньшую твердость, чем материал шестерни, то в боль­шинстве случаев для колеса меньше.

В табл. 11 даны значения предела выносливости (база испыта­ний) для различных материалов зубчатых колес.

Последовательность проектировочного расчета цилиндрической прямозубой передачи

Исходными данными для расчета передачи обычно являются мощность (или вращающий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Расчет закрытой цилиндрической прямозубой передачи.

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев (табл. 13).

Таблица 13. Предпочтительные марки сталей для изготовления зубчатых колес

Термическая обработка	Твердость НВ (HRC)	d, мм
		Любой	315	200	125	80
		b, мм
		Любая	200	125	80	50
Нормализация, улучшение	179-207 235-262 269-302	45	45 35ХМ	45 40Х 35ХМ	45 45 40Х	45 45 45
Поверхностная закалка ТВЧ	(45-50) (50-56)	—	—	35ХМ 50ХМ	35ХМ 50ХМ	35ХМ 50ХМ
Цементация Нитроцементация Азотирование	(56-63) (56-63) (50-56)	—	—	20ХН2М 25ХГТ 40ХН2МА	20ХН2М 25ХГТ 40ХН2МА	20ХН2М 25ХГТ 40ХН2МА

3. Определить базу испытаний N_HO, расчетную циклическую долговеч­ность N_H, вычислить коэффициенты и допускаемые напряжения изгиба.

4. Выбрать коэффициент длины зуба (ширины венца колеса) и рассчи­тать .

5. Определить межосевое расстояние из условия контактной прочности по формуле (22) и округлить его значение до стандартного.

Для стандартных редукторов расчетное значение а_ш округляют до бли­жайшего большего значения: 40, 50, 63, 80, 100, 125, (140), 160, (180), 200, (225), 250, (280), 315, (335), 400, (450), 500, (560), 630, (710), 800, (900), 1000 и т. д. до 25 000 (в скобках значения по 2-му ряду стандарта для ).

6. Задать модуль из соотношения и округлить его значение до ближайшего стандартного (см. табл. 3). При этом в силовых передачах желательно, чтобы модуль был не менее 1,5—2 мм.

7. Определить суммарное число зубьев , передачи, числа зубьев шес­терни и колеса.

8. По табл. 8 выбрать коэффициенты формы зубьев Y_Fi и Y_F2 для шес­терни и колеса.

9. Проверить прочность зубьев по напряжениям изгиба. При неудовле­творительных результатах ( или ) необходимо путем соот­ветствующего изменения числа зубьев и модуля; при том же межосевом расстоянии добиться уменьшения напряжений изгиба, не нарушая пр; этом условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 5).

11. Определить окружную скорость колеса v и по табл. 14 назначить соответствующую степень точности зацепления.

Таблица 14. Значения окружной скорости колес

Вид передачи	Форма зубьев	Твердость поверх­ностей зубьев коле­са (большего) НВ	Окружная скорость v (м/с, не бо­лее) при степени точности
			6	7	8	9
Цилиндрическая	Прямые Не прямые	До 350 Св. 350 До 350 Св. 350	18 15 36 30	12 10 25 20	6 5 12 9	4 3 8 6
Коническая	Прямые	До 350 Св. 350	10 9	7 6	4 3	3 2,5

Примечание. Во избежание получения чрезмерно высоких значений коэффициентов нагрузки рекомендуется степень точности назначать на единицу выше, чем указано в таблице.

Расчет открытых передач. Иногда открытые передачи рассчитывают так же, как закрытые. Рекомендуется следующая последовательность расчета.

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы колес, назначить их термическую обработку и значения твердости рабочих поверхностей зубьев.

3. Определить расчетную долговечность, вычислить коэффициенты режима работы и определить допускаемые напряжения изгиба.

4. Задать число зубьев шестерни и по передаточному числу опг: делить число зубьев колеса z₂.

5. Определить по табл. 8 коэффициенты формы зуба Y_F.

6. Выбрать коэффициент длины зуба (ширины венца колеса ).

7. Из условия прочности на изгиб определить модуль передачи т и округлить его до ближайшего большего стандартного значения (см. табл. 3)

8. Произвести геометрический расчет передачи (см. табл. 5).

9. Определить окружную скорость колес и по табл. 14 соответствующую ее степень точности зацепления.

Цилиндрические косозубые и шевронные зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 36). У косозубых колес оси зубьев располагаются не по образующей делитель­ного цилиндра, а по винтовой линии, составляющей с образующей угол (рис. 37). Угол наклона зубьев р принимают равным , он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.

Рис. 36. Цилиндрическая косозубая передача

Передаточное число для одной пары колес может быть . В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диа­гонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до пря­мой, «диагонально» захватывающей зуб, и постепен­но уменьшается до точки).

Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные дина­мические нагрузки.

За счет наклона зуба в зацеплении косозубой передачи появляется осевая сила.

Направление осевой силы зависит от на­правления вращения колеса (рис. 37), на­правления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагру­жает валы и опоры, что является недостатком косозубых передач.

Рис. 37. Усилия в косозубой цилиндрической передаче

Шевронные зубчатые колеса пред­ставляют собой разновидность косозубых колес (рис. 38).

а) б)

Рис. 38. Шевронная зубчатая передача

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 38, а), называют шеврон­ным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шев­ронные колеса с жестким углом (рис. 38, б), предназначенным для выхо­да режущего инструмента при нарезании зубьев. Шевронные передачи об­ладают всеми преимуществами косозубых, а осевые силы (рис. 39) проти­воположно направлены и на подшипник не передаются.

Рис.39. Усилия в зацеплении шевронных зубчатых колес

В этих передачах допускают большой угол наклона зубьев ( ). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т.е. в тех случаях, когда требует­ся передавать большую мощность и высокую скорость, а осевые нагрузки нежелательны.

Рис. 40

Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 44) по делительной окружности — нормальный шаг р_п, в торцовой плоскости — торцовый шаг р_t. Из условия, что модуль зацепления равен шагу, деленному на число , имеем ; .

Для косозубых и шевронных колес значения нормального модуля т_n стандартизованы, так как профиль косого зуба в нормальном сечении со­ответствует исходному контуру инструментальной рейки и, следовательно, т = т_п (косозубые и шевронные колеса нарезают, тем же способом и инст­рументом, что и прямозубые). Нормальный модуль т_п является исходным при геометрических расчетах.

Определим зависимость между нормальным и торцовым шагом и модулем через угол наклона зубьев.

Если левую и правую части разделим на , получим

; .

Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приве­денным в табл. 15. По торцовому модулю т_t рассчитывают делительные (начальные) диаметры, а до т_п — все остальные размеры зубчатых колес.

Таблица 15. Геометрические параметры цилиндрической косозубой передачи

Параметр, обозначение	Расчетные формулы
Нормальный модуль
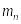
Торцовый (окружной модуль)
Диаметр вершин зубьев в
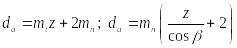
Делительный диаметр d
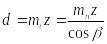
Диаметр впадин зубьев
Шаг нормальный
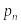
Шаг торцовый (окружной)
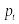
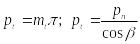
Окружная толщина зубьев
Ширина впадин зубьев
Высота зуба
Высота головки зуба
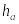
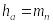
Высота ножки зуба
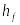
Радиальный зазор
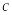
Межосевое расстояние
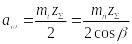
Длина зуба
Ширина венца

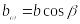
Окружная сила . На косой зуб действует осевая сила (см. рис. 37), радиальная (распорная) сила .

В косозубдй передаче сила , действующая на зуб косозубого колеса (см. рис. 44), направлена по нормали к профилю зуба, т.е. по линии зацепле­ния эквивалентного прямозубого колеса, и составляет угол с касательной к эллипсу.

Эту силу разложим на две составляющие: окружную силу на эквива­лентном колесе и радиальную (распорную) силу на этом колесе .

Если, в свою очередь, силу разложить по двум направлениям, то по­лучим такие силы: — окружную силу, — осевую.

Для зубчатого колеса с шевронным зубом окружную силу и рас­порную определяют по тем же формулам, что и для косозубой передачи т.е. , . В шевронной передаче осевая сила (см. рис. 39).

Винтовая передача (разновидность ко­созубой) состоит из двух косозубых цилиндри­ческих колес (рис. 41). Однако в отличие от косозубых цилиндрических передач с парал­лельными валами касания между зубьями здесь происходит в точке и при значительных скоро­стях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.

Рис.41. Винтовая зубчатая передача

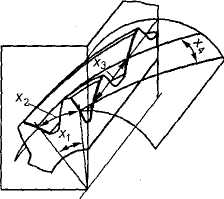
Рис. 42

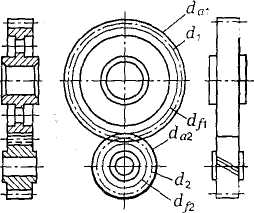
Рис. 43

Расчет зубьев цилиндрической косозубой и шевронной передач на изгиб

Расчет на изгиб косых и шевронных зубьев аналогичен расчету прямых зубьев.

Так как в косозубой и шевронной передачах зубья значительно прочнее прямых зубьев, то соответственно в расчетные формулы (5), (9) вводят коэффициенты, учитывающие повышение прочности при изгибе по срав­нению с прямыми зубьями.

Коэффициент формы зуба выбирают по табл. 8 в зависимости от эквивалентного числа зубьев приведенного колеса (см. рис. 44):

,

где — число зубьев приведенного (эквивалентного) колеса в сечении Б—Б (рис. 44); — фактическое число зубьев; — угол наклона зубьев.

Рис. 44. К расчету косозубых колес

Определение параметров приведенного цилиндрического колеса

Если зубчатое колесо рассечь нормальной плоскостью (см. рис.44), то в сечении начального цилиндра получим эллипс с полуосями и . Профиль зуба в этом сечении близок к профилю та­кого прямого зуба модуля , который расположится на цилиндрическом колесе радиусом , равным радиусу кривизны эллипса. Это колесо называется эквивалентным (приведенным) колесом. Радиус кривизны эл­липса . Диаметр эквивалентного колеса . Если в последнее выражение подставить , то полу­чится число зубьев эквивалентного колеса (эквивалентное или фиктивное число зубьев):

или

Проверочный расчет.

По аналогии с формулой (5) условие прочности зубьев на изгиб ци­линдрической косозубой передачи отличается введением поправочных ко­эффициентов:

- учитывающего перекрытие зубьев ;

- учитывающего угол наклона зуба (при среднее зна­чение );

- учитывающего распределение нагрузки между зубьями (выбирается по табл.16).

Таблица 16. Значение коэффициента ,

Степень точно­сти передачи	при окружной скорости , м/с
	5	10	15
6	1,01	1,03	1,04	0,72
7	1,05	1,07	1,09	0,81
8	1,09	1,13	—	0,91

Приняв , формула проверочного расчета косозубых передач на изгиб имеет вид

(23)

где — вращающий момент на колесе, Нмм; — передаточное число; — коэффициент длины зуба (табл. 9); — коэффициент формы зуба (табл. 8 выбирается по эквивалентному числу зубьев шестер­ни ); — число зубьев; — нормальный модуль, мм; и — коэффи­циенты расчетной нагрузки (см. табл. 6 и 7); — допускаемое напря­жение при изгибе, МПа (выбирается).

Расчет косозубых передач на изгиб ведется по менее прочному зубу у которого отношение меньшее.

Проектировочный расчет.

С учетом формулы (8) из формулы (23)

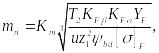(24)

где — нормальный модуль, мм; — вращающий момент, Нмм; — допускаемое напряжение при изгибе, МПа; — вспомогательный коэф­фициент (для косозубых передач учитывает также и ).

Расчет цилиндрической косозубой и шевронной передач на контактную прочность

Расчет на контактную прочность косозубых и шевронных колес производят аналогично расчету прямозубых колес, он является основным. Рас­положение зубьев в косозубом зацеплении повышает коэффициент пере­крытия зубьев, так как в зацеплении находится одновременно несколько пар зубьев, что уменьшает нагрузку на один зуб и повышает его контакт­ную прочность, увеличивает прочность зубьев на изгиб, уменьшает дина­мические нагрузки. Для учета повышения контактной прочности косых зубьев по сравнению с прямыми в формулу (21) вводят поправочные коэффициенты.

Контактные напряжения, возникающие в поверхностном слое косых зубьев:

(25)

где — коэффициент, учитывающий форму сопряжения по­верхностей зубьев (среднее значение ); =275 МПа — коэффи­циент, учитывающий механические свойства материала сопряженных ко­лес; — коэффициент, учитывающий суммарную длину кон­тактных линий (для косозубых передач среднее значение ); — коэффициент, учитывающий распределение нагрузки между зубьями (вы­бирается по табл. 16); (табл. 6), (табл.7) — коэффициенты ре­жима работы; — коэффициент длины зуба ( — табл. 9); — межосевое расстояние, мм; — передаточное отноше­ние; — момент на колесе, Нмм; — допускаемое контактное напря­жение, МПа.

Проектировочный расчет на контактную прочность.

Аналогично расчету прямозубой передачи получим фор­мулу проектировочного расчета для определения межосевого расстояния косозубой передачи:

(26)

где — вспомогательный коэффициент ( = 43 МПа^1/3 с учетом ).

Допускаемые нормальные контактные напряжения для расчета ци­линдрической косозубой передачи определяют как и для рассмотренных прямозубых передач. Часто материалы для шестерни и коле­са выбирают одинаковыми. Разные допускаемые контактные напряжения для шестерни и колеса обеспечиваются путем их различной термической обработки. Предпочтительные марки сталей даны в табл. 13.

В качестве допускаемого контактного напряжения (расчетного) для косозубых и шевронных цилиндрических передач принимают значение немного меньше среднего арифметического между значениями и , т.е.

(27)

где — допускаемое (расчетное) контактное напряжение; — допус­каемое контактное напряжение для материала шестерни; — допускае­мое контактное напряжение для материала колеса.

Расчетное не может быть принято большим, чем .

Последовательность проектировочного расчета цилиндрической косозубой передачи

Последовательность приведенного расчета аналогична расчету цилинд­рической прямозубой передачи.

Последовательность расчета закрытой цилиндрической косозубой передачи.

1. Определить передаточное число .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и твердость рабочих поверхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую долговечность, определить допускаемые напряжения изгиба и контактные напряжения.

4. Выбрать коэффициент длины зуба (ширины венца колеса).

5. Определить межосевое расстояние из условия контактной прочности по формуле (26).

6. Задать значение нормального модуля из соотношения и округлить его до ближайшего стандартного значения (см. табл. 3). При этом для силовых передач желательно иметь модуль не ме­нее 1,5—2 мм.

7. Задать угол наклона зубьев и определить суммарное число зубьев , передачи, числа зубьев шестерни и колеса и .

8. Определить эквивалентные числа зубьев и и коэффициенты фор­мы зуба и .

9. По формуле (23) проверить прочность зубьев по напряжениям из­гиба. При неудовлетворительных результатах ( или ) необ­ходимо путем соответствующего изменения числа зубьев и модуля при том же межосевом расстоянии добиться определенного изменения напряжения изгиба, не нарушая условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 15). Опре­делить окружную скорость колес и по табл. 14 назначить соответствую­щую степень точности, выбрать (табл. 16).

Расчет открытых передач (часто открытые передачи рассчитыва­ют так же, как закрытые).

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы для колес, назначить их термическую обработку и твердость рабочих поверхно­стей зубьев.

3. Определить базу испытаний базового числа циклов , расчетную циклическую нагрузку, вычислить коэффициенты и определить допускае­мые напряжения изгиба.

4. Задать угол наклона зубьев и число зубьев шестерни

5. Определить число зубьев колеса

6. Определить числа зубьев эквивалентных колес, шестерни и колеса и по табл.6 коэффициенты формы зуба и .

7. Выбрать — коэффициент длины зуба (ширины венца).

8. Из условия прочности на изгиб определить по формуле (24) значе­ние нормального модуля и округлить до ближайшего большего стан­дартного значения (см. табл. 3).

9. Произвести геометрический расчет передачи (см. табл. 15).

10. Определить окружную скорость колес и по табл. 14 назначить соответствующую ей степень точности.

Конические зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 45) и служит для передачи вращающего момента между валами с пересекающимися осями под углом . Наиболее распространена в машиностроении коническая передача с углом между осями Z=90⁰ (рис. 47), но могут быть передачи и с . Колеса конических передач. выполняют с прямыми (рис. 46, а), косыми (рис. 46, б), круговыми зубьями (рис. 46, в).

Рис. 45. Коническая пря­мозубая передача

Рис. 46. Конические зубчатые колеса: а — коле­со с прямыми зубьями;

б — колесо с косыми зу­бьями; в — колесо с круговыми зубьями

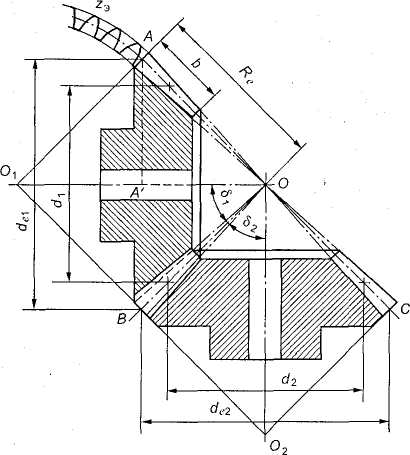
Рис. 47. Геометрические параметры конических зубчатых колес

Рис. 48. Гипоиднаяя передача

Передачу с коническими колесами для передачи вращающего момента между валами со скрещиваю­щимися осями называют гипоидной (рис. 48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже ци­линдрических при равных силовых параметрах. Их применение диктуется только необходимостью пе­редавать момент при пересекающихся осях валов. Передаточное число одной пары .

Вершины начальных и делительных конусов конической передачи на­ходятся в точке пересечения осей валов О (рис. 50). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи (рис. 47 и 50):

АОВ — делительный конус шестерни;

ВОС — делительный конус колеса;

АО₁В — делительный дополнительный конус шестерни;

ВО₂С — делительный дополнительный конус колеса;

— угол делительного конуса шестерни;

— угол делительного конуса колеса;

d_e[ — внешний делительный диаметр шестерни;

d_e2 — то же, колеса;

d₁ — средний делительный диаметр шестерни;

d₂ — то же, колеса;

b — ширина зубчатого венца (длина зуба);

R_e — внешнее делительное конусное расстояние (или длина дис­танции).

Рис. 50. Коническая прямозубая передача

Передаточное число конической передачи определяется так:

В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные окружности (см. рис. 47).

Из условия, что в конической передаче модуль и делительный связаны теми же соотношениями, что и в цилиндрических передачах, т.е. d=mz (рис.51), определяют внешний d_e и средний d_m делительные метры:

где т_е — внешний окружной модуль; т_т — средний окружной модуль.

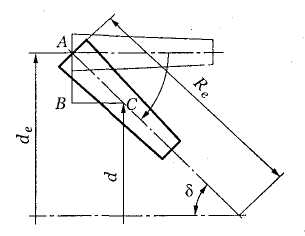
Рис. 51. Зуб конического колеса

Внешний окружной модуль обычно выбирают из стандартного ряда (см. табл. 3). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубча­тых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения).

Средний окружной модуль т рассчитывают в зависимости от внешнего окружного модуля т_е. По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Рис. 52

Зависимость между т_е и т_т в конической передаче.

Из рис. 3.51 , где (из ). Отсюда .

Умножив левую и правую части равенства на два, получим . Разделив левую и правую части равенства на , получим

или

Геометрические соотношения размеров прямозубой конической пере­дачи с эвольвентным профилем зуба. Согласно рис. 53 внешний диаметр вершин зубьев

внешний диаметр впадин зубьев

Длина зуба (ширина венца) [ при условии и , где — средний делительный диаметр шес­терни].

Рис. 53. Геометрия прямозубой конической передачи

Ориентировочно длина зуба может быть выбрана также в зависимости от внешнего делительного конусного расстояния R_e:

.

Таблица 17. Геометрические параметры прямозубой конической передачи

Параметр, обозначение	Расчетные формулы
Внешний окружной модуль
Средний окружной модуль
Внешний диаметр вершин зубьев
Внешний делительный диаметр
Внешний диаметр впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Окружной шаг
Окружная толщина зуба
Окружная ширина впадины
Радиальный зазор
Ширина зубчатого венца
Внешнее делительное конусное расстояние
Угол делительного конуса шестерни
колеса

Силы в зацеплении прямозубой конической передачи. В рассматривае­мой передаче действует одна сила, обусловленная давлением зуба шестерни на зуб колеса. Эта сила для удобства расчетов раскладывается на 3 состав­ляющие: окружная F_t, радиальная F_r и осевая F_a.

С учетом геометрических соотношений в конической передаче по нор­мали к зубу действует сила F_n1 (рис. 54). Эту силу разложим на две состав­ляющие: и . В свою очередь разложим на и . Запишем:

; ; .

Осевая сила на шестерне численно равна радиальной силе на колесе.

Рис. 54. Силы в зацеплении прямозубой конической передачи

Рис.55

Рис. 56

Расчет зубьев прямозубой конической передачи на изгиб

Расчет производят по аналогии с расчетом цилиндрической прямозу­бой передачи.

Опытным путем установлено, что нагрузочная способность конической передачи ниже, чем цилиндрической. В соответствии с этим в расчетные фор­мулы для зубьев конической передачи вводят коэффициент К_FO, учитываю­щий снижение их нагрузочной способности по сравнению с зубьями ци­линдрических передач.

Расчет на прочность зубьев при изгибе производят по среднему значе­нию модуля зубьев т. Коэффициент формы зуба Y_F выбирают по аналогии с цилиндрической прямозубой передачей, но в зависимости от числа зубь­ев эквивалентных колес .

Под числом зубьев эквивалентных колес понимают такое число зубь­ев, которое может расположиться на длине окружности (см. рис. 47) ра­диусом, равным длине образующей дополнительного конуса О₁А.

Проверочный расчет следует проводить по аналогии с прямозубой пе­редачей.

Расчетные напряжения изгиба в зубьях конических колес и условие прочности выражаются формулой

(28)

где — возникающее напряжение изгиба, МПа; — вращающий момент на колесе, Нмм; , — коэффициенты нагрузки (см. табл. 6, 7); — коэффициент длины зуба; — коэффициент формы зуба (выбирают по табл. 8) в зависимости от ; — число зубьев шестер­ни; и — передаточное число; — средний модуль, мм; = 0,85 — опытный коэффициент снижения нагрузочной способности; — допускаемое напряжение изгиба, МПа.

Проектировочный расчет. Средний модуль зубьев определяется по формуле

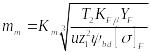(29)

где т, мм; Т₂, Нмм; , МПа; К_т= 1,45 — вспомогательный коэффици­ент для стальных прямозубых конических колес; принимают .

Расчет конических прямозубых передач на контактную прочность

В основу данного расчета берется формула (20) в параметрах эк­вивалентной цилиндрической прямозубой передачи по среднему дополнительно­му конусу

Используем связь тригонометрических функций для определе­ния передаточного числа и делительного диаметра эквива­лентного колеса .

После подстановки в исходную формулу значений и и несложных преобразований получим формулу проверочного расчета для стальных пря­мозубых конических колес

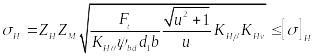(30)

или, заменив ; , получим:

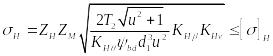
Па^1/2 (для стальных колес), (31)

где — возникающее нормальное контактное напряжение, МПа; — средний делительный диаметр шестерни, мм; — вращающий момент на колесе, Нмм; — коэффициент, учитывающий форму сопряжения по­верхности зубьев; — коэффициент, учитывающий механические свойст­ва материала; — коэффициент ширины (длины) зуба; — передаточное число; = 0,85 — коэффициент, учитывающий снижение контактной прочности конической передачи по сравнению с прямозубой; — допускаемое контактное напряжение. Из двух значе­ний выбирается меньшее.

Проектировочный расчет.

Решая уравнение (31) относительно запишем

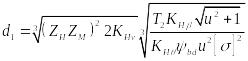
(32)

где — вспомогательный коэффициент (для стальных прямозубых конических колес K_d =78 МПа^1/3).

Последовательность проектировочного расчета конической зубчатой передачи

Последовательность расчета закрытой передачи.

1. Определить передаточное число и углы делительных конусов шес­терни и колеса и .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую дол­говечность , коэффициенты режима, допускаемые контактные напряже­ния и допускаемые напряжения изгиба.

4. Выбрать коэффициент длины зуба.

5. Определить средний делительный диаметр из условия контактной прочности [формула (32)].

6. Задать число зубьев шестерни , определить число зубьев колеса

7. Рассчитать внешний модуль , и округлить его до стандартного зна­чения (см. табл. 3), а также средний модуль .

8. Определить числа зубьев эквивалентных колес и и по табл. 8 — коэффициенты формы зуба шестерни и колеса .

9. Проверить прочность зубьев по напряжениям изгиба. При неудовле­творительных результатах необходимо путем соответствующего изменения числа зубьев и модуля при том же конусном расстоянии до­биться определенного изменения напряжений изгиба, не нарушая при этом условия контактной прочности.

10. Произвести геометрический расчет передачи (см. табл. 17).

11. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности.

Последовательность расчета открытых конических передач.

1. Определить передаточное число и углы делительных конусов шестерни и колеса и .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и значения твердости рабочих по­верхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую дол­говечность, коэффициенты режима и определить допускаемые напряжения изгиба.

4. Задать число зубьев шестерни и по передаточному числу опреде­лить число зубьев колеса .

5. Определить число зубьев эквивалентных колес и коэффициен­ты формы зуба и по табл. 8.

6. Выбрать коэффициент длины зуба (ширины венца) .

7. Из условия прочности на изгиб (формула 29) определить средний модуль , после чего подсчитать внешний модуль , значение которого округлить до ближайшего большего стандартного (см. табл. 3). При необ­ходимости следует пересчитать в зависимости от стандартного .

8. Произвести геометрический расчет передачи (см. табл. 17).

9. Определить окружную скорость колес и по табл. 14 назначить со­ответствующую степень точности зацепления.

Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения

Основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты.

Решая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л.Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.

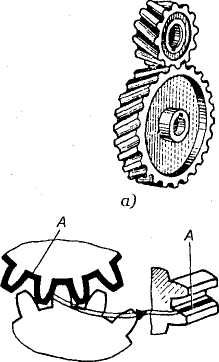
Передачи с зацеплением Новикова состоят из двух цилиндрических косозубых колес (рис. 57, а) или конических колес (рис. 57, б) с винто­выми зубьями и служат для передачи момента между валами с параллель­ными или пересекающимися осями. Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт (рис. 57, в) заменен точечным, превращающимся под нагрузкой в контакт с хорошим прилеганием (рис.57, г). Простейшими профилями зубьев, обес­печивающими такой контакт, являются профили, очерченные по дуге окруж­ности или близкой к ней кривой.

б)

в)

Рис. 57. Передача с зацеплением М. Л. Новикова. А - площадка контакта

Обычно профиль зубьев шестерни делается выпуклым, а профиль зубь­ев колес вогнутым или наоборот (рис.58, а, б), но могут быть передачи и с профилем зубьев шестерни и колеса, показанным на рис.58, в. Выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4-1,8 раза большие вращающие моменты.

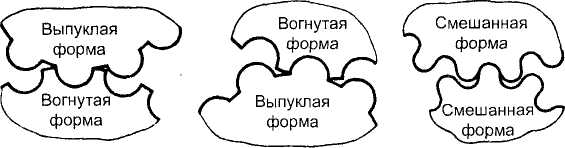
a) б) в)

Рис. 58. Профили зубьев в передачах с зацеплением М. Л. Новикова

В зацеп­лении Новикова контакт зубьев теоретически осуществляется в точке, в эвольвентном зацеплении соприкосновение зубьев происходит по линии. Однако при одинаковых габаритных размерах передачи соприкосновение зубьев в зацеплении Новикова значительно лучше, чем соприкосновение в эвольвентном зацеплении.

К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных машин это не так важно.

Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления.

В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев ( ) и дают достаточную жёсткость шестерён при их большой относительной ширине.

Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями.

Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п.

Достоинства и недостатки передач с зацеплением Новикова. Высо­кая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше до­пускаемой нагрузки для эвольвентных прямозубых передач тех же основ­ных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффици­енте нагрузки К= 1).

Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны, имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой пе­редаваемой мощности.

Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между со­прикасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи.

Потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении. Шум во время их работы значи­тельно ниже.

Недостатками являются:

- большая (чем в эвольвентных зацеплениях) чувствительность к изме­нению межосевого расстояния;

- с увеличением нагрузки в зацеплении возрастает осевая составляю­щая, что, в свою очередь, усложняет конструкцию применяемых подшипниковых узлов;

- при ухудшении контакта (например, в случае перекоса валов и изме­нения межосевого расстояния) вся нагрузка, действующая на зубья, может сосредоточиться на небольшом участке длины зубьев, в ре­зультате чего зубья могут оказаться сильно перегруженными;

- необходимость иметь две специальные фрезы для нарезания зубьев (для шестерни и колеса).

Стандартные исходные контуры для цилиндрической зубчатой пере­дачи с зацеплением Новикова для выпуклых (шестерня) и вогнутых (колесо) зубьев (рис. 59, а).

Основные геометрические размеры этих передач (рис. 59, б) опреде­ляют в зависимости от значения нормального модуля т_п (табл. 18 и 19).

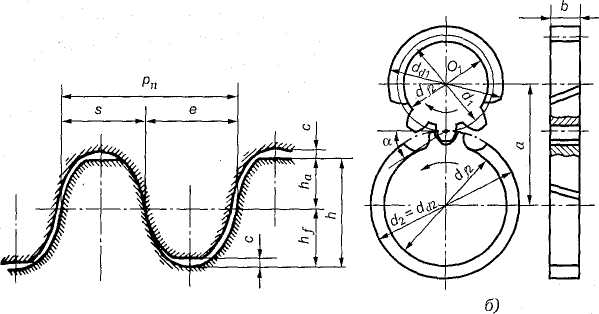
а)

Рис. 59. Косозубая передача с зацеплением М.Л. Новикова

Таблица 18. Стандартные значения модулей для передачи с зацеплением Новикова

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд
1,6		6,3		25
2,0	1,8	8	7,1		28
2,5	2,25	10	9	31,5	35,5
3,15	2,8	12,5	П,2	40	45
4	3,55	16	14	50	56
5	4,5	20	18	63
	5,6		22,4

Таблица 19. Геометрические параметры передачи с зацеплением Новикова

Параметр, обозначение	Расчетные формулы
Нормальный модуль
Торцовый модуль
Диаметр вершин зубьев
Делительный диаметр
Основной диаметр
Диаметр впадин зубьев
Нормальный шаг
Торцовый шаг
Осевой шаг
Окружная толщина зубьев
Окружная ширина впадин зубьев
Высота зуба
Высота головки зуба
Высота головки зуба
Радиальный зазор с
Ширина венца b
Межосевое расстояние

Примечание. — угол наклона зубьев; ; — целое число осевых шагов р_х в ширине венца; — часть ширины венца больше целого числа осевых шагов (ширину венца рекомендуется выбирать с учетом выполнения условия ); — суммарное число зубьев.

Расчет передачи с зацеплением Новикова на контактную прочность

Этот расчет производят по аналогичным расчетным формулам на контактную прочность для косых зубьев эвольвентного зацепления, но с учетом их большей нагрузочной способности. На основании опытных данных несущую способность зубьев зацепления Новикова по контактной прочности принимают в 1,75-2 раза больше, чем для эвольвентных зацеплений.

Условия контакта в передачах с зацеплением Новикова отличаются от условий контакта по Герцу (малая разность r₁ и r₂ большие значения и ). Учитывается экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев.

Контактные напряжения приближаются к напряжениям смятия. Рас­чет передач Новикова по контактным напряжениям применяют условно и ведут аналогично расчету с эвольвентным зацеплением.

Для зацепления Новикова коэффициент К_а = 33,6 МПа^1/3, а при расчете эвольвентной передачи К_а = 49,5...43 МПа^1/3. Это объясняется тем, что не­сущая способность зубьев с зацеплением Новикова в 1,75-2 раза больше по сравнению с эвольвентными передачами.

Ширина колеса не влияет на прочность зубьев на излом при зацепле­нии Новикова. В передачах с зацеплением Новикова нагрузка, распреде­ленная на площадке контакта, приложена не по всей длине зуба, как это имеет место в эвольвентном зацеплении, а лишь на сравнительно неболь­шом его участке. При этом значительная часть зуба практически ее не вос­принимает. Следовательно, изменение ширины венца колеса b при неиз­менном угле наклона зуба в отличие от эвольвентных колес практически не сказывается на прочности зубьев на излом.

Планетарные зубчатые передачи. Устройство передачи и расчет на прочность

Передачи, имеющие зубчатые или фрикционные колеса с перемещающимися осям, называют планетарными. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Наиболее распространена зубчатая однорядная планетарная передача (рис.60). Она состоит из центрального колеса 1 с наружными зубьями, неподвижного (центрального) колеса 2 с внутренними зубьями и водила на котором закреплены оси планетарных колес g (или сателлитов).

Рис.60. Планетарная передача

Водило вместе с сателлитами вращается вокруг центральной оси, а са­теллиты обкатываются по центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет. При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.

Планетарную передачу, совершаемую подвижными звеньями (оба иентральных колеса и водило), называют дифференциалом. С помощью диффе­ренциала одно движение можно разложить на два или два движения сло­жить в одно: от колеса 2 движение можно передавать одновременно колесу 1 и водилу h или от колес 1 и 2 к водилу g и т. д. Планетарную передачу ус­пешно применяют в транспортном машиностроении, станкостроении, приборостроении.

Достоинства и недостатки планетарных передач.

Основное достоинство — широкие кинематические возможности, по­зволяющие использовать передачу в качестве редуктора коробки скоро­стей, передаточное число в которой изменяется путем поочередного тормо­жения различных звеньев, и как дифференциальный механизм.

- Планетарный принцип позволяет получать большие передаточные чис­ла (до тысячи и больше) без применения многоступенчатых передач.

- Эти передачи компактные и имеют малую массу. Переход от простых передач к планетарным позволяет во многих случаях снизить их массу в 4 раза и более.

- Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.

- Эти передачи работают с меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и регулирование скорости;

- Имеют малый шум вследствие замыкания сил в механизме.

Основные недостатки: повышенные требования к точности изготовле­ния и монтажа (для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом); резкое снижение КПД передачи с увеличением передаточ­ного отношения.

Передаточное отношение.

Для определения передаточного отношения планетарной передачи ис­пользуется метод Виллиса — метод останова водила.

Передаточное отношение планетарной передачи (см. рис. 60)

(33)

где и — угловые скорости колес 1 и 2 относительно води­ла h; и — числа зубьев этих колес.

Для реальной планетарной передачи (колесо 2 закреплено неподвиж­но, колесо 1 — ведущее, водило h ведомое) при из формулы (36) получим

или

(34)

Для однорядной планетарной передачи , для многоступен­чатых , для кинематических передач . Чем больше передаточное отношение планетарной передачи, тем меньше КПД (0,99...0,1).

Расчет на контактную прочность зубьев планетарных передач проводится по аналогии с расчетом обыкновенных зубчатых передач от­дельно для каждого зацепления (см. рис.60): пара колес 1—g (внешнее зацепление) и g—2 — (внутреннее). Для таких передач достаточно рассчи­тать только внешнее зацепление, так как модули и силы в зацеплениях одинаковые, а внутреннее зацепление прочнее внешнего.

Проектировочный расчет планетарной передачи на контактную ус­талость активных поверхностей зубьев проводится по следующей формуле:

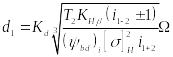(35)

где d₁ — делительный диаметр ведущего звена (шестерни), мм; K_d = 78 МПа — вспомогательный коэффициент (рассматриваются сталь­ные прямозубые колеса); T₂ — вращающий момент на шестерне, Нмм; — коэффициент нагрузки (см. табл.4); — коэффици­ент, учитывающий неравномерность распределения нагрузки среди сател­литов; — передаточное отношение; — коэффициент длины зуба (ширины колеса); — допускаемое контактное напряжение, МПа.

При расчете планетарных передач выбор числа зубьев колес зависит не только от передаточного отношения , но и от условий собираемости пере­дач. При этом сумма зубьев центральных колес должна быть кратной числу сателлитов (лучше 3).

Волновые зубчатые передачи. Устройство передачи и расчет на прочность

Волновые передачи основаны на принципе передачи вращательного движения за счет бегущей волновой деформации одного из зубчатых колес.

Такая передача была запатентована американским инженером Массером в 1959 г.

Волновые передачи имеют меньшие массу и габариты, большую кинематическую точность, меньший мёртвый ход, высокую вибропрочность за счёт демпфирования (рассеяния энергии) колебаний, создают меньший шум.

При необходимости такие передачи позволяют передавать движение в герметичное пространство без применения уплотняющих сальников, что особенно ценно для авиационной, космической и подводной техники, а также для машин химической промышленности.

Кинематически эти передачи представляют собой разновидность плане­тарной передачи с одним гибким зубчатым колесом. На рис. 61 изображе­ны основные элементы волновой передачи: неподвижное колесо 7 с внут­ренними зубьями, вращающееся упругое колесо 2 с наружными зубьями и водило h. Неподвижное колесо закрепляется в корпусе и выполняется в виде обычного зубчатого колеса с внутренним зацеплением. Гибкое зубча­тое колесо имеет форму стакана с легко деформирующейся тонкой стенкой: в утолщенной части (левой) нарезаются зубья, правая часть имеет форму вала. Водило состоит из овального кулачка и специального подшипника.

Рис. 61. Волновая передача

Гибкое колесо деформируется так, что по оси овала I—I зубья зацепля­ются на полную рабочую высоту; по оси II—II зубья не зацепляются.

Передача движения осуществляется за счет деформирования зубчатого венца гибкого колеса. При вращении водила волна деформации бежит по окружности гибкого зубчатого венца; при этом венец обкатывается по не­подвижному жесткому колесу в обратном направлении, вращая стакан и вал. Поэтому передача и называется волновой, а водило — волновым генератором.

При вращении водила овальной формы образуются две волны. Такую передачу называют двухволновой. Бывают трехволновые передачи, на рис. 62 показана схема такой передачи.

Рис. 62. Трехволновая передача

Достоинство и недостатки волновых передач.

Волновые передачи обладают большой нагрузочной способностью (в за­цеплении находится большое число пар — зубьев) и высоким передаточным числом (< 300 для одной ступени) при сравнительно малых габаритах. Это основные достоинства этих передач. Передача может работать, находясь в герметизированном корпусе, что очень важно для использования волновых передач в химической, авиационной и других отраслях техники.

Недостатки волновой передачи: практически индивидуальное, дорогостоящее, весьма трудоемкое изготовление гибкого колеса и волнового генератора; возможность использования этих передач только при сравнительно невысокой угловой скорости вала генератора; ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн; мелкие модули зубьев 1,5-2 мм)

Передаточное отношение волновых передач определяется методом остановки водила (метод Виллиса).

По рис. 61 передаточное отношение: при неподвижном жестком колесе

(36)

где и — угловые скорости волнового генератора и гибкого колеса; , — числа зубьев жесткого и гибкого колес; С — число волн;

при неподвижном упругом колесе

(37)

В формуле (36) знак «минус» указывает на разные направления вра­щения генератора и гибкого колеса.

Причины выхода из строя и критерии работоспособности. В процес­се работы этой передачи наблюдается

- разрушение подшипника генератора волн от нагрузки в зацеплении;

- проскакивание генератора волн при больших вращающих моментах, когда зубья на входе в зацепление упираются друг в друга вершинами;

- поломка гибкого колеса от трещин усталости (особенно при u < 80);

- износ зубьев на концах;

- пластические деформации боковых поверхностей зубьев при перегрузках.

Расчёт волновых зубчатых передач отличается от расчёта обычных зубчатых передач тем, что учитывается деформация гибкого венца и генератора.

За критерий работоспособности обычно принимают допускаемые напряжения смятия

;

,

где – коэффициент ширины гибкого венца; d – делительный диаметр гибкого венца.

Волновые передачи можно применять в качестве редукторов, диффе­ренциалов и вариаторов скорости.

Вопросы для самопроверки

- Каковы основные достоинства и недостатки зубчатых передач по сравнению с другими передачами?

- По каким признакам классифицируют зубчатые передачи?

- Чем отличается закрытая передача от открытой?

- Перечислите достоинства зубчатой передачи по сравнению с фрикционной передачей.

- Почему в зубчатых передачах сохраняется постоянным передаточ­ное отношение?

- Что такое эвольвента окружности и какими свойствами, полезными для зубчатых зацеплений, она обладает?

- Какие окружности называют начальными, какие делительными?

- Что называется шагом, модулем и углом зацепления?

- Что такое исходный профиль рейки эвольвентного зацепления?

- В чем сущность основной теоремы зацепления?

- Что такое эвольвента окружности и какими свойствами она обладает?

- Почему эвольвентное зацепление имеет преимущественное применение?

- Что называют полюсом зацепления, линией зацепления и углом зацепления?

- Как определить на линии зацепления точки, соответствующие началу и концу зацепления одной пары зубьев?

- Каков стандартный исходный контур инструментальной рейки эвольвентного зацепления?

- В чем сущность нарезания зубьев методом копирования и методом обкатки? Их сравнительная характеристика?

- Какие окружности зубчатых передач называют начальными и какие окружности зубчатых колес называют делительными? В каких зубчатых передачах они совпадают?

- Что понимают под коэффициентом торцового перекрытия? Как влияет его величина на работу зубчатой передачи?

- Каково влияние числа зубьев на их форму и прочность?

- Как возникает подрезание зубьев при нарезании их инструментом реечного типа?

- Что понимают под зубчатым зацеплением со смещением (модифицированным) и для чего его применяют?

- Какие два вида модификации передач применяют и как их осуществляют?

- Какие факторы влияют на выбор степени точности зубчатых передач? Какие степени точности передач применяют в общем машиностроении? Какие нормы характеризуют степень точности? Для чего необходим боковой зазор в зубчатой передаче?

- С какой целью производят смазывание зубчатых передач?

- В чем сущность картерного смазывания зубчатых передач?

- Какие основные факторы влияют на КПД зубчатых передач?

- Каковы области применения прямозубых и косозубых передач?

- Уточните основное условие для обеспечения постоянства передаточного числа зубчатой передачи.

- Каковы сравнительные достоинства прямозубых и косозубых колёс?

- Как определяется передаточное отношение и передаточное число?

- Каковы главные виды разрушений зубчатых колёс?

- Какие силы действуют в зубчатом зацеплении?

- Какие допущения принимаются при расчёте зубьев на контактную прочность?

- По какой расчётной схеме выполняется расчёт зубьев на изгиб?

- Где применяются прямозубые цилиндрические передачи?

- Каким образом в прямозубой передаче можно уменьшить контактные напряжения?

- Какие напряжения: или — лимитируют работоспособность цилиндрических зубчатых передач и в каких случаях?

- Какие преимущества и недостатки дает увеличение модуля зуба?

- Какие зубья прочнее на изгиб — колеса или шестерни?

- Почему для изготовления шестерни берут более твердый материал, чем для изготовления колес? В каких случаях это обосновано?

- Почему в шевронных передачах угол наклона зубьев выше, чем в косозубых?

- По какой причине ограничивают угол наклона зубьев в косозубых передачах?

- Почему косозубые передачи прочнее, чем прямозубые?

- Чем вызвана плавность работы косозубых передач?

- Какими преимуществами обладают конические колеса с круговыми зубьями по сравнению с прямозубыми?

- Какими методами производится расчет конических передач?

- В чем разница между направлением сил в конических передачах прямозубых и с круговым зубом?

- Что такое эквивалентные и биэквивалентные цилиндрические прямозубые колеса?

- Почему конические передачи с круговым зубом считаются технологичнее прямозубых?

- В каких случаях применяют конические зубчатые передачи?

- Каковы преимущества косозубых цилиндрических передач по сравнению с прямозубыми?

- Как влияет на работу косозубой передачи изменение угла наклона зубьев? Рекомендуемые значения этих углов. Почему ограничивают максимальное значение угла наклона зуба?

- Какие модули зацепления различают для косозубых колес и какова зависимость между ними? Какой модуль стандартизован?

- От каких факторов зависят направления окружной и осевой силы в косозубой передаче?

- Изменение каких параметров зубчатых колес влияет на их контактную прочность?

- В каких случаях применяют шевронные зубчатые колеса, и какими достоинствами они обладают по сравнению с косозубыми? Каковы недостатки шевронных передач?

- Какие рекомендуются углы наклона зубьев шевронных колес и почему допускается их большая величина, чем у косозубых?

- Какими достоинствами обладают конические колеса с круговыми зубьями по сравнению с прямозубыми?

- Является ли модуль зацепления постоянной величиной для конических зубчатых колес?

- По какому сечению зуба производят расчет на изгиб конических колес? Какой модуль характеризует размеры этого сечения?

- Как направлены осевые силы, действующие в зацеплении конических передач?

- Что понимают под эквивалентным цилиндрическим колесом? Как вычисляют эквивалентные числа зубьев для конических колес и для косозубых цилиндрических колес?

- Какое минимальное число зубьев допускается для шестерни цилиндрической и конической передач?

- Какое максимальное передаточное число рекомендуется для одной пары различных видов зубчатых передач?

- В чём заключаются достоинства и недостатки планетарных передач?

- Для чего созданы волновые передачи и в чём заключается принцип их работы?

- В чём заключаются достоинства и недостатки волновых передач?

- Чем волновые передачи отличаются от планетарных?

- От чего зависит передаточное отношение волновых передач?

- В каком случае входной и выходной валы волновой передачи вращаются в разные стороны?

- Какое колесо является ведомым при передаче вращения через герметичную стенку?

- Что такое гибкий подшипник?

- Какая деталь волновой передачи наиболее уязвима?

- Какой формы зубья у волновых передач?

- Каковы устройство и принцип действия волновой передачи?

- От каких параметров зависит передаточное отношение волновой передачи и чем ограничиваются его max и min?

- Каковы особенности преобразования движения в зубчатой и фрикционной волновых передачах?

- По каким условиям выбирают профиль и размеры зубьев в волновой передаче?

- Каковы основные критерии работоспособности и расчета волновых передач?

- Каковы преимущества и недостатки волновых передач и области их применения?

- Как устроена и как работает волновая зубчатая передача? Назовите основные элементы передачи?

- Каковы основные достоинства и недостатки волновой передачи по сравнению с другими передачами?

- Каким образом гибкому колесу придают овальную форму? Как происходит передача движения в волновой передаче от ведущего звена к ведомому?

- Какова разность чисел зубьев жесткого и гибкого колес волновой передачи? Какой применяют профиль зубьев?

- Как вычисляют передаточное число волновой передачи?

- Почему подшипник кулачкового генератора называют гибким?

- Почему волновые передачи применяют в устройствах с повышенными требова­ниями к кинематической точности или к герметичности?

- Сравните волновую передачу с обычной зубчатой с точки зрения коэффи­циента перекрытия зубьев.

- Влияет ли на работоспособность волновой передачи точность изготовле­ния деталей генератора волн?

- Для чего созданы зацепления Новикова и в чём заключается принцип конструкции их зубьев?

- В чём заключаются достоинства и недостатки зацеплений Новикова?

- Назовите достоинства и недостатки зубчатой передачи с зацеплением Новикова и сравните с зубчатой передачей с эвольвентным зацеплением?

- Планетарные передачи — устройство и кинематика, оценка и применение?

- Силы в зацеплении планетарной передачи и особенности расчета на прочность?

- По каким условиям выбирают числа зубьев колес планетарной передачи?

- Какую зубчатую передачу называют планетарной? Ее устройство и принцип работы?

- В каком случае планетарную передачу называют дифференциальной?

- Каковы основные достоинства и недостатки планетарных передач по сравнению с обычными зубчатыми?

- В каких областях машиностроения широко применяют планетарные передачи и почему?

- Какой метод применяют при выводе формулы для определения передаточного числа планетарной передачи?

- В чем заключаются условия соосности, сборки и соседства планетарных передач? Почему расчет планетарных передач начинают с подбора чисел зубьев?

- По какой частоте вращения вычисляют окружную скорость для назначения степени точности передачи и выбора коэффициентов и ?

- Что учитывает коэффициент в формуле определения допускаемых напряжений изгиба для зубьев сателлита?

- Почему в планетарном редукторе центральная шестерня выполнена плавающей?

- Каковы особенности различных типов планетарных передач?

- Почему КПД планетарных передач увеличивается при стремлении передаточного отношения к единице?

- Какие из планетарных передач имеют максимальное передаточное отношение?

- С какой целью применяется самоустановка колес планетарной передачи?

- Что такое дифференциальная передача и каковы ее особенности?

- Какие опоры планетарных передач нагружены больше всего и почему?

- Какой параметр планетарной передачи определяется при проектном расчете? Какое передаточное число используется при этом?

- Каковы условия собираемости планетарных передач?

- Сколько степеней точности зубчатых передач и какова их зависи­мость от окружных скоростей?

- В чем состоит модификация зубчатых зацеплений?

- Какие виды модификаций применяют в цилиндрических и конических зубчатых передачах?

- Каковы материалы и виды термообработки для цилиндрических и конических зубчатых колес?

- Какие способы изготовления цилиндрических зубчатых передач вы знаете?

- Каковы способы изготовления конических зубчатых передач?

- На рисунке показана схема нарезания зубьев конического колеса на зубострогальном станке. Как называется этот способ обработки зубьев?

- Назовите наиболее распространенные в машиностроении конструкции зубчатых колес. В каких случаях применяют сварную конструкцию зубчатого колеса?

- Можно ли применить для изготовления пары зубчатых колес разный ма­териал, например текстолит и сталь?

- Как условно делят зуб на две части - головку и ножку?

- Какие материалы и виды термической обработки применяют для изготовления зубчатых колес?

- Почему стальные зубчатые колеса условно делят на две группы в зависимости от твердости рабочих поверхностей зубьев?

- В чем сущность усталостного разрушения зубьев? Виды разрушения? Меры по предупреждению усталостной поломки зубьев?

- Почему в закрытых передачах усталостное выкрашивание является основным видом разрушения рабочей поверхности зубьев? Меры по предупреждению выкрашивания?

- Почему заедание преимущественно наблюдается в высоконагруженных и высокоскоростных передачах, в чем его сущность? Меры по предупреждению заедания?

- В каких случаях появляется повышенное изнашивание зубьев, и как оно сказы­вается на работе передачи? Меры по предупреждению изнашивания?

- Как в расчетах на прочность зубчатых передач учитывают переменный режим нагружения? Что такое циклограмма вращающих моментов?

- Что влияет на величину допускаемых напряжений для зубчатых колес при расчетах на контактную и изгибную прочность?

- Как определяют допускаемое контактное напряжение для расчетов на прочность передач с непрямыми зубьями?

- Каков физический смысл коэффициентов нагрузки при расчете зубчатых передач на контактную и изгибную прочность?

- От чего зависит коэффициент неравномерности распределения нагрузки по длине контактных линий, как его выбирают?

- От чего зависит коэффициент внутренней динамики нагружения, и как его выбирают?

- От чего зависит коэффициент распределения нагрузки между зубьями, и как его определяют?

- Как определяется модуль зубьев? Могут ли иметь разный модуль шестер­ня и колесо в одной паре зубчатых колес? А у двух пар?

- Можно ли увидеть на зубчатом колесе (см. рис.) линию зацепления NN и угол зацепления или это только теоретически представляемые геометри­ческие элементы?

- Какой профиль зуба получил наибольшее распространение в машиностроении?

- В каких случаях наблюдается подрезание зубьев?

- Покажите на рисунке положительное и отрицательное смещение инст­румента. Опишите результаты положительного смещения.

- Перечислите основные внешние признаки, характеризующее нарушение нормального работоспособного состояния зубчатой передачи.

- К какому виду разрушения может привести действие на зуб переменной нагрузки?

- Какие конструктивные мероприятия можно рекомендовать для повыше­ния сопротивления зубьев на излом?

- Как увеличить сопротивляемость зубьев выкрашиванию рабочих поверхно­стей?

- Для условия = 24, = 36°52'12" выберите из табл. 6 коэффициент формы зуба .

- Выходит ли из строя передача по причине изнашивания зубьев? Как уменьшить изнашивание зубьев?

- Можно ли предупредить заедание зубьев?

- Как располагаются оси вращения валов у цилиндрической прямозубой пе­редачи?

- Определите модуль зубчатого колеса с числом зубьев пo известным , , , .

- Выведите формулы для определения и при известных и .

- Как определяются в формуле коэффициенты , , ?

- В каком случае проводят проверочный расчет зубчатой передачи на изгиб?

- Проанализируйте формулы и определите, в каких зубьях (шес­терни или колеса) возникают большие изгибающие напряжения и почему?

- В каких единицах необходимо подставить и в формулу , что­бы модуль т получить в миллиметрах.

- Расшифруйте формулу и подставьте единицы измерения парамет­ров, входящих в эту формулу.

- В каких зубьях {шестер­ни или колеса) возникает большее нормальное контактное напряжение?

- Будет ли возникать осевая сила в переда­че, состоящей из зубчатых колес (рис.)? Чем отличается эта передача от косозубой?

- Определите и , если известны делительный диаметр и межосевое расстояние.

- Почему в шевронной передаче (см. рис.) осевая сила равна нулю?

- По рисунку определите, как расположены оси валов у винтовой передачи.

- Как влияет угол наклона зубьев на величину осевой силы (см. рис.)?

- При одних и тех же силовых параметрах передачи косозубая передача по сравнению с прямозубой имеет меньшие или большие габариты?

- Как учитывается при расчете зубьев на контактную прочность концен­трация нагрузки и динамичность ее действия?

- Какое допускаемое напряжение следует подставить в формулу — для материала шестерни или материала колеса?

- Запишите формулы проектировочного расчета для открытой косозубой передачи.

- С какими зубьями выполнены шестерня и колесо, показанные на рисунке?

- По какому модулю производят расчет геометрических параметров и по какому модулю — расчет на прочность конической передачи?

- Для = 72, = 75°58’ выберите из табл. 6 коэффициент формы зуба и концентрации напряжений.

- Для чего в формулу введен коэффициент ? Имеется ли он в аналогичных формулах для проектного расчета зубьев на изгиб прямозубой и косозубой передач?

- Каким образом можно снизить нормальное контактное напряжение в пе­редаче, не изменяя силовых параметров передачи и передаточного числа?

- Какие профили зубьев имеют распространенное применение в машино­строении?

- Основное конструктивное отличие зуба Новикова от известных.

- Перечислите недостатки и основные достоинства зубчатых передач с за­цеплением Новикова.

- Вспомните формулы расчета на контактную прочность цилиндрической эвольвентной прямозубой передачи.

- Какие профили зубьев применимы для планетарной зубчатой передачи?

- Перечислите примеры возможного применения планетарных передач.

- Объясните, почему для планетарной передачи (см. рис.) достаточно рассчитать только внешнее зацепление?

- Какие параметры определяются в проектировочном расчете на кон­тактную прочность передач?

- В каких случаях применяют цилиндрические прямозубые передачи?

- Какой физический смысл коэффициентов и нагрузки при расчете зубчатых передач на контактную и изгибную прочность?

- Как из формулы Герца выводят формулу для расчета рабочих поверхностей зубьев на контактную прочность? Что учитывают коэффициенты , и , входящие и формулу?

- От каких параметров стальной прямозубой передачи зависят контактные напряжения? Как можно уменьшить величину контактных напряжений?

- Как влияет на размеры передачи коэффициент ширины венца ?

- Какие допущения принимают при выводе расчетной формулы для проверки зубьев на прочность при изгибе?

- Почему коэффициент , называют коэффициентом формы зуба и концентрации напряжений? От каких параметров зависит его величина?

- Каково условие равной прочности на изгиб зубьев шестерни и колеса?

- Почему ширину венца шестерни делают больше ширины венца колеса?

- Как влияет число зубьев шестерни на работу передачи?

- Какие рекомендации принимают во внимание при выборе модуля зацепления?

- Основные геометрические параметры зубчатых передач. Как они между собой связаны?

- Скольжение в зацеплении? Как оно распределяется по профилю зуба?

- Коэффициент торцового перекрытия ? Как с ним связано распределение нагрузки по профилю зуба?

- Понятие о степенях точности зубчатых передач и их влияние на качественные характеристики передач?

- Контактные напряжения? Какие виды разрушений связаны с этими напряжениями?

- Критерии работоспособности и виды разрушения зубьев зубчатых передач? С ка­кими напряжениями они связаны?

- Понятие о расчетной нагрузке зубчатых передач? Основные факторы, влияющие на коэффициент концентрации нагрузки и коэффициент динамической нагрузки ?

- Силы в зацеплении цилиндрической прямозубой передачи?

- Расчет прочности зубьев цилиндрической прямозубой передачи по контактным напряжениям (вывод формулы для )?

- Как влияют модуль и число зубьев на контактные напряжения?

- Как влияет ширина колеса на контактные напряжения и почему ее ограничивают?

- Как влияет корригирование зубьев на контактные напряжения?

- Расчет прямозубой цилиндрической передачи по напряжениям изгиба (вывод формулы для )?

- Коэффициент формы зуба ? От каких параметров и как зависит его величина?

- Особенности расчета косозубых (шевронных) передач? Чем объясняется повыше­ние нагрузочной способности этих передач по сравнению с прямозубыми? При­чины плавности и бесшумности работы? Приведение косозубого колеса к эквивалентному прямозубому (эквивалентные параметры и )?

- Силы в зацеплении косозубой цилиндрической (шевронной) передаче?

- Особенности расчета косозубых передач по напряжениям изгиба? Как учитывает­ся многопарность зацепления и наклон линии контакта к основанию зуба?

- Конические зубчатые передачи, их оценка по сравнению с цилиндрическими? Области применения? Основные геометрические параметры конической пере­дачи?

- Силы в зацеплении прямозубой конической передачи?

- Приведение конического зубчатого колеса к эквивалентному цилиндрическому (эквивалентные параметры и )?

- Чем отличаются расчетные формулы для и в конических передачах по сравнению с цилиндрическими и почему?

- Какие формы непрямых зубьев применяют в конических передачах и как оцени­вают их преимущества в расчетных зависимостях для и ?

- По каким критериям распределяют передаточное отношение по ступеням многоступенчатой передачи?

- Какие потери определяют КПД зубчатой передачи, и какова его приближенная величина?

- Какие материалы и виды термической обработки применяют для повышения прочности и долговечности зубчатых передач?

- От каких характеристик материала преимущественно зависят сопротивление контактной усталости и допускаемые контактные напряжения?

- Как учитывают переменность режима нагрузки при определении допускаемых напряжений?

- Как записывают условие суммирования повреждений и как его объясняют?

- Что такое типовые режимы нагружения?

- По каким параметрам оптимизируют конструкцию зубчатых передач? Что при­нимают за обобщенный критерий оптимизации?

- Какие из цилиндрических и конических зубчатых передач применяют для передачи вращения между валами, оси которых скрещиваются?

- Какое основное отличие зубчатой пере­дачи от фрикционной?

1. Постоянство передаточного числа

2. Непостоянство передаточного числа

- Движение в зубчатых передачах передается за счет…

1) зацепления зубьев

2) сил трения между зубьями

3) прижатия колес друг к другу

4) скольжения зубьев друг по другу

- В цилиндрических зубчатых передачах передаточное отношение …

1) постоянное

2) переменное

3)

4)

- Минимальное число зубьев прямозубых зубчатых колес по условию отсутствия подрезания равно …

1)

2)

3)

4)

5)

- Зацепление зубчатых колес эквивалентно качению без скольжения окружностей называемых …

1) делительными окружностями

2) начальными окружностями

3) окружностями вершин зубьев

4) основными окружностями

5) окружностями впадин зубьев

- У зубчатых колес находящихся в зацепление должны быть одинаковыми …

1) делительные диаметры

2) ширина колес

3) числа зубьев

4) модули

- Стандартизированным параметром зубчатых колес является …

1) число зубьев

2) угол наклона зубьев

3) делительный диаметр

4) модуль зацепления

5) шаг зубьев

- В зубчатой передаче напряжения изгиба вызывают … зубьев.

1) усталостное выкрашивание

2) поломку

3) износ

4) заедание

- Основными критериями работоспособности зубчатых передач являются …

1) прочность при срезе зубьев

2) контактная прочность зубьев

3) прочность при смятии зубьев

4) прочность при изгибе зубьев

- В зацеплении косозубой цилиндрической передачи действуют силы …

1) радиальная, окружная,

2) радиальная, осевая, нормальная

3) радиальная, окружная, нормальная

4) радиальная, окружная, осевая

- Как классифицируется по взаимному расположению осей колес передача на рисунке?

1. Оси параллельны

2. Оси пересекаются

3. Оси скрещиваются

- Как называется способ обработки зубьев, показанный на рисунке?

1. Фрезерование дисковой фрезой

2. Фрезерование червячной фрезой («обкатка»)

3. Шевингование

4. Притирка

- Как классифицируется по способу изго­товления заготовки зубчатое колесо, на рисунке?

1. Кованое

2. Штампованное

3. Бандажированное

4. Сварное

- Применяются ли (как правило) в общем машиностроении для изготовления зуб­чатых колес бронза, латунь?

1. Да

2. Нет

- Как называется деталь, изображенная на рисунке?

1. Зубчатое колесо цилиндрическое

2. Зубчатое колесо коническое

3. Червячное колесо

- Как называется деталь 1, изображенная на рисунке?

1. Червяк

2. Шестерня

3. Колесо зубчатое

4. Звездочка

5. Шкив

- Как называется окружность (см. рис.), диаметр которой D 140 мм?

1. Начальная окружность

2. Окружность вершин зубьев

3. Делительная окружность

4. Окружность впадин

- Как называется окружность (см. рис.), диаметр которой D 130 мм?

1. Окружность ступицы колеса

2. Окружность впадин

3. Окружность вершин зубьев

4. Делительная окружность

- Напишите формулу для определения моду­ля зубчатого зацепления

1.

2.

3.

- Что называется полюсом зацепле­ния?

1. Точка касания двух соседних зубьев

2. Отношение числа к к шагу зацепления

3. Точка касания делительных (или начальных) ок­ружностей шестерни и колеса

4. Точка касания линии зацепления с основной ок­ружностью шестерни или колеса

- Покажите на рисунке активную линию зацепления (рабочий уча­сток)

1. Отрезок АД

2. Отрезок ВС

3. На чертеже не показан

- Какой профиль имеют зубья пе­редачи, показанной на рисунке?

1. Эльвовентный

2. Циклоидальный

3. Зацепление Новикова

4. Эти профили в машиностроении не используются

- Определить, сколько пар зубьев находится одновременно в зацеп­лении, если = 1,7

1. В течение 70% времени в зацеплении находятся две пары, а в течение 30% времени — одна

2. В течение 30% времени в зацеплении находятся две пары, а в течение 70% — одна

- Какой угол зацепления принят для стандартных зубчатых колес, нарезанных без смещения

1) 15

2) 20

3) 25

4) Любой

- Что называется корригированием?

1. Дополнительная обработка поверхности зуба с це­лью улучшения зацепления по профилю зуба

2. Улучшение свойств зацеплений путем очерчивания рабочего профиля зубьев различными участками эвольвенты той же основной окружности

3. Способ, применяемый для увеличения долговечно­сти зубчатых колес при изнашивании и заедании

- Какое минимальное число зубьев должна иметь некорригированная прямозубая шестерня, чтобы при нарезании ее гребенкой зубья по­лучились неподрезанными?

1) 13

2) 17

3) 21

4) 24

5) 30

- Как изменяется основание ножки зуба при отрицательном смещении рейки?

1. Утолщается

2. Утоньшается

- Определите вид разрушения для зуба, показанного на рисунке участок под буквой а)

1. Поломка зубьев

2. Выкрашивание

3. Изнашивание

4. Заедание

- Для каких видов разрушений зубь­ев разработаны методы расчета на контактную прочность?

1. Поломка

2. Выкрашивание

3. Изнашивание

4. Заедание

- По отпечатку зуба на рисунке в М 1:1 определить модуль зацеп­ления (мм)

1) 6,0

2) 4,5

3) 3,0

4) 2,5

5) 4,0

- Рассчитать диаметр вершин зубьев (мм) ведомого колеса прямозу­бой передачи, если z₁ = 20; z₂ = 50; т = 4 мм

1) 88

2) 208

3) 80

4) 200

5) 190

- Рассчитать межосевое расстояние (мм) прямозубой передачи, если z₁ =20; и = 2; т = 5 мм

1) 300

2) 150

3) 100

4) 200

5) 40

- Покажите на рисунке диаметр впадин зубьев шестерни

1. d_a2

2. d_a1

3. d₁

4. d_f1

5. D₁

- По какой окружности (см. рис.) обычно измеряют шаг зубьев

1. d_a1

2. d₂

3. D₂

4. d_a2

5. d₁

- При проектном расчете размеры открытой зубчатой передачи определяют расчетом …

1) на прочность при изгибе зубьев

2) на прочность при срезе зубьев

3) на контактную прочность зубьев

4) на прочность при смятии зубьев

5) на прочность при сжатии зубьев

- Формула для проектного расчета цилиндрических зубчатых передач имеет вид …

1)

2)

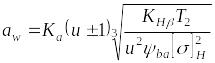
3)

4)

- Формула для проверочного расчета контактных напряжений цилиндрических зубчатых передач имеет вид …

1)

2)

3)

4)

- Формула для проверочного расчета напряжений изгиба цилиндрических зубчатых передач имеет вид …

1)

2)

3)

4)

- По какой формуле производят проекти­ровочный расчет прямозубой передачи на изгиб?

1.

2.

- Как называется коэффициент, обозначае­мый буквой ?

1. Формы зуба

2. Длина зуба

3. Расчетной нагрузки

4. Концентрации напряжений

- Определите коэффициент формы зуба ко­леса, если z₂ =150; и = 4

1) 4,26

2) 3,79

3) 3,60

4) 3,63

- По какой формуле определяют допускае­мое напряжение изгиба при односторон­нем направлении вращения ведущего вала?

1.

2.

- По какой формуле проводят проверочный расчет прямозубой передачи на контакт­ную прочность?

1.

2.

3.

4.

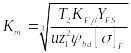
- В каких пределах выбирают коэффициент для прямозубой передачи?

1) 8-40

2) 0,2-1,4

- По какой формуле определяют допускае­мые контактные напряжения?

1.

2.

- Какие передачи рассчитывают на контакт­ную прочность и проверяют на изгиб?

1. Открытые

2. Закрытые

- Покажите на рис. 3.42 нормальный шаг зубьев

1. Х₁

2. Х₂

3. Х₃

4. Х₄

5. На рисунке не показан

- В каких пределах принимают угол наклона зубьев для косозубой зубчатой передачи?

1) 8 ÷ 18°

2) 25 ÷ 45°

3) 20°

4) 90°

- Какой модуль принимают стандартным при расчете косозубой зубчатой передачи?

1. Т_n

2. т_t

3. Оба

- По какому модулю рассчитывают делительный раз­мер в косозубой передаче?

1. Т_n

2. m_y

3. По обоим

- По какой формуле проводят проверочный расчет на контактную прочность косозубой передачи?

1.

2.

3.

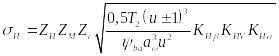
4.

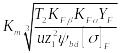
- В каких пределах выбирают коэффициент для косозубой передачи?

1) 10-20

2) 0,2-1,2

3) 0,4-1,0

- Какой модуль в косозубой передаче боль­ше - нормальный или торцовый?

1. m_n

2. m_t

3. Равны

- Определите коэффициент формы и концен­трации напряжений косозубой шестерни, если = 8°40'14"; если Z₂ = 25; d₁ = 40 мм; d₂ = 50 мм

1) 4,07

2) 3,98

3) 3,90

4) 4,03

- По отпечатку зуба (см. рис.) в М 1:1 определите модуль зацепления (мм)

1) 13,5

2) 11,0

3) 7,5

4) 6,0

5) 3,0

- Какой модуль может быть принят стандартным в конической передаче?

1. т_е

2. т_т

3. Оба

- Пользуясь каким модулем рассчитывают диаметр окружности впадин в конической передаче?

1. т_е

2. т_т

3. т_е и т_т

- Чему равна высота (мм) головки зуба, если колесо имеет 45 зубьев (см. рис.); d_e1 = 51 мм, d_e2 = 225 мм?

1) 3,75

2) 11,25

3) 5,0

4) 6,25

5) По этим данным нельзя подсчитать

- Покажите на рисунке диаметр окружности впадин шестерни

1. d_ae1

2. d_e1

3. d_fe1

4. D₁

- По какой формуле проводят проверочный расчет закрытых конических передач на контактную прочность?

1.

2.

3.

- По какому модулю ведется расчет кониче­ского колеса на изгиб?

1. m_e

2. m

3. Можно по m_e и по m

Какая передача показана на рисунке?

1. Зубчатая с внутренним зацеплением

2. Зубчатая планетарная

3. Зубчатая волновая

- Как называют деталь h на рисунке?

1. Водило

2. Сателлиты

- Покажите на рисунке ведущий вал зубчатой передачи

1) 1

2) 2

3) q

4) h

- Достаточно привести расчет на контактную прочность зубьев планетарных передач по рисунку только для зацепления.

1. Внешнего

2. Внутреннего

3. Внешнего + внутреннего

- Влияют ли параметры сателлитов в планетар­ной передаче на значение передаточного числа

1. Влияют

2. Не влияют