3 Проектный расчёт

Межосевое расстояние:

где 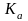= 43 – вспомогательный коэффициент для косозубых передач;

- передаточное отношение ступени;

- вращающий момент на выходном валу передачи;

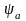= 0,315…0.4 – коэффициент ширины венца колеса;

- среднее допускаемое контактное напряжение;

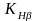= 1 – коэффициент неравномерности распределения нагрузки по длине зуба при симметричном расположении колеса относительно опор.

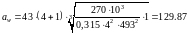(мм)

Принимаем =130 мм

Модуль зацепления

Где к_т =5.8 – вспомогательный коэффициент для косозубых передач;

- делительный диаметр колеса;

- ширина венца колеса;

Получим

_{принимаем} рекомендуемое стандартное значение

Определяем угол наклона зубьев

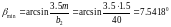
определим суммарное число зубьев шестерни и колеса

Уточняем значение угла наклона зубьев

_{Определим число зубьев шестерни и колеса}

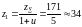
Определим фактическое передаточное отношение редуктора в соответствии с принятыми числами зубьев колес

_{Определим фактическое межосевое расстояние}

Определим размеры колёс

Делительный диаметр

(мм)

(мм)

Проверка

Диаметр вершин зубьев

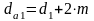
(мм)

(мм)

Диаметр впадин зубьев

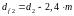
(мм)

(мм)

4 Проверочный расчет цилиндрической передачи редуктора

Проверяем контактные напряжения

где = 376 – вспомогательный коэффициент

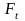- окружная сила в зацеплении;

– коэффициент, учитывающий распределение нагрузки между зубьями;

– коэффициент концентрации нагрузки по длине зуба

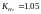– коэффициент динамической нагрузки

– ширина венца зубчатого колеса;

– делительный диаметр зубчатого колеса

Выбора коэффициентов осуществляется в зависимости от окружной скорости колес и степени точности передачи

Окружная сила в зацеплении

где - вращающий момент на тихоходном валу редуктора

(Н)

Окружная скорость колеса:

где - угловая скорость тихоходного вала редуктора

(м/с)

Соответствует 9-я степень точность зубчатых колёс

Перегрузка 2.5%<5%, что в пределах нормы.

Проверим напряжения изгиба зубьев шестерни σ_F1 и колеса σ_F2:

σ_F2 = Y_F2 · Y_β · · K_Fα · K_Fβ · K_Fυ ≤ [σ]_F2;

σ_F1 = σ_F2 · ≤ [σ]_F1,

где K_Fα = 1 – коэффициент, учитывающий распределение нагрузки между зубьями колес;

K_Fβ = 1 – коэффициент неравномерности нагрузки по длине зуба;

K_Fυ = 1,2 – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи;

Y_F1 = 3.75 и Y_F2 = 3,61 – коэффициенты формы зуба шестерни и колеса, определяемые в зависимости от числа зубьев шестерни z₁ и колеса z₂;

Y_β = 0,93 – коэффициент, учитывающий наклон зуба.

Получим:

σ_F2 = 3,61 · 0,93 ·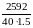 · 1 · 1 · 1,2 = 174.04 МПа < 256 МПа

Получим:

σ_F1 = 174.04 · = 180.8 МПа < 294 МПа.

Условие прочности по напряжениям изгиба выполняются.

Вывод: зубчатая передача редуктора является недогруженной, что находится в пределах допускаемых значений, т.е. условие прочности выполнятся.

5 Определение сил в зацеплении

Окружная сила:

где - вращающий момент на тихоходном валу;

- делительный диаметр колеса.

(Н)

Радиальная сила:

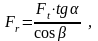
где =20⁰ - угол зацепления;

(Н)

Осевая сила:

(Н)