4.11.2 Основные показатели фильтрования
Процесс фильтрования характеризуется следующими показателями
- скорость
фильтрования
- это объем жидкой фазы (или фильтрата)
V,
прошедший через единицу поверхности
фильтровальной перегородки F
в единицу времени
.
,
;
(4.198)
- удельная
производительность фильтровальной
перегородки
- объем фильтрата V,
проходящий через единицу поверхности
фильтровальной перегородки F.
,
;
(4.199)
- высота (толщина)
слоя осадка
,
м.
Для вывода уравнения,
устанавливающего взаимосвязь между
объемом фильтрата V
и высотой осадка
обозначим буквой Х
объемную концентрацию дисперсных частиц
в суспензии, отнесенную к единице объема
фильтрата. Тогда объем дисперсной фазы
в суспензии определится произведением
.
При фильтровании эта дисперсная фаза,
равномерно распределяясь на поверхности
фильтровальной перегородки F,
образует слой осадка высотой
.
Объем осадка определится как произведение
.
Можно записать
,
(4.200)
откуда
.
(4.201)
4.11.3 Основное дифференциальное уравнение фильтрования
Схема процесса фильтрования суспензии с образованием осадка показана на рисунке 4.66.
1-корпус; 2-суспензия;
3-осадок; 4-фильтровальная перегородка;
5-фильтрат
Рисунок 4.66 – Схема
фильтра для разделения суспензии
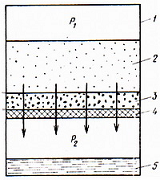простейшем случае фильтр представляет
собой сосуд, корпус 1 которого разделен
на две части фильтровальной перегородкой
4. суспензию 2 помещают в верхнюю часть
сосуда таким образом, чтобы она в течение
всего процесса фильтрования соприкасалась
с фильтровальной перегородкой. В
разделенных частях сосуда создают
разность давлений
,
под действием которой жидкость проходит
через поры фильтровальной перегородки,
образуя фильтрат 5. твердые частицы
задерживаются на поверхности перегородки
4, формируют осадок 3.
Движущая сила
процесса фильтрования
расходуется на преодоление гидравлических
сопротивлений осадка
и фильтровальной
перегородки
.
(4.202)
Осадок представляет собой неподвижный слой твердых частиц, через который движется фильтрат. Поэтому для определения можно воспользоваться формулой Эргуна. Учитывая небольшой размер пор осадка и фильтровальной перегородки (десятые и сотые доли миллиметра) и малую скорость движения фильтрата (обычно – единицы мм/с), можно считать, что фильтрование протекает в ламинарной области. Тогда, пренебрегая вторым слагаемым в уравнении Эргуна и перенося высоту слоя в правую часть равенства, имеем
.
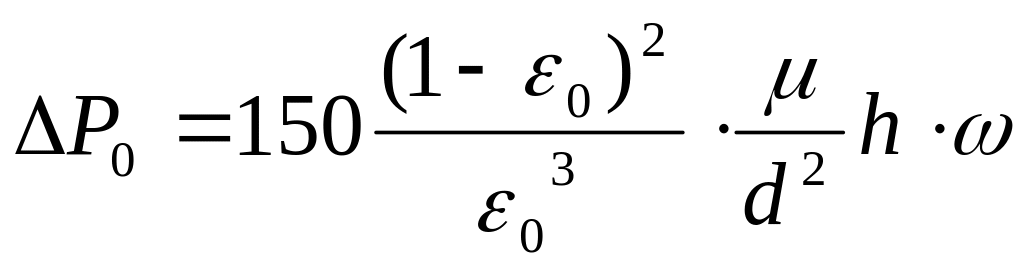(4.203)
Для полидисперсных
промышленных суспензий с частицами
произвольной формы введено понятие
фактора сопротивления осадка
,
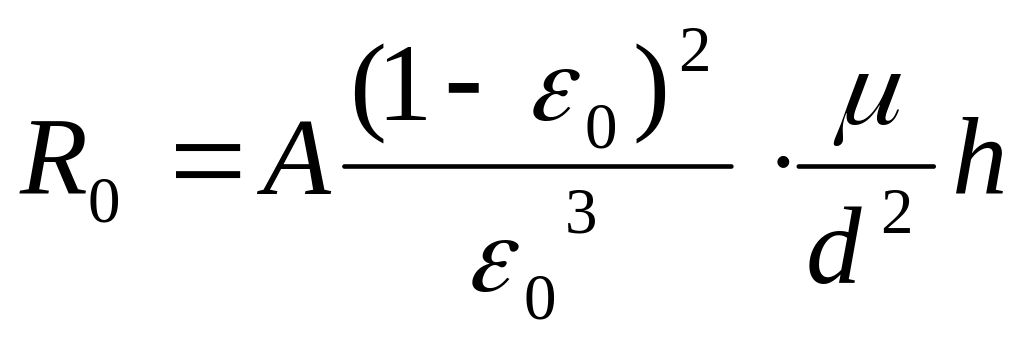(4.204)
где вместо 150 (для сферических частиц одинакового диаметра) поставлен множитель А.
Тогда сопротивление слоя осадка можно выразить уравнением
.
(4.205)
Для фильтровальной перегородки можно записать аналогичное выражение
.
(4.206)
где
- фактор сопротивления фильтровальной
перегородки, определяемый экспериментально.
Учитывая уравнения (4.205) и (4.206), выражение (4.202) принимает вид
,
(4.207)
откуда
.
(4.208)
В ходе процесса
фильтрования сопротивление перегородки
если и изменяется, то незначительно;
поэтому можно считать
постоянной величиной (
).
Фактор сопротивления осадка
(уравнение (4.204)) включает увеличивающуюся
в протекании процесса высоту слоя осадка
h,
поэтому является величиной переменной.
Комплекс постоянных вличин в уравнении
(4.204)
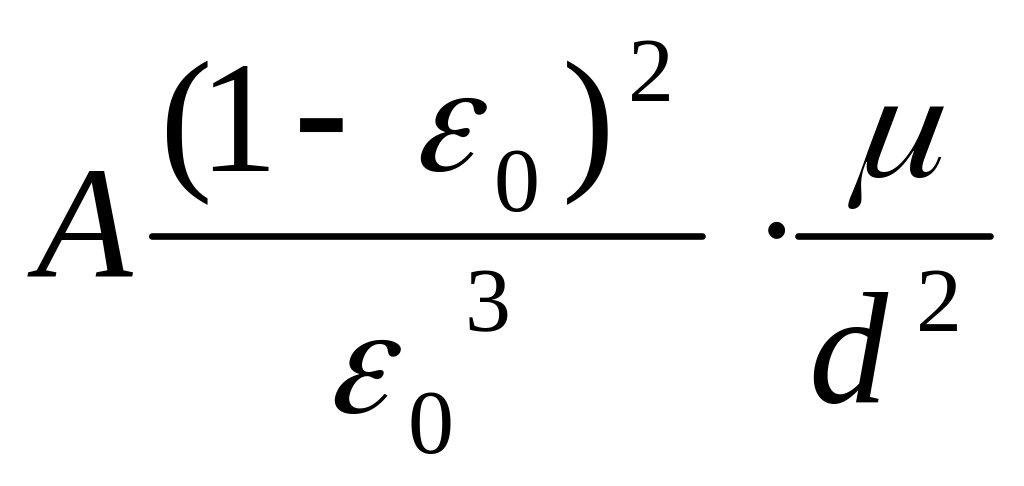называется удельным сопротивлением
осадка и обозначается (как показано
ранее) r,
т.е.
или с учетом уравнения (4.201)
.
(4.209)
Уравнение (4.203) с вводом величины r запишется в виде
,
откуда
.
(4.210)
Последнее выражение показывает, что удельное сопротивление осадка численно равно разности давлений, необходимой для движения фильтрата со скоростью 1 м/с через осадок высотой 1 м.
Определим размерность удельного сопротивления
.
Процесс фильтрования часто проводится в переменном режим – с переменным потоком фильтрата, поэтому изменяющуюся в процессе скорость записывают в виде дифференциального уравнения. Тогда соответственно определению (4.198) с учетом (4.209) можно записать уравнение (4.208) в виде
.
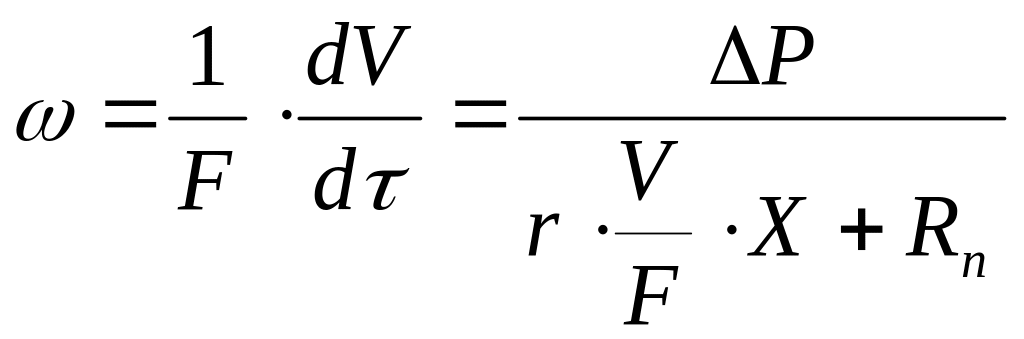(4.211)
Данное выражение называют основным дифференциальным уравнением фильтрования.
В ряде случаев при
фильтровании сопротивление осадка во
много раз превышает сопротивление
фильтровальной перегородки, т.е.
.
Тогда основное дифференциальное
уравнение фильтрования упрощается
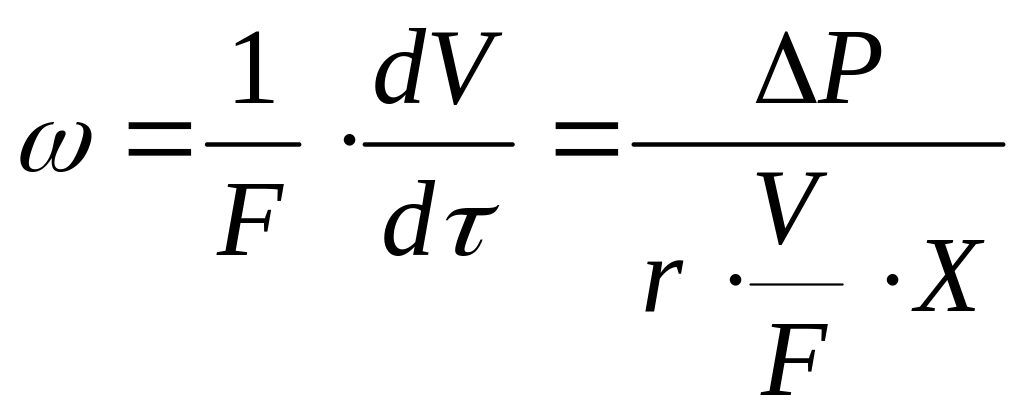
и записывается в виде
.
(4.212)
4.11.4 Режимы фильтрования
Рассмотрим более подробно режимы фильтрования, взяв за основу основное дифференциальное уравнение фильтрования (4.211).
4.11.4.1 Фильтрование при постоянной движущей силе
Разделив переменные
и
дифференциального уравнения фильтрования
(4.211), и учитывая, что
,
получим
.
Интегрируя от
начала процесса (
=0,
V=0)
до промежуточного момента с текущими
значениями
и V
(или до конца
фильтрования
,
),
получим квадратичное выражение
.
(4.213)
Полученное выражение позволяет определить
- продолжительность
фильтрования
для получения на фильтре, рабочая
поверхность которого равна F,
заданного количества фильтрата
.
(4.214)
Иногда необходимо
определить
по накопленному в конце процесса слою
осадка определенной высоты
.
Тогда в уравнение (2.214) величину
надо заменить на
по выражению (4.201)
;
(4.215)
- объем фильтрата, полученного на фильтре поверхностью F за время
;
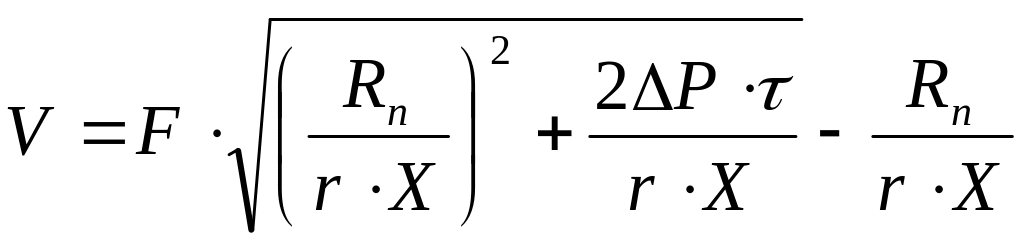(4.216)
- поверхность фильтровальной перегородки (поверхность фильтра), необходимую для получения заданного количества фильтрата V за время
.
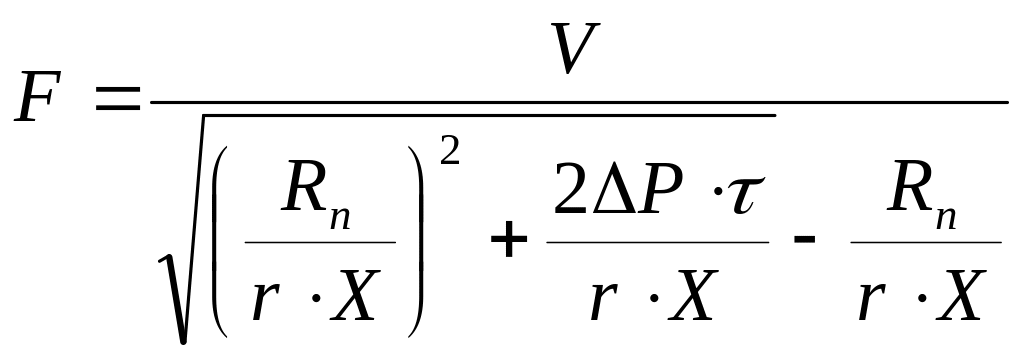(4.217)
Для процесса фильтрования, описываемого уравнением (4.212) (при ) уравнения (4.214)…(4.216) имеют вид
или
;
(4.218)
или
;
(4.219)
.
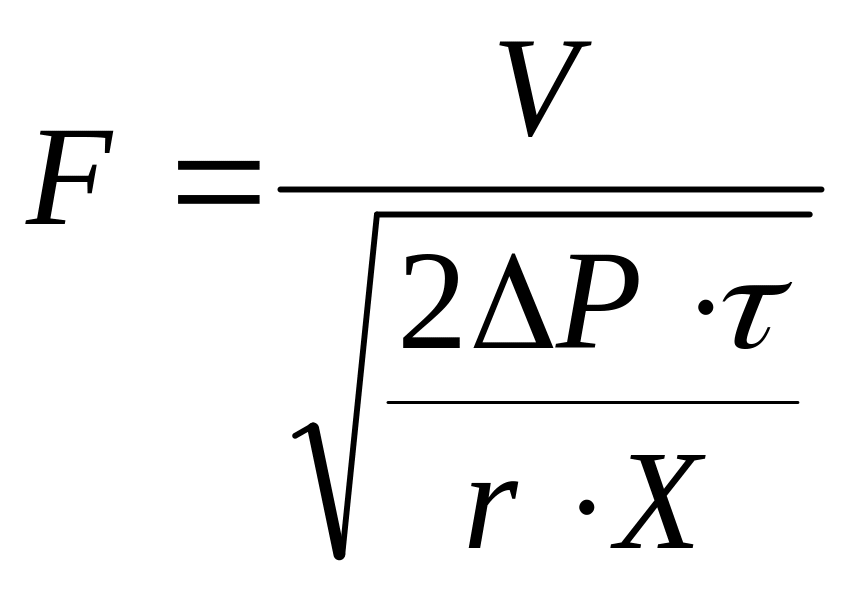(4.220)
Уравнения (4.214)…(4.216) записаны для несжимаемых осадков, для которых удельное сопротивление r есть величина постоянная. Для сжимаемых осадков значение r рассчитывают по уравнению (4.197) и подставляют в соответствующие расчетные уравнения. Например, для уравнения (4.219) получим
;
(4.221)