Раздел 4 гидродинамика и гидродинамические процессы и аппараты

4.1 Основные уравнения гидростатики и гидродинамики

4.1.1 Уравнения Эйлера для гидростатики и гидродинамики

Гидростатика изучает равновесие жидкостей, находящихся в состоянии относительного покоя. При этом форма объема жидкости остается неизменной, силы внутреннего трения отсутствуют.

Для покоящейся жидкости система уравнений Новье-Стокса (выражение 2.58) имеет вид

; ; , (4.1)

и называется системой дифференциальных уравнений равновесия Эйлера.

В случае движения идеальной жидкости ( ) уравнения Новье-Стокса (2.59) позволяют получить систему уравнений

; ; , (4.2)

которые называют дифференциальными уравнениями движения идеальной жидкости Эйлера.

Интегрирование систем выше приведенных уравнений, как и отмечалось ранее (см. раздел 2), позволяет получить основное уравнение гидростатики и уравнение гидродинамики – уравнения Бернулли, которые широко используются в инженерных расчетах.

4.1.1 Основное уравнение гидростатики

Из уравнений (4.1) следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси Z), оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменения вдоль оси X и Y равны нулю. Поскольку частные производные и равны нулю, частная производная может быть заменена на .

Тогда

или (4.3)

Для несжимаемой однородной жидкости . При условии, что , сумму дифференциалов в уравнении (4.3) можно заменить дифференциалом суммы

или . (4.4)

После интегрирования уравнения (4.4) получим

. (4.5)

Уравнение (4.5) называют основным уравнением гидростатики.

Запишем уравнение (4.5) для двух произвольно выбранных горизонтальных плоскостей I-I и II-II (рисунок 4.1).

Т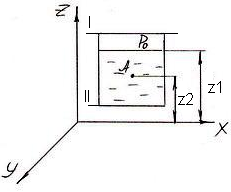 ак как давление в покоящейся жидкости изменяется только по вертикали (т.е. вдоль оси Z), оставаясь одинаковым во всех точках лыбой горизонтальной плоскости, то для любой точки плоскости I-I гидростатическое давление , плоскости II-II - .

Тогда

Рисунок 4.1 - К основному уравнению гидростатики

. (4.6)

Величину Z, характеризующую расстояние данной точки от оси Z (или произвольно выбранной горизонтальной плоскости отсчета) называют нивелирной высотой или геометрическим напором. Она выражается в единицах длины. Действительно

.

Таким образом, по физическому смыслу нивелирная высота представляет собой энергию ( ), приходящуюся на единицу веса (Н) жидкости, т.е. характеризует удельную потенциальную энергию положения данной точки над произвольно выбранной плоскостью сравнения.

Величина называется гидростатическим (или пьезометрическим) напором и по физическому смыслу представляет собой энергию, приходящуюся на единицу веса жидкости, т.е. характеризует удельную потенциальную энергию давления в данной точке.

Согласно основному уравнению гидростатики

сумма удельных потенциальных энергий положения и давления в покоящейся жидкости есть величина постоянная и равная полному гидростатическому напору.

Следовательно, основное уравнение гидростатики является частным случаем закона сохранения энергии.

Переписав уравнение (4.6) относительно , получим

(4.7)

Уравнение (4.7) является выражением закона Паскаля, из которого следует

давление, создаваемое в любой точке покоящейся несжимаемой жидкости, передается во все стороны с одинаковой силой.

Действительно, в соответствии с уравнением (4.8), при изменении давления в точке жидкости на какую-либо величину давление во всякой другой точке жидкости изменится на ту же величину.

Пусть плоскость I-I проходит через свободную поверхность открытого аппарата. Давление над свободной поверхностью жидкости равно атмосферному , т.е. = . Тогда для произвольно выбранной точки А на плоскости II-II абсолютное (или полное) давление в соответствии с выражением (4.7) определится

(4.8)

По рисунку 4.1 , где - глубина погружения в слой жидкости рассматриваемой точки А от свободной поверхности. Тогда

или в общем виде

(4.9)

Абсолютное давление в произвольно выбранной точке покоящейся жидкости равно сумме давления на свободную поверхность и давление столба жидкости с основанием, равным единице, и высотой, равной глубине погружения в слой жидкости рассматриваемой точки.

Уравнение (4.9) является математическим выражением основного закона гидростатики.

Основное уравнение гидростатики позволяет определить давление в аппарате.

Рассмотрим сосуд с жидкостью, к которому на одинаковом расстоянии от плоскости сравнения О-О присоединены две прозрачные трубки (рисунок 4.2,а). Верхний конец у одной из трубок запаян и воздух откачан (давление Р=0); верхний конец другой трубки открыт сверху и на поверхности жидкости будет атмосферное давление.

Под действием абсолютного давления в сосуде (Р) жидкость в трубках поднимается на разные высоты и .

В соответствии с уравнением (4.9) для жидкости в закрытой трубке можно записать

. (4.10)

Полученная высота , называемая высотой давления или приведенной высотой, измеряет абсолютное давление в точке присоединения (т.А на рисунке 4.2), выражая его высотой столба жидкости.

Для жидкости в открытой трубке

. (4.11)

Величина , называемая пьезометрической высотой, измеряет избыточное (превышающее атмосферное) давление в точке А, выраженное высотой столба жидкости.

Таким образом, пьезометрическая высота в отличие от приведенной показывает лишь разность давлений (в данном случае в точке А и атмосферного ).

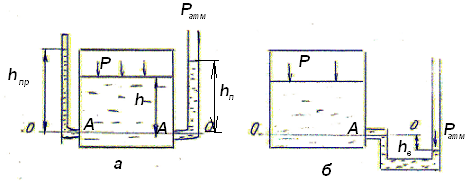
Рисунок 4.2 – Схема замера давления жидкостными приборами (пьезометрами)

Прозрачные трубки, применяемые для определения указанных высот, называются пьезометрами соответственно закрытого и открытого типа.

Если давление над свободной поверхностью в сосуде меньше атмосферного (Р> ), то давление в т.А можно измерить с помощью обратного пьезометра, или вакуумметра, представляющего собой изогнутую трубку (рисунок 4.2,б).

В соответствии с уравнением (4.9) для жидкости в изогнутой трубке можно записать

; . (4.12)

Величина , называемая ваккуметрической высотой, измеряет разность атмосферного и абсолютного давления в точке А, выраженное высотой столба жидкости.

Таким образом, по показаниям пьезометров можно определит соответствующее давление в месте присоединения прибора, выраженное высотой столба жидкости (т.е. единицами длины).

В производственных условиях представляет интерес выражения давления как силы, приходящейся на единицу поверхности. Действующие контрольно-измерительные приборы позволяют определить давление в точке присоединения в технических атмосферах. Одна техническая атмосфера

1 ат = 1 кгс/см = 100 кН/м = 100 кПа.

Слагаемое в уравнении (4.9) показывает превышение давления в точке относительно атмосферного давления и называется избыточным ( ). Тогда

или (4.13)

Избыточное давление измеряет прибор, называемый манометром; поэтому это давление иногда называется манометрическим ( ). Манометр позволяет определить избыточное давление, выраженное в технических атмосферах (кгс/см ). Предположим, что = = 5 кгс/см . Тогда абсолютное давление в соответствии с уравнением (4.13) равно =1+5=6 кгс/см .

Абсолютное давление в аппарате может быть меньше атмосферного . В этом случае уравнение (4.9) имеет вид

, (4.14)

где называется отрицательным избыточным давлением, которое замеряется вакуумметром и называется вакуумметрическим .

В этом случае уравнение (4.14) запишется

или . (4.15)

Например, вакуумметр показывает давление =0,4 кгс/см . тогда абсолютное давление (разрежение) в аппарате =1-0,4=0,6 кгс/см .

4.1.2 Уравнения Бернулли для идеальной и реальной жидкости

Для определения сил, действующих в выделеноом объеме движущейся идеальной жидкости, умножим левые и правые части уравнений Эйлера для гидродинамики (4.2) на соответствующие длины ребер этого объема ( ).

Получим

Но ; ; . Тогда

Просуммировав левые и правые части этих уравнений, получим

(4.16)

В левой части уравнения (4.15)

; ; ,

откуда

В правой части уравнения (4.16) выражение в скобках представляет собой полный дифференциал гидростатического давления dP.

Тогда уравнение (4.16) примет вид

. (4.17)

Так как рассматривается однородная несжимаемая жидкость ( ) и принимается условие , то сумму дифференциалов в уравнении (4.17) можно заменить дифференциалом суммы. Тогда

. (4.18)

Разделив левую и правую часть уравнения (4.18) на произведение и проинтегрировав полученное уравнение, получим

. (4.19)

Уравнение (4.19) называют уравнением Бернулли для идеальной жидкости, в котором Н – общий или гидродинамический напор.

Для любых произвольно выбранных сечений потока значение гидродинамического напора Н должно оставаться постоянным, т.е.

. (4.20)

Два первых слагаемых уравнения Бернулли (4.19) были рассмотрены при анализе основного уравнения гидростатики: - геометрический напор или удельная потенциальная энергия положения; - статический (пьезометрический) напор или удельная потенциальная энергия давления.

Таким образом, сумма характеризует полную удельную потенциальную энергию в данном сечении (точке) и выражается в единицах длины или удельной энергии, т.е. энергии, приходящейся на единицу веса жидкости.

Третье слагаемое уравнения Бернулли (4.19) называют скоростным (динамическим) напором или удельной кинетической энергией в данном сечении (точке) потока.

Уравнение Бернулли (4.19) является частным случаем закона сохранения энергии, так как

для любого сечения или точки потока при установившемся движении идеальной жидкости сумма потенциальной и кинетической энергии жидкости остается величиной постоянной.

В случае горизонтально расположенного трубопровода и уравнение Бернулли для идеальной жидкости упрощается:

. (4.21)

Проиллюстрируем применение уравнения Бернулли на примере потока идеальной жидкости, движущейся через произвольно расположенный в пространстве трубопровод переменного сечения (рисунок 4.3).

П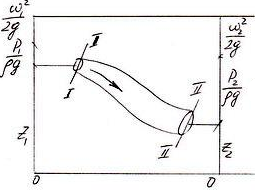 усть для точек, лежащих на оси трубопровода в поперечных сечениях I-I и II-II, нивелирные высоты равны и соответственно. Установим в каждой из этих точек две вертикальные открытые пьезометрические трубки, у одной из которых нижний конец загнут навстречу потоку жидкости в трубопроводе.

Рисунок 4.3 - К уравнению Бернулли для идеальной жидкости

В прямых вертикальных трубках (с незагнутыми нижними концами) жидкость поднимается на высоту, отвечающую гидростатическому давлению в точках их погружения, т.е. эти трубки будут измерять пьезометрические напоры в соответствующих точках.

В трубках с нижними концами, направленными навстречу потоку, уровень жидкости будет выше, чем в соседних вертикальных трубках, так как трубки с загнутыми концами будут показывать сумму пьезометрического и динамического (скоростного) напоров. Однако, согласно уравнению (4.19), во всех трубках с загнутыми нижними концами жидкость поднимается на одну и туже высоту относительно произвольной горизонтальной плоскости сравнения, равную гидродинамическому напору Н (см. рисунок 4.3).

Площадь поперечного сечения II-II трубопровода больше сечения I-I. Поэтому скорость жидкости при данном ее расходе, согласно уравнению неразрывности потока, будет меньше . Соответственно .

В любом поперечном сечении трубопровода скоростной напор можно измерить по разности показаний установленных здесь трубок (с загнутым и прямым нижними концами). Следовательно, эта разность должна быть больше для сечения II-II, чем для сечения I-I. Вместе с тем из уравнения Бернулли следует, что высота уровня жидкости в прямой трубке в сечении II-II должна быть меньше соответствующей высоты в прямой трубке сечения I-I настолько же, насколько скоростной напор в сечении II-II меньше, чем в сечении I-I.

Приведенный пример демонстрирует взаимный переход потенциальной энергии в кинетическую и наоборот при изменении площади сечения трубопровода, а также постоянство суммы этих энергий в любом поперечном сечении трубопровода.

При движении реальных жидкостей начинают действовать силы внутреннего трения, обусловленные вязкостью жидкости и режимом ее движения, а также силы трения о стенки трубы. Эти силы оказывают сопротивление движению жидкости. На преодоление возникающего гидравлического сопротивления должна расходоваться некоторая часть энергии потока. Поэтому общее количество энергии потока по длине трубопровода будет непрерывно уменьшаться вследствие перехода потенциальной энергии в потерянную энергию – затрачиваемую на трение и безвозвратно теряемую при рассеивании тепла в окружающую среду.

При этом для двух любых сечений I-I и II-II трубопровода, расположенных по ходу движения реальной жидкости (см. рисунок 4.3)

При движении реальной жидкости высоты ее подъема (относительно плоскости сравнению) в трубках с концами, обращенными навстречу потоку, уже не будут равны в сечениях I-I и II-II, как было показано на рис.4.3 применительно к движению идеальной жидкости. Разность высот в этих трубках, обусловленная потерями энергии на пути жидкости от сечения I-I до сечения II-II, характеризует потерянный напор .

Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения (4.20) должен быть введен член, выражающий потерянный напор. Тогда получим уравнение Бернулли для реальных жидкостей

. (4.22)

Потерянный напор характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

Потерянный напор включает в себя две составляющих – потери напора на трение и на преодоление местных сопротивлений , под которыми понимают источник изменения направления или сечения потока (повороты, сужения, расширения, вентили и т.д.), т.е.

. (4.23)

Уравнение (4.22) может быть представлено в несколько ином виде, если умножить обе его части на :

. (4.24)

В уравнении (4.24) величина - потерянное давление, равное

. (4.25)

Определение потерь напора или давления является практически важной задачей, связанной с расчетом энергии, которая необходима для перемещения реальных жидкостей при помощи насосов, компрессоров и т.д.

4.2 Гидравлическое сопротивление трубопроводов и аппаратов

Для определения движущей силы гидродинамических процессов, под которой понимается разность давлений между двумя точками или сечениями потока, необходимо знать потерянный напор (см. уравнение 4.22), который складывается из потерь напора на трение и на преодоление местных сопротивлений .

Для определения потерь напора (или давления) на трение применяется уравнение Дарси-Вейсбаха

,м и ,Па (4.26)

где - коэффициент гидравлического трения или просто коэффициент трения, зависящий от гидродинамического режима движения, для ламинарного режима еще и от относительной шероховатости для турбулентного режима.

Основные виды местных потерь напора можно условно разделить на следующие группы:

- потери, связанные с изменением сечения потока (или средней скорости потока). Сюда относятся различные случаи входа жидкости в трубу, выхода жидкости в резервуар, внезапного расширения, сужения, а также постепенного расширения и сужения потока;

- потери, вызванные изменением направления потока. Здесь рассматриваются различного рода повороты, колена, угольники, отводы, используемые на трубопроводах;

- потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы и т.п.);

- потери, связанные с делением или слиянием потоков. Это, например, тройники, крестовины и отверстия в боковых стенках трубопроводов при наличии транзитного расхода.

Величину потерь напора (или давления) на преодоление местных сопротивлений можно определить по выражению

, м ; , Па, (4.27)

где - коэффициент местного сопротивления.

Значение коэффициентов определяется в зависимости от вида местного сопротивления приведены в справочной литературе.

Если система трубопроводов имеет несколько местных сопротивлений, то

, м. (4.28)

Иногда для расчета применяют другой способ, по которому потери напора в местном сопротивлении приравниваются гидравлическому сопротивлению прямой трубы эквивалентной длины

, м, (4.29)

где - эквивалентная длины прямой трубы, имеющей такое же гидравлическое сопротивление, как и рассчитываемое местное сопротивление;

- безразмерный коэффициент, значения которого приводятся в справочной литературе.

В трубопроводе постоянного сечения скорость потока постоянна по длине трубопровода и общий потерянный напор, равный , можно рассчитать по выражению

,м, (4.30)

а потерю давления – по уравнению

, Па. (4.31)

Расчет гидравлического сопротивления аппаратов химической технологии в принципе ничем не отличается от рассмотренного выше расчета гидравлического сопротивления трубопроводов. Обычно в аппаратах наибольший вклад в общие потери напора приходится на долю местных сопротивлений, поскольку в большинстве случаев промышленные аппараты не являются полыми, а заполнены различными материалами (гранулами, насадкой и т.п.) и устройствами (контактными тарелками, мешалками и т.п.), которые существенно и многократно изменяют направление и сечение потоков газа и жидкости при их движении через аппарат. В этих условиях и критические числа критерия Рейнольдса значительно меньше. Например, для аппаратов с насадкой составляет несколько десятков. Все это следует учитывать при гидравлических расчетах аппаратов.

4.3 Основные уравнения движения жидкости

1 Уравнения расхода:

массовый расход , кг/с

объемный расход , м /с

2 Уравнение неразрывности (сплошности) потока

3 Уравнение Бернулли

, м

;

,м;

, м.

4 Гидродинамический режим

;

для труб некруглого сечения .

5 Диаметр трубопровода круглого сечения

,м.

4.4 Физические модели структуры потоков

Структура потоков в технологических аппаратах оказывает существенное влияние на эффективность химико-технологических процессов. Частицы потока движутся по сложным пространственным траекториям, иногда в противоположном относительно основному потоку направлении.

Степень полноты завершения химико-технологического процесса зависит от распределения времени пребывания частиц потока в аппарате, так как некоторые частицы потока могут задерживаться в аппарате (застойные зоны), а другие, наоборот, проскакивать (байпасирование потока), что непосредственно связано с временем контакта и эффективностью массо- и теплообмена.

Распределение времени пребывания частиц потока в аппарате оценивается статическим распределением.

Возможными источниками неравномерности распределения частиц потока по времени пребывания в технологических аппаратах являются

- неравномерность профиля скоростей потока;

- турбулизация потока;

- наличие застойных зон в потоке;

- каналообразование, байпасные и перекрестные токи;

- температурные градиенты движущихся сред;

- тепло- и массообмен между фазами.

Может оказаться, что истинное время пребывания в аппарате частиц потока недостаточно для осуществления процесса, например, диффузии, а от этого зависит эффективность всего диффузионного процесса в целом. Поэтому важным является учет реальной структуры потока в аппарате с помощью модельных представлений о внутренней структуре потоков.

Для процессов массопередачи описание структуры потоков позволяет выяснить вопросы перемещения и распределения компонентов в этих потоках. Поэтому все математические модели потоков записываются в виде уравнений, определяющих изменение концентрации вещества в потоке.

Среднее время пребывания всех частиц потока жидкости в аппарате определяется по выражению

, (4.32)

где - объем рабочей зоны аппарата, м ;

- объемный расход потока, м /с.

4.4.1 Экспериментальное исследование структуры потока

Исследование структуры потоков в реальных аппаратах проводят на экспериментальной установке, одна из схем которой приведена на рисунке 4.4.

1-аппарат; 2-концентратомер; 3-графопостроитель

Рисунок 4.4 – Схема установки для получения кривых отклика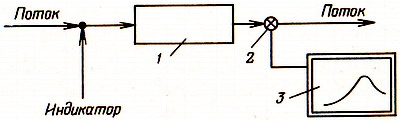

В поток, входящий в аппарат, определенным образом вводят индикатор, а на выходе потока из аппарата замеряют концентрацию индикатора как функцию времени. Эта выходная кривая называется функцией отклика системы на типовое возмущение (сигнал) по составу потока. В качестве индикаторов используют красители, растворы солей и кислот, изотопы и другие вещества. При выборе индикатора необходимо учесть, что поведение частиц индикатора в аппарате должно быть подобно поведению частиц потока.

Индикатор на входе в аппарат вводят в виде стандартных сигналов:

- импульсный – индикатор вводится в поток практически мгновенно, в виде дельта-функции;

- ступенчатый – концентрация индикатора во входящем потоке изменяется скачкообразно от нуля до некоторого значения ( ) и в дальнейшем поддерживается на этом уровне;

- циклический (по закону гармонического колебания).

Для исследования структуры потоков наиболее применимы импульсное и ступенчатое изменение входной величины.

Кривые отклика на стандартные сигналы изображаются в безразмерных величинах:

- безразмерная концентрация (вертикальная ось);

- безразмерное время (горизонтальная ось).

; - концентрация индикатора в потоке соответственно начальная и рабочая, изменяющаяся во времени .

Функция отклика на импульсное возмущение входной величины называется С-кривой, на ступенчатое - F-кривой.

Типичные функции отклика системы на импульсное и ступенчатое возмущение изображены на рисунке 4.5.

Рисунок 4.5 - Типичные функции отклика системы на импульсное возмущение (С-кривая) (b) и ступенчатое возмущение (F-кривая) (d)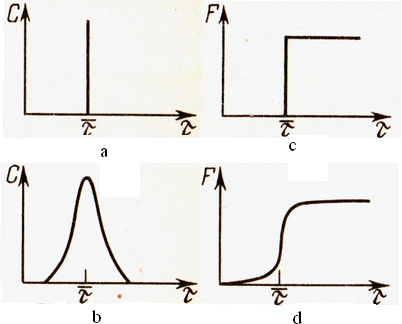

а – импульсный сигнал; с – ступенчатый сигнал.

Из рисунка 4.5 следует, что площадь, ограниченная С-кривой, всегда равна 1; при ступенчатом изменении входной величины значения F-кривой изменяются от нуля до единицы.

Вид С-кривой и F-кривой определяется лишь структурой потока; поэтому вид отклика на стандартные сигналы может достаточно точно отображать реальный физический процесс.

4.4.2 Идеализированные модели гидродинамической структуры потока

Таблица 4.1

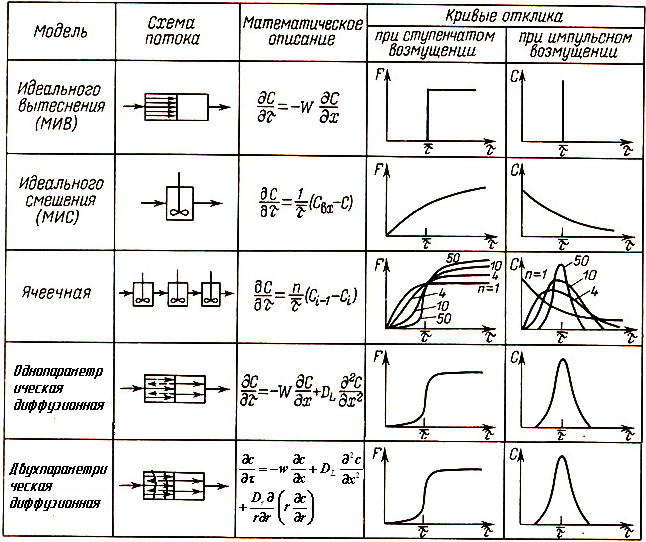
Наиболее простыми математическими моделями потоков являются модели идеального вытеснения и идеального перемешивания. Единственным параметром этих моделей является среднее время пребывания .

Модель идеального вытеснения (МИВ) – теоретическая модель с идеализированной структурой движущегося потока. В соответствии с МИВ принимается поршневое течение без перемешивания вдоль потока при равномерном распределении концентраций вещества в направлении, перпендикулярном движению. При этом время пребывания всех частиц в зоне идеального вытеснения одинаково и равно среднему времени .

Схематичное изображение МИВ, математическое описание и отклики на ступенчатое и импульсное возмущения изображены в таблице 4.1.

Модели идеального вытеснения соответствуют процессы, протекающие в трубчатых аппаратах, у которых отношение длины к диаметру более 20; процессы в трубчатых аппаратах, заполненных зернистым материалом (насадкой, катализатором, адсорбентом и т.д.).

Модель идеального перемешивания (МИП) – представляет идеализированный поток и является теоретической моделью. В соответствии с моделью принимается, что поступающий в аппарат поток мгновенно распределяется по всему объему вследствие полного (идеального) перемешивания частиц среды. При этом концентрация распределенного вещества во всех точках аппарата и в потоке на выходе из него одинакова. В соответствии с представлением МИП можно записать

, (4.33)

где - концентрация индикатора во входящем потоке, кг/м ;

- концентрация на выходе из аппарата, кг/м

- концентрация в любой точке зоны идеального перемешивания, кг/м .

Время пребывания частиц потока в аппарате идеального перемешивания неравномерно: некоторые частицы жидкости в результате, например, действия мешалки сразу попадут к выходу из аппарата и выйдут из него; некоторые частицы надолго задерживаются в аппарате.

Схематическое изображение МИП, математическое описание и отклики на ступенчатое и импульсное возмущение изображены в таблице 4.1.

Наилучшим образом эта модель соответствует реальным потокам в проточных аппаратах с мешалкой, у которых высота мало отличается от диаметра, мешалка создает высокую степень перемешивания, и объемный расход невелик. МИП соответствуют процессы в аппаратах с псевдоожиженным слоем (адсорберы, сушилки и т.д.).

4.4.3 Модели гидродинамической структуры реальных потоков

Структура потоков в реальных аппаратах часто не соответствует идеализированным моделям. Это обусловлено главным образом частичным перемешиванием жидкости, проходящим одновременно с ее поступательным движением. Для описания структуры таких потоков используются ячеечная, одно- и двухпараметрические диффузионные и комбинированные модели.

Ячеечная модель представляет ряд последовательно соединенных ячеек и предполагает идеальное перемешивание в пределах каждой ячейки и отсутствие перемешивания между ячейками. Суммарный объем всех ячеек равен объему реального аппарата ( ). Параметром, характеризующим данную модель, является число ячеек n. Если ячейки имеют одинаковый объем ( ), то число ячеек определится по выражению

. (4.34)

При n=1 ячеечная модель переходит в МИП, при n= ячеечная модель переходит в МИВ. Таким образом, МИП и МИВ являются крайними случаями ячеечной модели.

Схематичное изображение ячеечной модели, математическое описание и отклики на ступенчатое и импульсное возмущение приведены в таблице 4.1.

Однопараметрическая диффузионная модель представляет модель идеального вытеснения, осложненную обратным (или продольным) перемешиванием.

Параметром, характеризующим диффузионную модель, является коэффициент продольного перемешивания (или коэффициент продольной диффузии) . Коэффициент продольного перемешивания учитывает молекулярную и турбулентную диффузию и неравномерность поля скоростей в потоке и считается постоянным по длине аппарата.

Схематичное изображение однопараметрической диффузионной модели, математическое описание и отклики на ступенчатое и импульсное возмущение приведены в таблице 4.1.

Диффузионную модель используют для описания структуры потоков в аппаратах с непрерывным контактом фаз (например, в насадочных и пленочных массообменных колоннах).

Двухпараметрическая диффузионная модель учитывает перемешивание в продольном и радиальном направлении. Эта модель характеризуется коэффициентами продольного ( ) и радиального ( ) перемешивания.

Коэффициентами продольного и радиального перемешивания определяются экспериментальным путем.

Процессы, в которых наблюдаются байпасные и циркуляционные потоки, застойные зоны, не удается описать с помощью рассмотренных ранее моделей. В таких случаях используют комбинированные модели структуры потоков. Комбинированная модель может включать структуры с идеальным перемешиванием, идеальным вытеснением с продольным перемешиванием, байпасные потоки, циркуляционные потоки (рециклы или обратные потоки). При построении комбинированной модели, включающей перечисленные возможные составляющие, необходимо оценить влияние каждого из них на структуру потока в аппарате. Зоны, которые незначительно изменяют гидродинамическую картину, лучше не учитывать. При окончательном решении следует иметь в виду, что с увеличением числа зон различных структур потоков можно описать процесс любой сложности, однако математическое моделирование усложняется настолько, что модель окажется неприемлемой.

4.5 Движение потока через слой зернистого материала

В химической и других отраслях промышленности широко применяются процессы, связанные со взаимодействием газов и слоя мелкораздробленных твердых частиц, находящихся в кипящем, или псевдоожиженном состоянии. Аппараты с кипящим слоем используются для перемещения или смешивания сыпучих материалов, для проведения процессов обжига, теплообмена, сушки, адсорбции, каталитических и других процессов.

4.5.1 Три состояния слоя зернистого материала

Различают три качественно различных состояния слоя зернистого материала, через который проходит восходящий поток газа или жидкости.

При небольших значениях скорости потока последний фильтруется через слой, причем все частицы слоя находятся в соприкосновении друг с другом и в гидравлическом отношении представляют собой пористую среду (рисунок 4.6). В результате движения жидкого или газового потока через поры между зернами имеет место некоторая потеря напора.

Рисунок 4.6 - Неподвижный слой

По мере увеличения скорости потока достигается такое значение её, когда подъемная сила жидкого или газового потока, обусловленная силами трения или инерционными силами, действующими на частицы, становится равной весу слоя частиц и последний оказывается взвешенным в восходящем потоке, а частицы уже не соприкасаются друг с другом. При дальнейшем увеличении скорости потока слой начинает расширяться, а частицы приобретают вихревое движение (рисунок 4.7).

П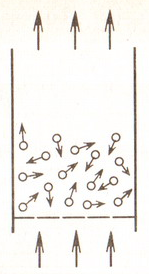 ри достаточно больших скоростях весь слой увлекается восходящим потоком и начинает двигаться вверх, т.е. начинается пневмотранспорт зернистого материала (рисунок 4.8).

В определенных условиях плотный слой может перейти в псевдоожиженный, а последний в транспортируемый и наоборот.

Рисунок 4.7 - Псевдо-ожиженный слой

Рисунок 4.8 - Движущийся слой

4.5.2 Сравнительная характеристика неподвижного и псевдоожиженного слоя

По сравнению с неподвижным псевдоожиженный слой зернистого материала имеет следующие преимущества:

- вследствие интенсивного перемешивания температура и твердые частицы распределяются относительно равномерно. Это может иметь большое значение во многих химических и каталитических процессах;

- так как размер частиц в кипящем слое обычно меньше, чем в неподвижном, то и диффузионные сопротивления в самой частице меньше. Это также может быть благоприятным фактором во многих химических и каталитических процессах;

- в псевдоожиженный слой можно легко вводить твердые частицы и выводить их из него. Здесь упрощается организация непрерывности процесса;

- более высокие коэффициенты теплоотдачи вследствие движения частиц вдоль наружных или внутренних теплообменных поверхностей;

- вследствие интенсивности теплообмена между частицами и газом отработанные частицы во взвешенном состоянии легче отдают тепло, чем более крупные частицы в неподвижных слоях;

- в большинстве случаев при псевдоожижении требуется меньший перепад давления, чем в процессах с неподвижным слоем;

- псевдоожижение исключает необходимость таблетирования катализаторов, представляющего наиболее важную статью расхода во многих каталитических процессах.

Однако псевдоожиженый слой имеет недостатки:

- продольное перемешивание газа или жидкости, а также твердых частиц в кипящем слое. Это приводит к понижению селективности;

- истирание катализатора, что ведет к уменьшению размера частиц псевдоожижаемого материала, т.е. требуется регулирование скорости газа или жидкости;

- псевдоожижение газом возможно только в случае, если в процессе реакции не образуется жидкости;

- оборудование для процессов с кипящим слоем подвергается значительной эрозии. Поэтому требуется специальное и дорогое оборудование;

- благодаря выносу твердых частиц, так называемому уносу, требуются устройства для пылеулавливания;

- истирание и образование пыли приводит к потерям катализатора. Возмещение из влечет за собой значительные затраты.

4.5.3 Основные показатели слоя зернистого материала

Пусть плотный слой зернистого материала представляет собой объем , часть которого занимают непосредственно частицы , а остальную часть занимают образующиеся между частицами извилистые паровые каналы, по которым движется поток газа через слой.

Важнейшей характеристикой слоя является его порозность или доля свободного объема

. (4.35)

Если плотность единицы объема слоя , плотность частиц и газа , то

, (4.36)

откуда

. (4.37)

В случае потока газа или паров и, следовательно, величиной в уравнении (4.37) можно пренебречь; тогда

. (4.38)

Действительную скорость газа в каналах слоя найти трудно. Поэтому ее выражают через скорость, условно отнесенную к полному поперечному сечению слоя или аппарата. Эту скорость, равную отношению объемного расхода жидкости ( ) ко всей площади поперечного сечения слоя ( ), называют фиктивной скоростью или скоростью фильтрации

, м/с. (4.39)

Тогда зависимость между действительной скоростью и скоростью фильтрации выразится соотношением

, (4.40)

где - коэффициент извилистости паровых каналов. Зависит от соотношения длины канала ( ) и высоты слоя H. Так как чаще всего .

Коэффициент извилистости определить сложно. Поэтому принимают =1.

Тогда действительная скорость потока газа в каналах слоя

, м/с. (4.41)

Для гидродинамических расчетов необходимо располагать величиной эквивалентного диаметра парового канала. Эта величина определяется, как отношение учетверенной площади суммарного сечения паровых каналов к смоченному периметру этого сечения, или, что то же самое, как отношение учетверенного свободного объема единицы объема слоя к поверхности всех частиц в том же объеме ,т.е.

. (4.42)

Если слой состоит из гранул шаровой формы одинакового диаметра , то объем одной гранулы равен , а объем всех гранул в 1 м слоя составит м ; следовательно, число гранул в таком слое будет

. (4.43)

Тогда поверхность всех этих гранул будет равна

, (4.44)

где - площадь сферы диаметром .

Следовательно, эквивалентный диаметр парового канала

. (4.45)

Для частиц нешарообразной формы вводится коэффициент формы частиц

, (4.46)

для шара =1;

для куба =0,806.

Многочисленными исследованиями установлено, что поток среды через слой гранулированного материала может иметь ламинарное, переходное или турбулентное движение в зависимости от численного значения параметра Рейнольдса

. (4.47)

Заменяя и подставляя из уравнения (4.45), получим

, (4.48)

где - плотность, кг/м .

Потери напора в слое может быть вычислена по известному уравнению гидравлики

, Па, (4.49)

где - высота слоя, м;

- плотность потока, кг/м ;

- коэффициент гидравлического сопротивления. Считается, что ламинарный режим движения потока наблюдается при ; переходный - ; при - турбулентный.

Некоторые исследователи предлагают для определения следующее уравнение

, (4.50)

причем коэффициент и показатель степени зависят от числа ; при ламинарном движении =1, в переходной области <1 и в турбулентной области =0.

Для всех режимов

. (4.51)

Для турбулентного режима можно принять =2,34.

Заменяя в уравнении (4.49) и подставляя значение из уравнения (4.45), получим

, Па. (4.52)

Для технических расчетов применяется уравнение Эргуна, которое хорошо описывает экспериментальные данные по сопротивлению в слое:

, Па/м. (4.53)

Это уравнение справедливо как для стационарного, так и для движущегося плотного слоя.

Величина в уравнении (4.52) представляет собой относительную скорость движения паров:

, (4.54)

где - скорость движения относительно стенок аппарата паров и гранул слоя, м/сек;

- порозность слоя (знак минус соответствует прямоточному движению паров и слоя, знак плюс – противоточному их движению).

4.5.4 Гидродинамика псевдоожиженного слоя

При восходящем потоке газа через плотный слой зернистого материала с увеличением скорости потока увеличивается сопротивление слоя и ослабляется давление частиц друг на друга. При достижении некоторого критического значения скорости сопротивление слоя становится равным весу слоя, частицы перестают оказывать давление друг на друга и слой переходит во взвешенное состояние; в этих условиях у частиц возникает возможность перемещаться в пределах слоя. Скорость, при которой нарушается неподвижность слоя и он начинает переходить в псевдоожиженное состояние, называют скоростью псевдоожижения или критической и обозначают .

Рассмотрим графическую зависимость перепада давления (гидравлического сопротивления) , порозности слоя и степени расширения слоя от скорости газа, по оси абсцисс на этом графике отложено отношение скорости газа к критической скорости , при которой слой переходит во взвешенное состояние; это отношение принято называть числом псевдоожижения , т.е.

. (4.55)

Число псевдоожижения характеризует интенсивность перемешивания частиц и состояние псевдоожиженного слоя. Опытным путем установлено, что во многих случаях интенсивное перемешивание достигается уже при =2. Оптимальные значения устанавливаются обычно практически для каждого конктретного технологического режима и могут изменяться в довольно широких пределах.

При изменении скорости газа от нуля до слой остается неподвижным, порозность слоя и высота слоя остаются постоянными, перепад же давления интенсивно возрастает до значения , равного весу слоя с поперечным сечением 1 м .

, (4.56)

где и - плотность соответственно частиц и потока, кг /м .

Начало псевдоожижения наступает при равенстве силы гидравлического сопротивления слоя весу всех его частиц. Однако в действительности перепад давления в слое, соответствующий точке А, т.е. непосредственно перед началом псевдоожижения (т.В), несколько больше величины, необходимой для поддержания слоя во взвешенном состоянии. Это объясняется действием сил сцепления между частицами слоя, находящегося в покое. Когда скорость потока достигает значения , частицы преодолевают силы сцепления и перепад давлений становится равным весу частиц, приходящемуся на единицу площади поперечного сечения аппарата.

Рисунок 4.9 - Зависимость сопротивления слоя, порозности и насыпной плотности от скорости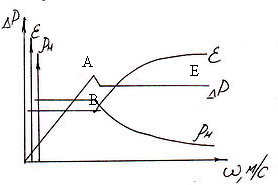

И з рисунка 4.9 видно, что указанное условие выполняется для всей области существования псевдоожиженного слоя (ВЕ линия) вплоть до того момента, когда скорость достигает величины, при которой слой разрушается и начинается массовый унос частиц потоком. Эту скорость называют скоростью уноса, или, иначе, скоростью свободного витания частиц и обозначают . Последнее название обусловлено тем, что при массовом уносе порозность слоя столь велика ( ), что движение отдельных частиц можно считать не зависящим от воздействия других частиц слоя. Каждая отдельная частица свободно витает, т.е. не осаждается и не уносится потоком, при условии, что ее вес в среде уравновешивается силой сопротивления, возникающей при обтекании частиц потоком. Значение можно найти, исходя из этого условия. Малейшее превышение скорости над величиной приводит к уносу частицы.

Пределы существования псевдоожиженного слоя ограничены критической скоростью или скоростью псевдложижения и скоростью витания , т.е. .

. (4.57)

Для неподвижного слоя высота и порозность остаются неизменными.

При увеличении скорости, как уже было отмечено, слой расшияется, высота его и порозность увеличиваются, а перепад давления остается неизменным и равным весу слоя. При неизменном весе слоя высота его увеличивается пропорционально отношению , а насыпная плотность слоя уменьшается в той же пропорции от , соответствующего насыпной плотности неподвижного слоя, до .

Зная вес слоя 1 м поперечного сечения , кг/м и приравняв его потери напора при движении потока через слой, можно определить критическую скорость псевдоожиженного слоя

. (4.58)

После преобразования получим уравнение для определения критической скорости псевдоожижения

, (4.59)

где - число Рейнольдса, соответствующее скорости ;

- критерий Архимеда.

При беспорядочной засыпке слоя можно в среднем принять , тогда уравнение (4.59) получит следующее выражение, позволяющее определить с точностью 20%:

. (4.60)

Для определения скорости витания частиц рекомендуется следующее уравнение:

. (4.61)

Таким образом, для слоя, состоящего из частиц одинакового диаметра , взвешенный слой может существовать при скорости потока , находящейся в пределах . Сопоставляя уравнения (4.60) и (4.61), получим

. (4.62)

Для очень мелких частиц при малых числах ; для крунпных частиц при больших числах .

4.5.5 Структура псевдоожиженного слоя

В промышленных условиях псевдоожиженный слой обычно состоит из частиц различных размеров. Это объясняется трудностью изготовления частиц строго одинакового размера, истиранием их в процессе работы. Практика эксплуатации установок каталитического крекинга показала, что фракция катализатора должна быть широкой и содержать некоторое минимальное количество мелких частиц, способствующих псевдоожижению и предохраняющих более крупные частицы от истирания (мелкие частицы изолируют крупные частицы друг от друга).

Различие в размерах частиц, входящих в состав полидисперсного слоя, оказывает влияние на порозность слоя, режим псевдоожижения, однородность слоя. Такой слой может иметь меньшую порозность благодаря более плотной упаковке частиц и возможности размещения мелких частиц в каналах между крупными частицами. При псевдоожижении полидисперсного слоя скорость потока может оказаться недостаточной для взвешивания крупных частиц и значительно превысить скорость витания мелких, которые при этом выносятся из слоя. В этом случае важным является диапазон изменения размеров частиц, измеряемый отношением .

Гидродинамические расчеты с использованием уравнений (5.25-5.27) для полидисперсного слоя затрудняются выбором расчетного диаметра частиц, учитывающего различие формы и размеров частиц и гранулометрический состав слоя. Наибольшую точность в расчетах можно получить, если эквивалентный расчетный диаметр частицы полидисперсного слоя определять экспериментально.

Приближенно диаметр частиц слоя модно определить в зависимости от способа выражения состава по выражениям

, (4.63)

, (4.64)

где и - соответственно объемная и массовая доля частиц диаметром в слое.

Эквивалентный диаметр паровых каналов полидисперсного слоя определяется как

(4.65)

либо . (4.66)

Вследствие полидисперсности слоя и стремления иметь повышенную скорость движения газа в аппарате, что позволяет иметь меньший его диаметр и более интенсивное псевдоожижение слоя, при осуществлении различных технологических процессов частицы обычно выносятся из слоя потоком газа. При выборе гидродинамического режима работы аппарата этот вынос частиц из слоя необходимо учитывать. В большинстве случаев желательно, чтобы вынос частиц был минимальным, т.к. это облегчает работу пылеулавливающих устройств.

Для количественного определения величины уноса частиц газом рекомендуется следующая формула:

, (4.67)

где - относительное количество частиц, унесенных потоком газа, % масс. на газ;

- скорость газа в свободном сечении аппарата, м/сек;

- массовая концентрация в слое мелких частиц, скорость витания которых равна или меньше ;

- высота слоя, мм;

- среднемассовый диаметр мелких частиц в слое, мкм;

- высота сепарационного пространства (расстояние от уровня слоя до сечения ввода газа в циклоны), мм;

- доля площади отверстий распределительной решетки; в существующих конструкциях эта величина обычно составляет 0,01-0,06;

- поправочный коэффициент, учитывающий физические свойства системы газ – твердое тело.

Численные значения величины А и n зависят от высоты сепарационного устройства.

Уравнение (4.67) получено на основании экспериментальных данных с использованием системы воздух - естественный алюмосиликатный катализатор; для перехода к другим системам служит коэффициент , который определяется из приближенного уравнения

, (4.68)

где - скорость витания частиц естественного алюмосиликатного катализатора, имеющего плотность 2080 кг/м ; в потоке воздуха при t=20°С и Р=0,1 МПа;

- скорость витания частиц того же диаметра данного материала в потоке газа в рабочих условиях.

При движении потока газа или жидкости через слой зернистого материала можно выделить основные типы структур псевдоожиженного слоя:

О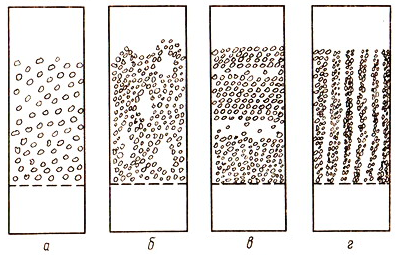 днородная структура (рисунок 4.10,а) практически возможна лишь при псевдоожижении твердых частиц в потоке капельной жидкости. Увеличение скорости сверх приводит к соответствующему возрастанию высоты слоя без каких-либо заметных колебаний его верхней границы. Расстояние между частицами в данном случае увеличивается постепенно, а жидкость движется в свободном объеме между ними сплошным потоком.

а -однородная; б-с барботажем пузырей; в-с поршнеобразованием; г-с каналообразованием

Рисунок 4.10 - Типы структур псевдоожиженного слоя

Однако в промышленности чаще используют псевдоожижение в системе газ – твердая фаза. Для этой системы псевдоожижение, как правило, является неоднородным: часть газа движется через слой не сплошным потоком, в виде пузырей, которые разрушаются, достигнув верхней границы слоя, что вызывает колебания высоты слоя (рисунок 4.10,б).

При увеличении скорости пузыри газа могут увеличиваться, достигая размера диаметра аппарата. Это так называемый поршневой режим псевдоожижения, явление нежелательное, т.к. при этом резко ухудшается равномерность контакта между газом и твердыми частицами (рисунок 4.10,в).

При псевдоожижении некоторых материалов однородность слоя нарушается вследствие каналообразования, при котором происходит проскок значительной части газа (жидкости) через один или несколько каналов, образующихся в слое (рисунок 4.10,г). Часто каналообразование наблюдается при применении материалов с очень мелкими или слипающимися частицами. Предельным случаем каналообразования является фнтанирование, при котором поток газа (или жидкости) прорывается через слой по одному большому каналу, возникающему близ оси аппарата.

4.5.6 Режим пневмотранспорта

Если скорость движения потока газа превышает скорость витания частиц, то последние начинают двигаться в направлении движения потока и система достигает режима пневмотранспорта. Скорость движения частиц при пневмотранспорте меньше скорости движения транспортирующего потока , который как бы скользит относительно движущейся частицы с относительной скоростью

. (4.69)

Как показали работы Тодеса, Горошко и Розенбаума, для режима вертикального пневмотранспорта в общем случае может быть использована зависимость, полученная для кипящего слоя, при условии, что число Рейнольдса определяется по относительной скорости скольжения ,т.е.

, (4.70)

где .

Важнейшим показателем пневмотранспорта является коэффициент взвеси m, равный отношению веса транспортируемых частиц к весу транспортирующего агента , т.е. равный числу килограммов частиц, поднимаемых 1 кг транспортирующего агента. С увеличением m сокращается расход транспортирующего агента, уменьшаются скорости движения потока и частиц, но увеличивается потеря напора в связи с ростом концентрации частиц в потоке.

При расчете пневмотранспорта приходится иметь дело с величиной подачи , равной отношению объемов частиц и транспортирующего агента .

Очевидно, что

, (4.71)

где и - плотность частиц и транспортирующего агента.

В величину общей потери напора при пневмотранспорте на высоту Н в общем случае входят следующие величины:

- статический напор, равный весу столба твердых частиц и транспортирующего агента:

, Па. (4.72)

При использовании в качестве транспортирующего агента газов или паров сравнительно невысокого давления величина обычно несоизмеримо мала по сравнению с , поэтому без заметной погрешности принимают

, Па. (4.73)

- потеря напора на трение транспортирующего агента о стенки пневмоствола

, Па, (4.74)

где - коэффициент гидравлического сопротивления;

- внутренний диаметр пневмоствола, м;

- приведенная длина пневмоствола, включающая местные сопротивления.

- потеря напора на трение транспортируемых частиц о стенки пневмоствола

, Па, (4.75)

где - коэффициент трения транспортируемых частиц о стенки пневмоствола.

- потеря напора на разгон транспортируемого материала

, Па, (4.76)

где - количество транспортируемого материала.

Таким образом

, Па. (4.77)

Во многих случаях основную часть сопротивления составляет .

Рассмотрим случай, когда гранулированный материал перемещается из аппарата с более низким давлением в аппарат с более высоким давлением . Высота стояка Н в этом случае должна быть такой, чтобы вес столба материала в стояке превышал разность давлений в аппаратах и сопротивление трения при движении материала в стояке , т.е.

, м, (4.78)

где - коэффициент запаса =1,2-1,3;

- плотность потока, кг/м .

Сопротивление определяется из уравнения

, Па. (4.79)

Сопротивлением трения паров о стенки можно пренебречь.