Раздел 3 теория физического и математического моделирования процессов химической технологии

3.1 Основы теории подобия

Теория подобия является учением о методах научного обобщения эксперимента. Она указывает, как надо ставить опыты и как обрабатывать их результаты, чтобы при проведении небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Применение теории подобия часто позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера; кроме того, опыты можно проводить не с рабочими (часто вредными и опасными) веществами и не в жестких (высокие температуры, агрессивные среды) условиях реального производственного процесса, а с другими (модельными) веществами в условиях, отличающихся от промышленных.

Проведение опытов на моделях, по меткому выражению Бэкеланда, позволяет делать ошибки в малом масштабе, а выгоды получать в большом.

Итак, методы теории подобия лежат в основе моделирования. Один из основных принципов теории подобия заключается в выделении из класса явлений группы подобных явлений. Например, такие разные на первый взгляд явления, как движение окружающего нас атмосферного воздуха и движение капельной жидкости по трубопроводу в основе своей однородны, так как по существу представляют собой перемещение вязкой жидкости под действием разности давлений; поэтому данные явления описываются едиными уравнениями Навье-Стокса и принадлежат к одному классу.

Подобным называется явления, для которых отношения характеризующих их сходственных величин постоянны.

3.2 Геометрическое, временное и физическое подобие. Инварианты и критерии подобия

Любой химико-технологический процесс протекает в определенном геометрическом контуре. Поэтому прежде всего устанавливают геометрическое подобие, временное, а затем подобие физическое, характеризующее данный процесс.

Две системы подобны геометрически, если отношения сходственных величин постоянны.

Простейший пример – подобие треугольников, сходственные линейные размеры которых параллельны, а отношения этих размеров постоянны. Подобные фигуры отличаются друг от друга только масштабом и могут быть получены одна из другой умножением сходственных размеров одной из них на некоторый постоянный масштабный множитель.

Безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных систем, называются константами подобия.

Пример: ,

где - размеры сторон одного треугольника;

- размеры сходственных сторон другого треугольника, подобного первому;

- константа геометрического подобия.

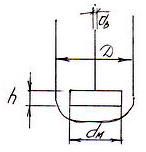
Геометрическое подобие удобнее выражать, вводя определенный геометрический размер. Так, если в рассматриваемой модели аппарата с мешалкой за определяющий размер принять диаметр лопасти мешалки и с ним сравнивать в данной модели все основные размеры,

; ; ; (3.1)

то геометрическое подобие будет соблюдаться, если в любом другом аппарате при той же определяющей характеристике сохраняется одинаковое значение размерных отношений, т.е.

; ; . (3.2)

Безразмерные отношения , сохраняющие одно и то же значение в модели и натуре, называются инвариантами геометрического подобия.

Рисунок 3.1 - Модель аппарата с мешалкой

Таким образом, геометрическое подобие будет соблюдаться тогда, когда инварианты геометрического подобия в сравнимых системах сохраняют одно и тоже значение, т.е. ; ; .

Безразмерность инвариантов подобия позволяет переносить условия геометрического подобия на аппараты любых размеров, важно лишь, чтобы отношение данного размера к определяющему следовало равенству (3.2). За определяющий размер может быть принят эквивалентный диаметр.

Инварианты геометрического подобия, выраженные в относительных величинах, называются также симплексами геометрического подобия, и означаются буквой Г.

При моделировании процессов, связанных с изменением свойств системы во времени, должно соблюдаться временное подобие.

Временное подобие предполагает, что частицы, находящиеся в сходственных точках и двигающиеся по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, находящиеся в постоянном соотношении.

. (3.3)

Системы, подобные во времени, будут и геометрически подобными; поэтому для таких систем соблюдается подобие полей скоростей ( ), температур ( ), концентраций (С) и других физических величин, т.е.

; ; . (3.4)

Для двух сравниваемых подобных систем каждая константа подобия имеет постоянное значение.

По аналогии с геометричесим и временным подобием физическое подобие соблюдается, когда его инварианты в сравнимых системах сохраняют одно и то же значение.

Инварианты физического подобия являются величинами безразмерными. Безразмерные инварианты физического подобия включают физические величины, имеющие разную размерность, носят название критериев подобия.

3.3 Методы получения критериев подобия

Физическое явление характеризуется рядом физических величин, имеющих разную размерность (скорость, плотность, вязкость и т.п.). Поэтому составление из этих величин безразмерных комплексов представляет основную задачу метода подобия.

Решение этой задачи осуществляется двумя путями:

- при помощи подобного преобразования дифференциальных уравнений;

- при помощи анализа размерностей.

I Подобное преобразование дифференциальных уравнений.

В результате подобного преобразования дифференциальных уравнений последние заменяются критериальными уравнениями. В этом случае инварианты физического подобия называются критериями подобия.

Для подобного преобразования дифференциальных уравнений пользуются правилом:

Критерии подобия можно получить путем деления левой части дифференциального уравнения на правую (или наоборот) и последующим отбрасыванием знаков математических операторов.

Рассмотрим уравнения движения вязкой жидкости (уравнение Навье-Стокса) и сделаем подобное преобразование его.

Для одномерного установившегося движения относительно оси это уравнение запишется:

. (3.5)

При изменении длины грани уравнение (3.5) приводится к виду:

Общее правило подобного преобразования диффузных уравнений:

Безразмерные комплексы физических величин можно получить путем деления слагаемых правой части уравнения на левую, или наоборот, с последующим отбрасыванием знаков математических операторов.

. (3.6)

Уравнение (3.6) представляет математическую модель движущейся вязкой жидкости, обладающей силой инерции ( ) и движущейся под действием силы тяжести ( ), сил давления ( ) и сил трения ( ). В уравнении (3.6) силы отнесены к единице объема и действуют на длине .

Сопоставим все действующие с силой инерции. Отношение этих сил к силам инерции (или наоборот) должно привести к получению безразмерных отношений (критериев подобия).

. (3.7)

Критерий Фруда ( ) отражает влияние сил тяжести или собственного веса на движение жидкости, является мерой отношения силы инерции к силе тяжести.

Критерий Фруда имеет одно и то же значение, т.е.

. (3.8)

. (3.9)

При решении технических задач гидродинамики важно определить не абсолютное давление Р в системе, а разность давлений между какими-либо точками или сечениями потока. Поэтому обычно критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости и имеет вид

. (3.10)

В подобных потоках

. (3.11)

. (3.12)

Критерий Рейнольдса ( ) отражает влияние силы трения на движение жидкости.

В подобных потоках

. (3.13)

Таким образом, выполненное преобразование позволяет дифференциальное уравнение движения жидкости заменить уравнением, выраженным в критериях подобия, в виде функции

. (3.14)

Вид функциональной связи может быть установлен только опытным путем. Так как уравнение (3.14) связывает между собой различные критерии, которые характеризуют действие различных сил в жидкости, то оно может быть названо критериальным уравнением установившегося движения вязкой жидкости. Если движение неустановившееся, то изменение скорости жидкости со временем при данном определяющем линейном размере системы характеризуется критерием неутановившегося движения - критерием гомохронности

, (3.15)

который вводится в критериальное уравнение (3.14).

Таким образом, дифференциальное уравнение Навье-Стокса, описывающее в общем виде движение вязкой жидкости, может быть представлено критериальным уравнением вида

, (3.16)

которое называется обобщенным критериальным уравнением гидродинамики.

В последнем уравнении критерии Фруда ( ), Рейнольдса ( ) и гомохронности ( ) являются определяющими, так как составлены из величин, выражающих условие однозначности. Критерий Эйлера является искомой величиной (размеры трубопровода, свойства жидкости и т.д.), т.е. определяемым критерием, относительно которого и записывается уравнение (3.16)

. (3.17)

Критериальное уравнение обычно записывается в виде степенного выражения. С учетом геометрического симплекса

, (3.18)

где значения определяют опытным путем.

II Анализ размерностей

В основе метода анализа размерностей лежит -теорема Бэкингема, которая читается так:

общую функциональную зависимость, связывающую между собой n переменных величин при m основных единицах их измерений можно представить в виде зависимости между (m-n) безразмерными комплексами этих величин, а в случае подобия - между (n-m) критериями подобия.

В гидродинамике размерность физических величин можно выразить тремя основными единицами (масса, длина, время), т.е. m=3. Тогда функциональную зависимость, связывающую пять физических величин (n=5) можно представить в виде зависимости между двумя безразмерными комплексами.

, (3.19)

Метод анализа размерностей требует предварительного знания числа переменных, от которых зависит анализируемое явление, проведение большого объема экспериментов для определения числа переменных величин n. При этом, если не учесть хотя бы одну из n величин, существенно влияющую на исследуемый процесс, полученное расчетное уравнение будет неверным.

3.4 Подобие гидродинамических процессов

Как отмечалось ранее, для описания движения вязкой жидкости критериальное уравнение имеет вид

. (3.20)

Для установившегося движения жидкости критерий гомохронности может быть исключен из уравнения (3.20), тогда

. (3.21)

В практических расчетах определяющие критерии имеют различную значимость. Это является следствием неодинакового влияния сил, действующих в жидкости, на конкретный процесс. Например, при установившемся движении жидкости по горизонтальному трубопроводу из перечисленных выше определяющих критериев наибольшую роль играют и , так как основное значение в данном случае имеют инерционные силы и силы вязкостного трения, отношение которых входит в критерий , а характеризует размеры трубопровода. Критерий может быть исключен, поскольку движение установившееся, а критерием можно пренебречь вследствие малого значения силы тяжести по сравнению с силами инерции и трения. Тогда зависимость (3.20) можно записать

. (3.22)

Моделирование на основе приведенной зависимости является приближенным.

В ряде случаев при описании гидродинамики целесообразно использовать сочетания критериев подобия, так называемые производные или модифицированные критерии подобия, составленные из основных.

Например, при естественной конвекции, возникающей вследствие разности плотностей, обусловленной наличием температур в разных точках этой жидкости, трудно определить скорость движения конвективных потоков. Для исключения скорости из критерия Фруда, отражающего действие сил тяжести, берут соотношение критериев

. (3.23)

Полученный безразмерный комплекс величин является производным критерием и называется критерием Галилея

. (3.24)

Умножив критерий Галилея на отношение ( )/ (где и - плотность жидкости в разных точках), отражающих причину возникновения конвективных токов, можно получить критерий Архимеда

. (3.25)

В подобных системах, в которых процессы протекают при естественной конвекции под действием силы тяжести, необходимо соблюдение равенства критериев Галилея или Архимеда.

3.5 Общая схема процесса математического моделирования

1 Постановка задачи - определяет цель и путь решение проблемы.

2 Анализ теоретических основ объекта исследования (составление физической модели процесса) – изучение теоретических основ по публикациям. Если не удается сформулировать (подобрать) удовлетворительную теорию – разрабатывается гипотеза. Правильность теории и гипотезы должна подтвердиться экспериментально.

3 Составление математической модели – математическое описание, включающее дифференциальные и конечные уравнения, отображающие влияние параметров на процесс. Для этого используют:

- уравнение материального и энергетического баланса;

- уравнений термодинамического равновесия и химического равновесия;

- кинетические уравнения.

4 Алгоритмизация математической модели - выбор метода решения.

5 Параметрическая идентификация – возможность определения численного значения коэффициентов модели расчетным или экспериментальным методами.

6 Проверка адекватности - соответствие модели и исследуемого объекта (критерий Фишера).

7 Моделирование на ЭВМ позволяет изменять параметры процесса в интересующем диапазоне.

8 Анализ полученной информации.