5. Электрические явления на поверхностях

21. Механизмы образования двойного электрического слоя (ДЭС). Соотношения между электрическим потенциалом и поверхностным натяжением (вывод уравнений Липпмана). Электрокапиллярные кривые и определение параметров ДЭС.

Различают три возможных механизма образования двойного электрического слоя:

1. Двойной электрический слой образуется в результате перехода ионов или электронов из одной фазы в другую (поверхностная ионизация). Например, с поверхности металла в газовую фазу переходят электроны, создавая электронное облако со стороны газовой фазы.

2. Образование двойного электрического слоя происходит в результате адсорбции. Двойной электрический слой может образоваться при избирательной адсорбции в межфазном слое ионов электролитов, не входящих в состав веществ, образующих фазы, т. е. в результате адсорбции примесей.

3. Если вещества, составляющие фазы системы, не способны обмениваться зарядами, то двойной электрический слой может образоваться благодаря ориентированию полярных молекул сопряженных фаз в результате их взаимодействия. Из объединенных первого и второго начал термодинамики, а также полного дифференциала энергии Гиббса выводится первое уравнение Липпмана, связывающее электрический потенциал с поверхностным натяжением:

где 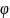и – электрический потенциал и избыточный заряд межфазной поверхности, соответственно.

Так как при записи этого уравнения использован метод избытков Гиббса, то все экстенсивные величины в нем являются избыточными. Полный дифференциал избытка внутренней энергии в этом случае равен:

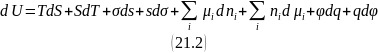
Вычтем из уравнения (21.1) уравнение (21.2):

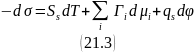
где 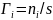– гиббсовская адсорбция. Нижний индекс s в этом уравнении указывает на отнесение к единице поверхности.

При условиях

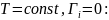
Первое уравнение Липмана

Из уравнения следует, что при самопроизвольном образовании ДЭС 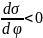, так как в этом случае заряд и потенциал имеют одинаковый знак, то есть формирование ДЭС ведет к снижению поверхностного натяжения, а в точке нулевого заряда 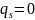поверхностное натяжение максимально .

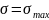ДЭС является конденсатором, поэтому емкость ДЭС можно определить как:

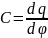
При подстановке этого уравнения в первое уравнение Липмана получим:

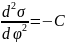
Второе уравнение Липмана

Выразим из этого соотношения заряд 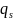и подставим его в первое уравнение Липпмана:

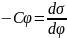
Рисунок 21.1 – Электрокапиллярная кривая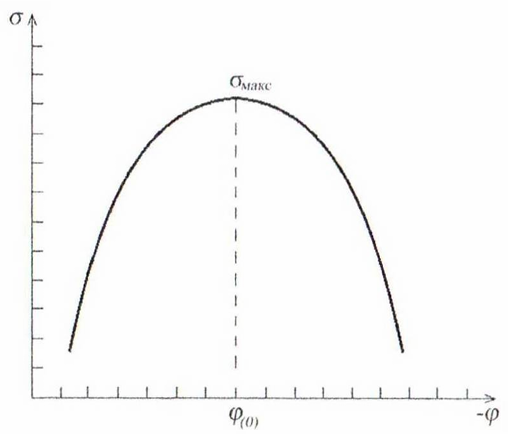

Э то уравнение показывает возможность определения емкости двойного электрического слоя, если известна зависимость от .

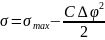
Это уравнение называют уравнением электрокапиллярной кривой. Из него следует, что поверхностное натяжение при условии постоянства емкости двойного электрического слоя изменяется в соответствии с уравнением параболы (рис. 21.1).

Вершина параболы отвечает максимальному поверхностному натяжению . Парабола симметрична, что по физическому смыслу означает равное сродство катионов и анионов, выступающих в роли противоионов, к поверхности, имеющей соответственно отрицательный и положительный потенциал. Уменьшение положительного потенциала, как и отрицательного, ведет к увеличению поверхностного натяжения. Однако в реальных системах емкость двойного электрического слоя несколько изменяется с изменением потенциала, и поэтому экспериментальные электрокапиллярные кривые обычно не являются симметричными. Вершина параболы соответствует точке нулевого заряда. В этой точке поверхностное натяжение не зависит от потенциала, так как производная равна нулю, т. е. поверхностный слой имеет нулевой заряд, что означает отсутствие двойного электрического слоя. Потенциал же поверхности в этой, точке не равен нулю.