4. Кинетические свойства дисперсных систем

18. Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия со блюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам.

Вывод уравнения

Рассмотрим, какие силы действуют на частицу при се свободной седиментации (оседании) со скоростью и под действием поля тяжести. Во-первых, это сила тяжести:

во-вторых, сила Архимеда:

и сила трения, возникающая при движении:

где – объем частицы, и – плотности частицы и дисперсионной среды соответственно, – коэффициент трения (так как рассматривается сферическая частица, ).

откуда:

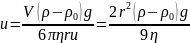
Условия применимости уравнения:

1. Частицы осаждаются независимо друг от друга (рассматриваются разбавленные системы).

2. Частицы имеют сферическую форму. Если частицы неправильной формы, вводится фактор формы.

3. Движение частиц происходит в ламинарном режиме ( ).

4. Размер частиц от 1 до 100 мкм, так как крупные частицы оседают ускоренно, мелкие начинают участвовать в броуновском движении.

5. В системе имеет место быть внутреннее (вязкое) трение.

С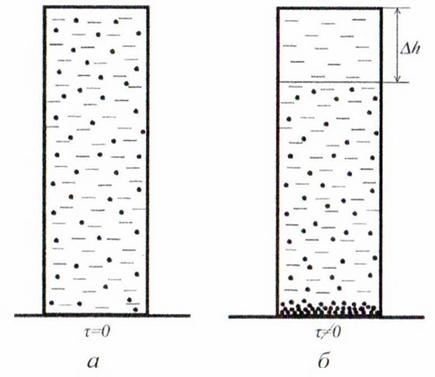 едиментационный анализ используется для определения размеров частиц в микрогетерогенных системах, содержащих частицы с размерами в интервале примерно от 1 до 100 мкм. В основе метода лежит определение скорости оседания частиц в жидкой среде с последующим расчетом их размеров по закону Стокса. При этом экспериментально с помощью чувствительных весов измеряют массу осевших частиц как функцию времени. Эта зависимость называется кривой седиментации.

Рисунок 18.1 – Седиментация частиц в монодисперсной системе в начальный (а) и некоторый (б) момент времени

Седиментационный анализ монодисперсной системы

Рассмотрим систему, где находится навеска массой . В момент времени единицу высоты столба суспензии приходится . Поскольку частицы одинаковые, они будут оседать с равной скоростью и будут проходить одинаковое расстояние , при том в осадок выпадут частицы общей массой

Кривая седиментации как функция в таком случае представляет собой прямую (рис. 18.2). Тангенс угла наклона этой прямой:

С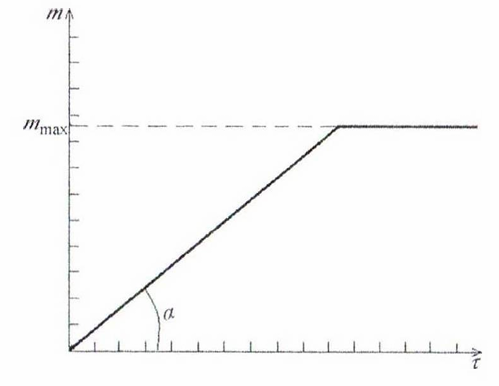 едиментационный анализ бидисперсной системы системы

Рисунок 18.2 – Седиментационная кривая монодисперсной системы

Рассмотрим систему с двумя навесками порошков массами и , содержащих монодисперсные частницы радиусами и соответственно, при том . При раздельной седиментации двух порошков получим две прямые и (рис. 18.3). К моменту времени полностью оседают частницы радиусом , а к моменту времени 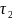– . Чтобы построить кривую седиментации строят прямую , параллельную прямой . Точка имеет ординату массы . Точка лежит на прямой , абцисса . Координаты точки . Ломанная – седиментационная кривая бидисперсной системы.

Седиментационный анализ полидиспер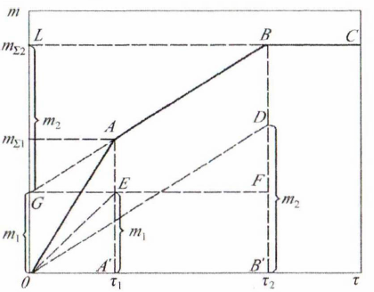 сной системы

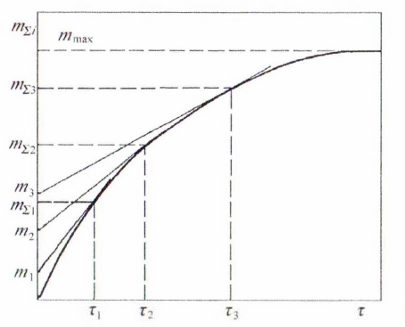
При рассмотрении полидисперсной системы (рис. 18.4) задача усложняется ввиду увеличения количества изломов (см. анализ бидисперсной системы).

Рисунок 18.4 – Седиментационная кривая полидисперсной системы

Д ля анализа применяются интегральные и дифференциальные кривые распределения массы частиц по радиусам.

Рисунок 18.3 – Седиментационная кривая бидисперсной системы

Интегральную кривую получают методом касательных (рис. 18.4). Проводят касательные к седиментационой кривой, которые пересекают ось ординат в точках масс осевших частиц одного радиуса. Для построения используют относительные массы :

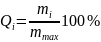
По полученным данным строят кривую распределения в координатах (рис. 18.5). Любая точка на этой кривой дает процентное содержание частиц с радиусами от максимального до данного. Отсюда следует, что представляет собой процентное содержание частиц с радиусами от до .

Дифференцирование интегральной кривой по радиусу дает дифференциальную кривую распределения массы частиц по радиусам. Радиус, который соответствует максимуму на этой кривой, называется наивероятнейшим радиусом (рис. 18.6).

Рисунок 18.5 – Интегральная кривая распределения массы частиц по радиусам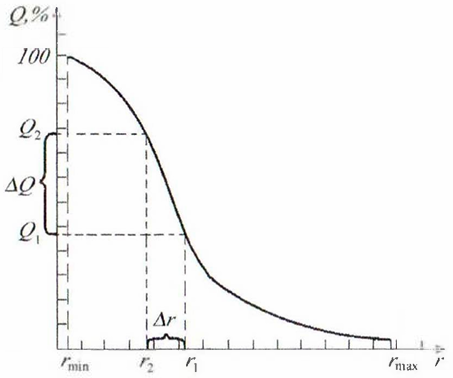

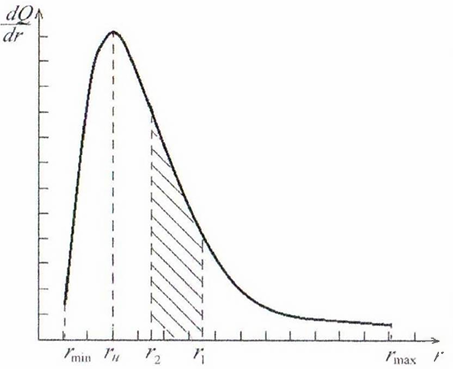
Рисунок 18.6 – Дифференциальнаяя кривая распределения массы частиц по радиусам

19. Природа броуновского движения. Понятие и определение среднеквадратичного сдвига по выбранному направлению. Взаимосвязь между среднеквадратичным сдвигом и коэффициентом диффузии (вывод закона Эйнштейна-Смолуховского). Экспериментальная проверка закона.

Природа броуновского движения. Частица, находящаяся в жидкости или газовой фазе, испытывает соударения со всех сторон с молекулами среды. Число этих соударений тем больше, чем крупнее частица. При большом числе соударений они компенсируют друг друга, и частица остается неподвижной. По мере уменьшения размеров частицы статистика начинает нарушаться, и частица начинает совершать сначала колебательные движения, а затем хаотично перемещаться – вовлекаться в броуновское движение.

Если исходить из предположения о тепловой природе броуновского движения, то для любой частицы, участвующей в этом движении, можно записать следующее соотношение

Поскольку тепловое движение частиц не является направленным вычислять скорость с высокой точность невозможно, средняя скорость движения частиц не может вы ступать в качестве основной характеристики теплового движения, поэтому используется значение среднеквадратичного сдвига

В общем случае частица движется в трехмерном пространстве:

Рассмотрим двумерное перемещение частицы:

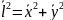
Тогда величина среднеквадратичного сдвига:

Закон Эйнштейна-Смолуховского связывает среднеквадратичный сдвиг с коэффициентом диффузии частицы.

Рассмотрим трубу с поперечным сечением , в которой частицы диффундируют вдоль оси под действием градиент концентрации. Мысленно рассечем трубу плоскостью перпендикулярно оси трубы (рис. 19.1). За тем слева и справа от этой плоскости выделим два равных участка трубы, величина которых по оси трубы равна среднеквадратичному сдви гу Δ за время . Среднюю частичную концентрацию золя (число частиц в единице объема золя) в выделенных участках (левом и правом) обо значим и соответственно. В силу сделанных предположений .

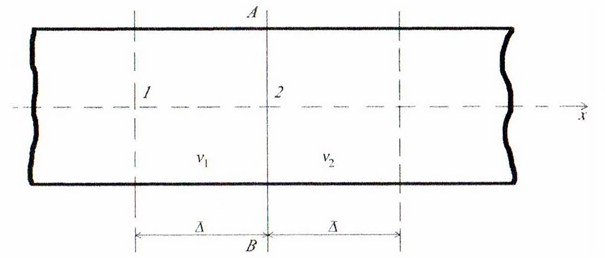
Рис. 19.1 – К выводу закона Эйнштейна-Смолуховского

Обозначим это число частиц слева и запишем соотношение:

Аналогичное соотношение можно записать для правого объема:

поэтому

Градиент концентраций:

По закону Фика:

Следовательно

Закон Эйнштейна-Смолуховского:

Справедливость закона Эйнштейна-Смолуховского для лиозолей была под­тверждена Сведбергом (1909 г.). С помощью ультрамикроскопа он измерял средний сдвиг частиц золя золота в зависимости от времени и вязкости среды. Зеддиг (1908 г.) подтвердил связь среднего сдвига частиц с температурой, вытекающую из закона Эйнштейна-Смолуховского. Перрен (1910 г.) использовал соотношение для определения числа Авогадро при исследовании броуновского движения коллоидных частиц гуммигута в воде и получил хорошее совпадение с величинами, полученными ра­нее другими методами. Это были первые экспериментальные определения числа Авогадро.

20. Седиментационно-диффузионное равновесие. Вывод уравнения (гипсометрический за кон Лапласа). Мера седиментационной устойчивости. Факторы, влияющие на седиментационную устойчивость дисперсных систем.

Рассмотрим систему, которая занимает промежуточное получение между золями и суспензиями и находится в равновесии, так как их частицы оседают в дисперсионной среде, но уже начинают участвовать в броуновском движении. На эти частицы действуют силы диффузии:

Седиментационный поток:

В зависимости от размера частиц и разности плотностей возможны три случая.

• При можно пренебречь диффузией, частицы оседают.

• При можно пренебречь седиментацией, частицы диффундируют.

• При частицы статичны, устанавливается седиментационно-диффузионное развонесие.

При установлении седиментационно-диффузионного равновесия можно приравнять правые части уравнений, полученных выше.

где и – частичная концентрация на нулевой высоте и высоте .

Гипсометрический закон Лапласа:

Мерой кинетической седиментационной устойчивости (КСУ) является величина, обратная константе седиментации:

Мерой термодинамической седиментационной устойчивости (ТСУ) является гипсометрическая высота. Ее удобнее определить как высоту , на протяжении которой концентрация дисперсной фазы изменяется в е раз:

Факторы, влияющие на седиментационную устойчивость дисперсной системы:

1. Размер частиц.

2. Вязкость дисперсионной среды.

3. Температура дисперсионной среды.