
- •Предмет и объекты коллоидной химии
- •Основы термодинамики и поверхностных явлений
- •Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (вывод уравнения Жюрена).
- •Адсорбционные равновесия
- •Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри. Основ ныеположения теории Ленгмюра, вывод уравнения и его анализ. Линейная форма уравнения Ленгмюра.
- •Теория полимолекулярной адсорбции бэт: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения бэт. Определение удельной поверхности адсорбентов, катализаторов и др.
- •Потенциальная теория адсорбции Поляни. Адсорбционный потенциал. Характеристическая кривая адсорбции. Температурная инвариантность и аффинность характеристических кривых.
- •Кинетические свойства дисперсных систем
- •Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия со блюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам.
- •Электрические явления на поверхностях
- •Общие представления о теориях строения дэс. Уравнение Пуассона-Больцмана для диффузной части дэс и его решение для случая слабозаряженных поверхностей. Уравнение Гуи Чепмена.
- •Современная теория строения дэс (теория Штерна); роль специфической адсорбции, перезарядка поверхности. Примеры образования дэс. Строение мицеллы (формулы дэс). Электрокинетические явления.
- •Агрегативная устойчивость и коагуляция дисперсных систем
- •Лиофильные дисперсные системы. Классификация и общая характеристика пав. Термодинамика и механизм мицеллообразования. Строение мицелл пав в водных и углеводородных средах. Солюбилизация.
- •Лиофильные дисперсные системы. Истинно растворимые и коллоидные пав, их классификация. Мицеллообразование, строение мицелл; методы определения ккм. Факторы, влияющие на ккм ионных и неионных пав.
- •Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, условия его применимости.
- •Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной структурой. Ползучесть, предел текучести.
Теория полимолекулярной адсорбции бэт: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения бэт. Определение удельной поверхности адсорбентов, катализаторов и др.
Теория полимолекулярной адсорбции была создана Брунауэром, Эмметом и Теллером и получила название по первым буквам фамилий создателей – БЭТ. В основе этой теории лежат те же исходные положения, что и в теории Ленгмюра, за исключением одного положения.
Рисунок
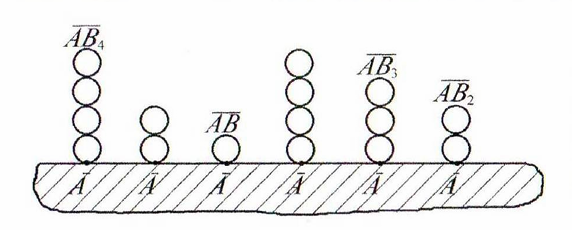
10.1 – Формирование полимолекулярного
слоя на поверхности адсорбента

 оложения
теории:
оложения
теории:
Адсорбция молекул адсорбата идет на адсорбционных центрах адсорбента. Все центры адсорбции идентичны друг другу, то есть поверхность адсорбента является энергетически однородной (эквипотенциальной).

Рисунок 10.2 – Изотерма полимолекулярной адсорбции
Каждая адсорбированная молекула является центром адсорбции для последующей молекулы, что ведет к формированию полимолекулярного слоя (рис. 10.1).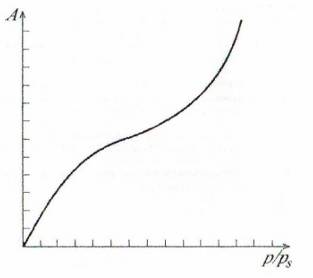
Адсорбированные молекулы не перемещаются по поверхности адсорбента (локализованная адсорбция).
Адсорбированные молекулы между собой не взаимодействуют или, иначе, латеральные взаимодействия в адсорбционном слое отсутствуют.
Рассмотрим полимолекулярную адсорбцию в виде ряда последовательных квазихимических реакций:

Обозначим константу равновесия первой реакции (для первого слоя) буквой К, второй – буквой К1, третьей – буквой К2. Затем запишем выражения для этих констант равновесия, следуя закону действия масс:

Из представленных уравнений получаются следующие выражения для концентрации соответствующих комплексов на поверхности адсорбента:

Авторы теории БЭТ приняли, что во всех слоях, кроме первого, взаимодействуют между собой в основном молекулы адсорбата, как и при конденсации. Поэтому было принято, что:

где
– константа конденсации пара, равная
отношению активностей вещества в жидком
состоянии
 и в состоянии насыщенного пара
и в состоянии насыщенного пара
 ,
принято
,
принято
 (стандартное состояние), а
(стандартное состояние), а

Для упрощения вывода и вида конечного уравнения поли молекулярной адсорбции введем обозначения:

Постоянная
 равна отношению констант равновесия
адсорбции (мономолекулярной) и конденсации
пара. Логарифмирование этого отношения
приводит к разности логарифмов констант,
а из этого следует, что постоянная
характеризует разность энергий Гиббса
процессов адсорбции и конденсации, т.
е. энергию Гиббса чистой адсорбции:
равна отношению констант равновесия
адсорбции (мономолекулярной) и конденсации
пара. Логарифмирование этого отношения
приводит к разности логарифмов констант,
а из этого следует, что постоянная
характеризует разность энергий Гиббса
процессов адсорбции и конденсации, т.
е. энергию Гиббса чистой адсорбции:

Учитывая уравнения (10.4) и (10.5), получим из уравнения (10.3):




Общее число активных центров на адсорбенте, или емкость монослоя, будет равна

Ряд в круглых скобках
 является геометрической прогрессией,
сумма членов которой равна
является геометрической прогрессией,
сумма членов которой равна
 при условии
при условии
 .
Поэтому:
.
Поэтому:

Величина адсорбции компонента
 равна:
равна:

Ряд
 является
производной по х предыдущей геометрической
прогрессии, и сумма ее членов равна
является
производной по х предыдущей геометрической
прогрессии, и сумма ее членов равна
 Поэтому:
Поэтому:

В качестве последнего шага следует
подставить значение
 ,
из уравнения (10.6) в уравнение (10.5) с учетом
того, что
,
из уравнения (10.6) в уравнение (10.5) с учетом
того, что
 получим уравнение изотермы
полимолекулярной адсорбции БЭТ:
получим уравнение изотермы
полимолекулярной адсорбции БЭТ:

Теорию БЭТ называют обобщенной теорией
Ленгмюра, поскольку в области низких
давлений, то есть при
 ,
уравнение БЭТ (10.8) трансформируется в
уравнение изотермы мономолекулярной
адсорбции Ленгмюра:
,
уравнение БЭТ (10.8) трансформируется в
уравнение изотермы мономолекулярной
адсорбции Ленгмюра:

Которое при
 переходит в закон Генри.
переходит в закон Генри.
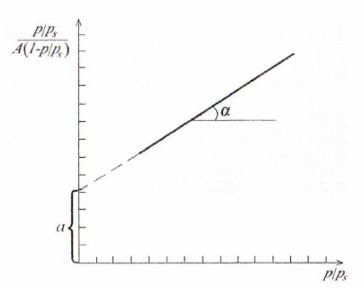
Константы уравнения БЭТ рассчитывают, используя его линейную форму:

Рисунок
10.3 – Изотерма полимолекулярной адсорбции
в координатах линейной формы уравнения
БЭТ
 ля
этого строят график в координатах
ля
этого строят график в координатах
 (рис. 10.3), из которого находят
и
(рис. 10.3), из которого находят
и
 ,
а затем из системы двух уравнений –
константы
,
и С:
,
а затем из системы двух уравнений –
константы
,
и С:


Полезно отмстить, что
 что облегчает расчет констант уравнения
БЭТ.
что облегчает расчет констант уравнения
БЭТ.
Константа имеет тот же физический смысл, что и в уравнении Ленгмюра и ее также используют для расчета удельной поверхности.
Если адсорбция измерена в молях на килограмм адсорбента, то по величине , можно рассчитать удельную поверхность адсорбента по следующему соотношению:
где – число Авогадро; – площадь, занимаемая молекулой адсорбата в плотном монослое.
В частности уравнение БЭТ, как правило,
соблюдается в интервале относительных
давлений
 .
При
.
При
 отклонения обусловлены наличием
энергетической неоднородности
поверхности, а при
отклонения обусловлены наличием
энергетической неоднородности
поверхности, а при
 начинают проявляться латеральные
взаимодействия в пределах одного
адсорбционного слоя. В этом заключается
внутреннее противоречие уравнения БЭТ
– оно учитывает взаимодействие молекул,
находящихся в соседних слоях, и нс
учитывает латеральные взаимодействия
в пределах одного слоя.
начинают проявляться латеральные
взаимодействия в пределах одного
адсорбционного слоя. В этом заключается
внутреннее противоречие уравнения БЭТ
– оно учитывает взаимодействие молекул,
находящихся в соседних слоях, и нс
учитывает латеральные взаимодействия
в пределах одного слоя.
Чтобы условия адсорбции при определении
удельной поверхности максимально
соответствовали теории БЭТ, используют
адсорбаты с малым межмолекулярным
взаимодействием – азот и благородные
газы. Как следствие, эти газы плохо
адсорбируются при комнатной температуре
на любых адсорбентах и при определении
удельной поверхности изотермы адсорбции
измеряют, проводя адсорбцию при
температуре кипения жидкого азота ( ).3
).3
Количественные характеристики пористых материалов: пористость, удельная поверхность, размер пор. Пористые тела корпускулярной, кристаллической и губчатой структуры, методы их получения. Классификация пор по Дубинину и теории физической адсорбции.
Пористые тела – это твердые тела, внутри которых имеются поры, обусловливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью.
Для адсорбентов удельную поверхность чаще рассчитывают по уравнению
и
выражают в
 .
Пористость
.
Пористость
 ,
как и удельная поверхность, может быть
рассчитана как отношение суммарного
объема пор
,
как и удельная поверхность, может быть
рассчитана как отношение суммарного
объема пор
 либо к объему пористого тела
:
либо к объему пористого тела
:

Либо к массе пористого тела
 :
:

где – плотность пористого материала.
Пористость часто выражают в процентах; она представляет собой долю объема пористого тела, которую занимают поры. Этот параметр важен для мембраны. В случае адсорбентов и катализаторов пористость чаще рассчитывают по последнему уравнению.
Для цилиндрических пор |
|
|
Для сферических пор |
|
|
Для щелевидных пор |
|
|
здесь
 – радиус пор;
– радиус пор;
 – высота пор;
– высота пор;
 –
длина пор,
–
длина пор,
 – ширина поры;
– число пор в единице массы или единице
объема пористого тела.
– ширина поры;
– число пор в единице массы или единице
объема пористого тела.
Таблица 11.1 – Классификация по Дубинину и теории физической адсорбции
Типы пор |
Размер пор |
Теории адсорбции |
Примеры |
Макропоры |
|
Теория Генри применима в области низких концентраций В области высоких концентраций применимы: - теория Ленгмюра для описания мономолекулярной адсорбции; - теория БЭТ для описания полимолекулярной адсорбции |
Катализаторы, адсорбенты |
Мезопоры |
|
Теория капиллярной конденсации |
Силикагели, алюмогели |
Микропоры |
|
Теория объемного заполнения пор |
Цеолиты |
Таблица 11.2 – Структуры тел
Типы структур |
Строение |
Методы получения |
Примеры |
Корпускулярная |
Состоит из отдельных частиц (корпускул), которые могут быть аморфными или слабоупорядоченными. Частицы не образуют чёткой кристаллической решётки. Характерна высокая пористость и развитая поверхность. |
Синтез гидрозоля
Для получения крупных пор используют пены. |
Адсорбенты и катализаторы: аэросилы (коллоидный диоксид кремния), цеолиты. |
Кристаллическая |
Чёткая периодическая решётка с упорядоченным расположением атомов или молекул. Может быть монокристаллической или поликристаллической. |
Медленная кристаллизация из расплавов или растворов. Гидротермальный синтез. Химическое осаждение из газовой фазы |
Алмаз, графит. Кварц (SiO₂). Металлы (медь, алюминий). Цеолиы. |
Губчатая |
Высокопористая, с хаотично расположенными порами и перегородками. Напоминает природную губку. Обладает большой удельной поверхностью. |
Обработка крупнопористых материалов в агрессивных средах. |
Губчатый никель (катализатор), пеностекло, углеродные пены, активные угли |
Адсорбция на пористых адсорбентах. Теория капиллярной конденсации. Капиллярно-конденсационный гистерезис. Расчет и назначение интегральной и дифференциальной кривых распределения объема пор по их размерам.
Пористые тела — это твердые тела, внутри которых имеются поры, обусловливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью.
Пористость – отношение суммарного объема пор к объему тела.

Для монодисперсных пор удельная поверхность

Таблица 12.1 – Типы пористых тел
Типы пор |
Размер пор |
Теории адсорбции |
Примеры |
Макропоры |
|
Теория Генри применима в области низких концентраций В области высоких концентраций применимы: - теория Ленгмюра для описания мономолекулярной адсорбции; - теория БЭТ для описания полимолекулярной адсорбции |
Катализаторы, адсорбенты |
Мезопоры |
|
Теория капиллярной конденсации |
Силикагели, алюмогели |
Микропоры |
|
Теория объемного заполнения пор |
Цеолиты |
Теория капиллярной конденсации используется для описания адсорбции на мезопористых адсорбентах. Основные положения:
Размеры пор Ø
 ,
удельная поверхность
,
удельная поверхность
 .
.Полимолекулярная адсорбция.
Краевой угол
 (происходит смачивание, образуются
вогнутые поры).
(происходит смачивание, образуются
вогнутые поры).
Абсорбция описывается уравнением
Кельвина ( – кривизна поверхности):
– кривизна поверхности):


-

(12.1)
Таблица 12.2 – Типы пор и абсорбция на них
Типы пор
Критерии сравнения |
Конические поры |
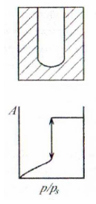
Цилиндрические тупиковые поры |
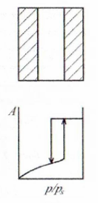
Цилиндрические открытые поры |
Изображение поры и изотерма адсорбции |
|
|
|
Кривизна графика |
Радиус поры не постоянен (
|
Радиус поры постоянен (
|
Адсорбция сначала происходит на
стенках, затем формируются вогнутые
цилиндрические мениски (выглядит как
двояковогнутая линза). Постепенно
радиус мениска уменьшается
После завершения адсорбции образуются сферические мениски, поэтому при десорбции происходит при меньшем давлении |
Наличие гистерезиса |
Гистерезиса нет, так как и адсорбция и десорбция описываются уравнение Кельвина (12.1), но только в случае, если нет дополни тельных осложняющих эффектов типа гистерезиса краевого угла |
Гистерезиса нет, так как и адсорбция и десорбция описываются уравнение Кельвина (12.1), но только в случае, если нет дополни тельных осложняющих эффектов типа гистерезиса краевого угла |
Гистерезис есть, так как адсорбция описывается уравнением
(кривизна цилиндрическая) Десорбция описывается уравнением Кельвина (12.1) |
Петля гистерезиса позволяет рассчитать интегральную и дифференциальную кривые распределения объема пор по их радиусам. Для расчета используют изотерму десорбции, так как только при десорбции можно предполагать, что во всех порах образуется сферический мениск и для расчета радиуса пор, независимо от их формы, можно использовать уравнение Кельвина (12.1).
И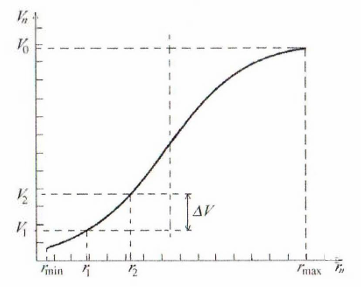 спользуют
равновесные давления в том диапазоне,
в котором наблюдается капиллярная
конденсация (в пределах петли гистерезиса).
Объем пор может быть рассчитан по
уравнению
спользуют
равновесные давления в том диапазоне,
в котором наблюдается капиллярная
конденсация (в пределах петли гистерезиса).
Объем пор может быть рассчитан по
уравнению

где
 – молярный объем жидкого адсорбата.
– молярный объем жидкого адсорбата.
В результате получают зависимость вида
 (рис. 12.1).
(рис. 12.1).
Рисунок
12.1 – Интегральная кривая распределения
объема пор по радиусам
Р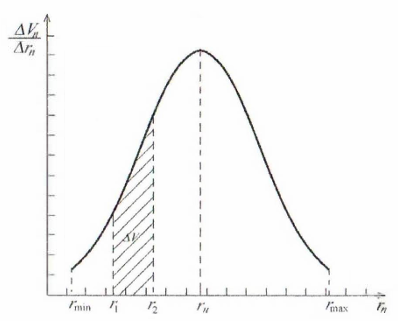 адиус,
соответствующий максимуму на
дифференциальной кривой, называют
наивероятнейшим радиусом, так как пор
с таким радиусом в адсорбенте больше
всего (их вклад в суммарный объем пор
максимален).
адиус,
соответствующий максимуму на
дифференциальной кривой, называют
наивероятнейшим радиусом, так как пор
с таким радиусом в адсорбенте больше
всего (их вклад в суммарный объем пор
максимален).
Рисунок
12.2 – Дифференциальная кривая распределения
объема пор по радиусам













 коагуляция для получения геля
высушивание и прокаливание геля.
коагуляция для получения геля
высушивание и прокаливание геля.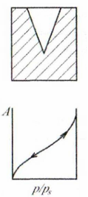
 ),
с ростом радиуса поры и, соответственно,
мениска
),
с ростом радиуса поры и, соответственно,
мениска
 уменьшается
кривизна
уменьшается
кривизна
 ,
давление увеличивается
,
давление увеличивается

 ),
следовательно радиус мениска постоянен
(
),
следовательно радиус мениска постоянен
( ),
давление постоянно
),
давление постоянно

 ,
повышение давления для прохождения
конденсации не требуется.
,
повышение давления для прохождения
конденсации не требуется.