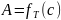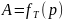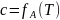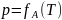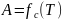- •Предмет и объекты коллоидной химии
- •Основы термодинамики и поверхностных явлений
- •Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (вывод уравнения Жюрена).
- •Адсорбционные равновесия
- •Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри. Основ ныеположения теории Ленгмюра, вывод уравнения и его анализ. Линейная форма уравнения Ленгмюра.
- •Теория полимолекулярной адсорбции бэт: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения бэт. Определение удельной поверхности адсорбентов, катализаторов и др.
- •Потенциальная теория адсорбции Поляни. Адсорбционный потенциал. Характеристическая кривая адсорбции. Температурная инвариантность и аффинность характеристических кривых.
- •Кинетические свойства дисперсных систем
- •Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия со блюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам.
- •Электрические явления на поверхностях
- •Общие представления о теориях строения дэс. Уравнение Пуассона-Больцмана для диффузной части дэс и его решение для случая слабозаряженных поверхностей. Уравнение Гуи Чепмена.
- •Современная теория строения дэс (теория Штерна); роль специфической адсорбции, перезарядка поверхности. Примеры образования дэс. Строение мицеллы (формулы дэс). Электрокинетические явления.
- •Агрегативная устойчивость и коагуляция дисперсных систем
- •Лиофильные дисперсные системы. Классификация и общая характеристика пав. Термодинамика и механизм мицеллообразования. Строение мицелл пав в водных и углеводородных средах. Солюбилизация.
- •Лиофильные дисперсные системы. Истинно растворимые и коллоидные пав, их классификация. Мицеллообразование, строение мицелл; методы определения ккм. Факторы, влияющие на ккм ионных и неионных пав.
- •Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, условия его применимости.
- •Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной структурой. Ползучесть, предел текучести.
Адсорбционные равновесия
Классификация механизмов адсорбции. Природа адсорбционных сил и их особенности при физической адсорбции. Вывод уравнения для энергии дисперсионного взаимодействия атома адсорбата с адсорбентом. Изотерма, изостера, изопикна адсорбции.
Процессы адсорбции классифицируют в соответствии с типом взаимодействия адсорбата с адсорбентом. Физико-химическая классификация основывается на том положении, что перераспределение компонентов между объемной фазой и поверхностным слоем может происходить под действием физических сил или в результате химической реакции между адсорбатом и адсорбентом.
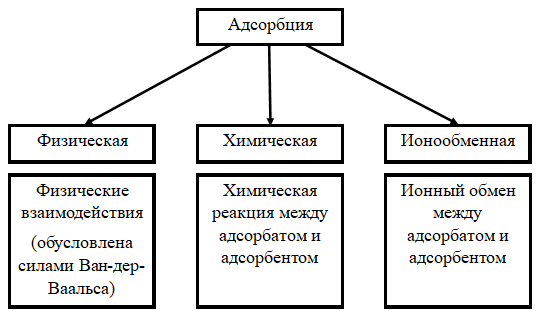
Рассмотрим подробнее физические взаимодействия. Различают три вида этих взаимодействий:
Ориентационное взаимодействие (силы Кеезома) обусловлено взаимодействием постоянных диполей и наблюдается при взаимодействии полярных молекул.
Индукционное взаимодействие (силы Дебая) наблюдается при взаимодействии полярной молекулы с неполярной. В этом случае постоянный диполь полярной молекулы своим полем наводит (индуцирует) диполь в неполярной молекуле и, в итоге, взаимодействуют постоянный и наведенный диполи.
Дисперсионное взаимодействие (силы Лондона) обусловлено взаимодействием мгновенных диполей. Флуктуация электронной плотности, происходящая постоянно и в любых молекулах, приводит к возникновению мгновенных диполей. Эти мгновенные диполи индуцируют мгновенные диполи в соседних молекулах. В чистом виде этот вид взаимодействия реализуется только при взаимодействии неполярных молекул.
Рисунок
8.1 – К выводу уравнения для энергии
притяжения атома

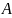 адсорбата к поверхности адсорбента
адсорбата к поверхности адсорбента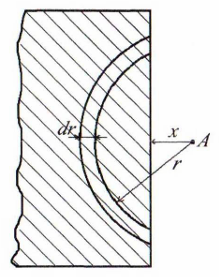 Вывод
уравнения для энергии дисперсионного
взаимодействия атома адсорбата с
адсорбентом
Вывод
уравнения для энергии дисперсионного
взаимодействия атома адсорбата с
адсорбентом
Для вывода уравнения воспользуемся
схемой, приведенной на рис. 8.1. На ней
представлен атом адсорбата
.
 – расстояние от
до поверхности адсорбента. Адсорбент
полубесконечный.
– расстояние от атома
до выделенного шарового сегмента.
Выделим шаровой слой толщиной
– расстояние от
до поверхности адсорбента. Адсорбент
полубесконечный.
– расстояние от атома
до выделенного шарового сегмента.
Выделим шаровой слой толщиной
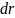 .
.
Рассчитаем энергию притяжения атома
адсорбата к атомам шарового слоя, умножив
энергию взаимодействия двух атомов на
число атомов в шаровом слое
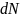 :
:
|
|
Число атомов в шаровом слое выразим
через число атомов в единице объема
адсорбента
и объем шарового слоя
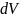 :
:

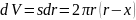
Подставим в уравнение (8.1) полученные уравнения:
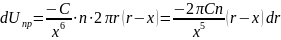
Проинтегрируем в пределах от минимального до максимального расстояния от атома адсорбата до поверхности адсорбента:

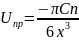
Вклад дисперсионных сил приводит к тому, что энергия притяжения становится дальнодействующей. Таким образом, уравнение для полной энергии взаимодействия принимает вид:

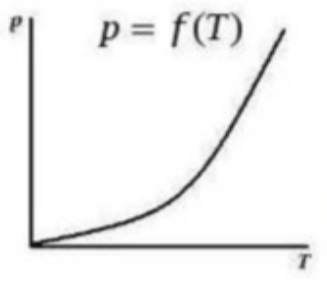
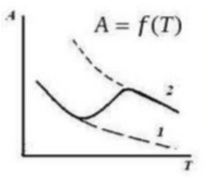
Таблица 8.1 – Изотерма, изостера, изопикна адсорбции
Изотерма |
Изостера |
Изопикна |
|
|
|
|
|
|
Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри. Основ ныеположения теории Ленгмюра, вывод уравнения и его анализ. Линейная форма уравнения Ленгмюра.
Поверхность твердых тел, как правило,
неоднородна геометрически (шероховатость,
наличие дефектов) и химически, и чтобы
получить простейшие закономерности
адсорбции, необходимо предположить,
что поверхность адсорбента однородна
и распределение адсорбата происходит
в мономолекулярном слое. Если поверхностный
слой представить как отдельную фазу,
то можно рассматривать процесс
перераспределения вещества как
выравнивание химических потенциалов
распределяемого вещества в адсорбционном
слое
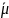 и в объеме
и в объеме
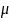 до
до
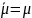 .
.
Используя определение термодинамической активности:
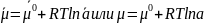
При условии равновесия:

где
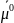 и
– химический потенциал распределяемого
вещества в адсорбционном слое и в объеме
в стандартных состояниях соответственно;
и
– химический потенциал распределяемого
вещества в адсорбционном слое и в объеме
в стандартных состояниях соответственно;
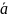 и
и
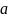 – активности распределяемого вещества
в адсорбционном слое и объеме
соответственно;
– активности распределяемого вещества
в адсорбционном слое и объеме
соответственно;
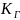 – константа распределения, называемая
константой Генри; она не зависит
от концентрации.
– константа распределения, называемая
константой Генри; она не зависит
от концентрации.
Для неэлектролитов (в том числе для
газов, паров)
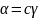 и тогда:
и тогда:
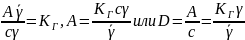
где
– величина адсорбции – концентрация
адсорбата в адсорбционном слое или
количество вещества в адсорбционном
слое, приходящееся на единицу поверхности
(на единицу массы адсорбента); с –
концентрация в объеме;
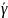 и
– коэффициент активности адсорбата в
адсорбционном слое и объеме соответственно;
и
– коэффициент активности адсорбата в
адсорбционном слое и объеме соответственно;
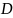 – коэффициент распределения.
– коэффициент распределения.
Уравнения в общем виде отражают изотерму адсорбции при любых концентрациях. Однако коэффициенты активности, как и величина адсорбции, зависят от концентрации, а вид зависимости чаще всего неизвестен.
Т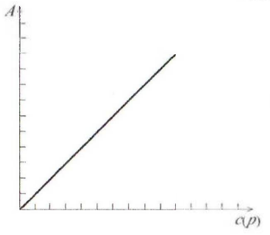 ак
как для бесконечно разбавленных растворов
(при малом давлении газов, паров)
коэффициенты активности равны единице,
то на основании последнего уравнения
можно сформулировать следующую
закономерность: при разбавлении системы
(уменьшение давления) коэффициент
распределения стремится к постоянному
значению, равному константе распределения
Генри. В этом и состоит закон Генри.
Относительно величины адсорбции А
этот закон запишется так:
ак
как для бесконечно разбавленных растворов
(при малом давлении газов, паров)
коэффициенты активности равны единице,
то на основании последнего уравнения
можно сформулировать следующую
закономерность: при разбавлении системы
(уменьшение давления) коэффициент
распределения стремится к постоянному
значению, равному константе распределения
Генри. В этом и состоит закон Генри.
Относительно величины адсорбции А
этот закон запишется так:
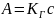

Рисунок
9.1 – Изотерма адсорбции в координатах
уравнения Генри
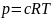 ,
т. е.
,
т. е.
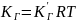 .
.
Эти уравнения представляют собой изотермы адсорбции вещества при малых концентрациях. В соответствии с ними закон Генри можно сформулировать так: величина адсорбции при малых давлениях газа (концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации). При адсорбции на твердых адсорбентах область действия этого закона мала из-за неоднородности поверхности.
Вывод уравнения изотермы Ленгмюра базируется на ряде исходных положений, которые и составляют основу модели (теории) Ленгмюра.
Адсорбция молекул адсорбата идет на адсорбционных центрах адсорбента. Все центры адсорбции идентичны друг другу, то есть поверхность адсорбента является энергетически однородной (эквипотенциальной).
На каждом адсорбционном центре адсорбируется только одна молекула, что означает мономолекулярную адсорбцию.
Адсорбированные молекулы не перемещаются по поверхности адсорбента (локализованная адсорбция).
Адсорбированные молекулы между собой не взаимодействуют или, иначе, латеральные взаимодействия в адсорбционном слое отсутствуют.
Воспользуемся термодинамическим подходом и рассмотрим элементарный акт адсорбции, как обратимую квазихимическую реакцию:
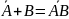
где
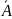 – адсорбционный центр;
– адсорбционный центр;
 – молекула адсорбата;
– молекула адсорбата;
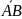 – адсорбционный комплекс. Запишем
уравнение для константы адсорбционного
равновесия К в соответствии с законом
действия масс (без учета коэффициентов
активности):
– адсорбционный комплекс. Запишем
уравнение для константы адсорбционного
равновесия К в соответствии с законом
действия масс (без учета коэффициентов
активности):

Перейдем к другим обозначениям
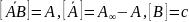
где
А – адсорбция (абсолютная), равная числу
молей адсорбата в адсорбционном слое,
отнесенному к единице поверхности или
единице массы адсорбента, и равная
количеству занятых адсорбционных
центров;
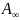 – емкость адсорбционного монослоя или
общее количество (число молей) адсорбционных
центров, отнесенное к единице поверхности
или единице массы адсорбента.
– емкость адсорбционного монослоя или
общее количество (число молей) адсорбционных
центров, отнесенное к единице поверхности
или единице массы адсорбента.
С учетом новых обозначений:

Выразим величину адсорбции и получим уравнение изотермы мономолекулярной адсорбции Ленгмюра
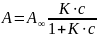
Рисунок
9.2 – Изотерма мономолекулярной адсорбции
Ленгмюра
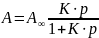
Отношение
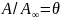 носит название степени заполнения
поверхности. Его часто вводят в уравнение
Ленгмюра:
носит название степени заполнения
поверхности. Его часто вводят в уравнение
Ленгмюра:
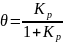

Рассмотрим два предельных случая.
Сначала рассмотрим область низких
давлений (или низких концентраций). В
этой области
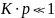 ,
,
 ,
а уравнение Ленгмюра трансформируется
в закон Генри:
,
а уравнение Ленгмюра трансформируется
в закон Генри:
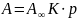
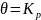
При этом
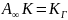 .
Отсюда следует, что закон Генри является
частным случаем уравнения Ленгмюра, а
начальный участок изотермы адсорбции
действительно должен быть линейным.
.
Отсюда следует, что закон Генри является
частным случаем уравнения Ленгмюра, а
начальный участок изотермы адсорбции
действительно должен быть линейным.
В области больших давлений (больших
концентраций)
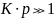 ,
,
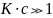 .
В этом случае уравнения переходят в
следующие простые соотношения:
.
В этом случае уравнения переходят в
следующие простые соотношения:
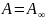
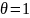
Полученный результат означает, что адсорбция достигла своего предельного значения, и вся поверхность адсорбента покрыта мономолекулярным слоем адсорбированных молекул. Поэтому величину называют емкостью мономолекулярного слоя.
Если адсорбция измерена в молях на килограмм адсорбента, то по величине , можно рассчитать удельную поверхность адсорбента по следующему соотношению:
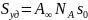
где
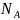 – число Авогадро;
– число Авогадро;
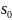 – площадь, занимаемая молекулой адсорбата
в плотном монослое.
– площадь, занимаемая молекулой адсорбата
в плотном монослое.
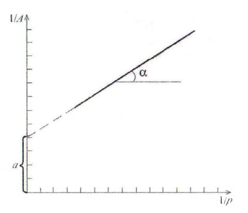
Рисунок
9.3 – Изотерма адсорбции в координатах
линейной формы уравнения Ленгмюра
 ля
расчета констант уравнения Ленгмюра
используется линейная форма этого
уравнения. Чтобы его получить, нужно
единицу поделить на левую и правую части
уравнений
ля
расчета констант уравнения Ленгмюра
используется линейная форма этого
уравнения. Чтобы его получить, нужно
единицу поделить на левую и правую части
уравнений
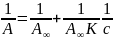
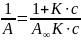
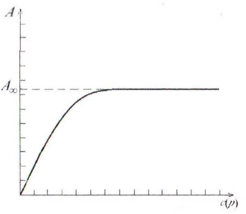
Из последнего соотношения следует, что
изотерма мономолекулярной адсорбции,
построенная в координатах
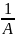 -
-
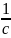 ,
должна представлять собой прямую (см.
рис. 9.3), если уравнение Ленгмюра описывает
полученные данные. Из сопоставления
уравнения и рис. 9.3 следует, что отрезок,
отсекаемый на оси ординат при экстраполяции
прямой, равен
,
должна представлять собой прямую (см.
рис. 9.3), если уравнение Ленгмюра описывает
полученные данные. Из сопоставления
уравнения и рис. 9.3 следует, что отрезок,
отсекаемый на оси ординат при экстраполяции
прямой, равен
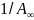 , а тангенс угла наклона прямой равен
величине
, а тангенс угла наклона прямой равен
величине
 .
.
В итоге получаем систему двух уравнений, из которых можно легко найти , и .
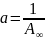
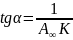
Следует отмстить, что иногда используется
несколько иная линейная форма уравнения
Ленгмюра. Чтобы ее получить, нужно левую
и правую части уравнения умножить на
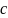 :
:

Теперь график нужно строить в координатах
 ,
а система уравнений для расчета констант
будет выглядеть следующим образом:
,
а система уравнений для расчета констант
будет выглядеть следующим образом:
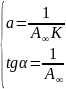
Мономолекулярная адсорбция в основном наблюдается при адсорбции газов, находящихся при температуре выше критической, и адсорбции из растворов. При адсорбции паров, как правило, адсорбция не завершается образованием монослоя, а идет дальше, то есть формируется полимолекулярный слой.


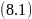
 Изотерма
адсорбции в координатах уравнения
Генри
Изотерма
адсорбции в координатах уравнения
Генри