- •Предмет и объекты коллоидной химии
- •Основы термодинамики и поверхностных явлений
- •Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (вывод уравнения Жюрена).
- •Адсорбционные равновесия
- •Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри. Основ ныеположения теории Ленгмюра, вывод уравнения и его анализ. Линейная форма уравнения Ленгмюра.
- •Теория полимолекулярной адсорбции бэт: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения бэт. Определение удельной поверхности адсорбентов, катализаторов и др.
- •Потенциальная теория адсорбции Поляни. Адсорбционный потенциал. Характеристическая кривая адсорбции. Температурная инвариантность и аффинность характеристических кривых.
- •Кинетические свойства дисперсных систем
- •Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия со блюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам.
- •Электрические явления на поверхностях
- •Общие представления о теориях строения дэс. Уравнение Пуассона-Больцмана для диффузной части дэс и его решение для случая слабозаряженных поверхностей. Уравнение Гуи Чепмена.
- •Современная теория строения дэс (теория Штерна); роль специфической адсорбции, перезарядка поверхности. Примеры образования дэс. Строение мицеллы (формулы дэс). Электрокинетические явления.
- •Агрегативная устойчивость и коагуляция дисперсных систем
- •Лиофильные дисперсные системы. Классификация и общая характеристика пав. Термодинамика и механизм мицеллообразования. Строение мицелл пав в водных и углеводородных средах. Солюбилизация.
- •Лиофильные дисперсные системы. Истинно растворимые и коллоидные пав, их классификация. Мицеллообразование, строение мицелл; методы определения ккм. Факторы, влияющие на ккм ионных и неионных пав.
- •Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, условия его применимости.
- •Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной структурой. Ползучесть, предел текучести.
Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (вывод уравнения Жюрена).
Дисперсность (или удельная поверхность) является самостоятельным термодинамическим параметром состояния системы, изменение которого вызывает изменение других равновесных свойств системы. Такую зависимость можно объяснить увеличением с ростом дисперсности доли вещества, находящегося в поверхностном слое, т. е. в коллоидном состоянии. Происходит переход вещества из одного состояния в другое, или из одной модификации в другую.
Согласно правилу фаз Гиббса число параметров, определяющих состояние системы, равно

где
– число степеней свободы системы
(количество параметров, которые модно
изменить без изменения состояния
системы);
 – число компонентов в системе;
– число компонентов в системе;
 – число фаз;
– число фаз;
 – число факторов, влияющих на систему.
– число факторов, влияющих на систему.
Если пренебречь наличием межфазной
поверхности, из правила фаз Гиббса
следует, что для рассмотренной системы
при указанных условиях ( )
число степеней свободы равно единице
(
)
число степеней свободы равно единице
( ).
Это значит, что произвольно можно
изменять только количество ПАВ в системе,
остальные свойства при этом будут
принимать соответствующие значения.
При постоянном содержании ПАВ состояние
системы фиксировано, что соответствует
).
Это значит, что произвольно можно
изменять только количество ПАВ в системе,
остальные свойства при этом будут
принимать соответствующие значения.
При постоянном содержании ПАВ состояние
системы фиксировано, что соответствует
 .
Однако из приведенного примера
следует, что при увеличении удельной
поверхности распределение ПАВ в системе
изменяется, а это означает, что система
обладает дополнительной степенью
свободы. Таким образом, удельная
поверхность, или дисперсность, выступает
как интенсивный признак системы.
.
Однако из приведенного примера
следует, что при увеличении удельной
поверхности распределение ПАВ в системе
изменяется, а это означает, что система
обладает дополнительной степенью
свободы. Таким образом, удельная
поверхность, или дисперсность, выступает
как интенсивный признак системы.
Подводя итог, можно сделать вывод, что дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:
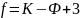
Рисунок
5.1 – К выводу уравнения Лапласа
 дним
из параметров, которыми характеризуют
дисперсность, является кривизна
поверхности:
дним
из параметров, которыми характеризуют
дисперсность, является кривизна
поверхности:

Возрастающая роль поверхностной энергии проявляется в появлении кривизны поверхности жидкости, уменьшающей площадь поверхности при данном объеме. Если жидкость находится на поверхности другого конденсированного тела, то при оценке кривизны следует учитывать и адгезию, которая, как и сила тяжести, способствует растеканию.
Кривизна вызывает изменение площади и
положения межфазной поверхности, что
можно выразить приращением поверхностной
энергии .
Кроме того, изменяются объемы фаз
.
Кроме того, изменяются объемы фаз
 и
и
 на
на
 и
и
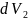 .
При условии постоянства объема всей
системы
.
При условии постоянства объема всей
системы
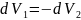 . Изменение объемов вызывает
соответствующие изменения энергий фаз
и
на
. Изменение объемов вызывает
соответствующие изменения энергий фаз
и
на
 и
и
 (где
(где
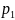 и
и
 – давления внутри фаз). Соотношение
между поверхностной энергией и «объемной»
можно записать с помощью обобщенного
уравнения первого и второго начал
термодинамики относительно энергии
Гельмгольца
при
– давления внутри фаз). Соотношение
между поверхностной энергией и «объемной»
можно записать с помощью обобщенного
уравнения первого и второго начал
термодинамики относительно энергии
Гельмгольца
при
 :
:

При равновесии между фазами
 ,
тогда:
,
тогда:

или, опуская индекс при ,
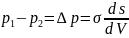
где
 характеризует кривизну поверхности;
характеризует кривизну поверхности;
 – разность давлений в фазах.
– разность давлений в фазах.
Из этого следует, что если фазы разделены
искривленной поверхностью, то условиям
равновесия будут отвечать разные
давления в этих фазах. При этом в фазе
с положительной кривизной поверхности
будет более высокое давление. Если
давление в фазе
будет поддерживаться постоянным и
равным, например, давлению атмосферы,
то величина
будет
характеризовать разность между давлением
в конденсированной фазе
с искривленной поверхностью
 ,
и давлением в фазе той же природы с
плоской поверхностью
,
и давлением в фазе той же природы с
плоской поверхностью
 то есть
то есть
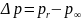 .
Величину
в этом случае называют капиллярным
давлением. Для тела со сферической
формой поверхности
.
Величину
в этом случае называют капиллярным
давлением. Для тела со сферической
формой поверхности
 и тогда уравнение принимает следующий
вид:
и тогда уравнение принимает следующий
вид:

В случае цилиндрической поверхности


Кривизну поверхности неправильной
формы характеризуют с помощью соотношения
 ,
а влияние кривизны на давление выразится
соотношением
,
а влияние кривизны на давление выразится
соотношением
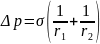
Уравнения, выражающие взаимосвязь между кривизной поверхности тела и изменением его внутреннего давления, носят название уравнений Лапласа. Из них, в частности, следует, что давление внутри жидкости с положительной кривизной больше давления внутри той же жидкости с плоской поверхностью. Изменения давления внутри жидкости, обусловленные кривизной ее поверхности, являются причиной разнообразных капиллярных явлений.
Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание).
Рисунок
5.2 – Поднятие (а) и опускание (б) жидкости
в капиллярах: а
– лиофильный капилляр; б – лиофобный
капилляр; в – взаимосвязь между радиусом
мениска

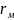 и радиусом капилляра
и радиусом капилляра

 первом капилляре (лиофильная поверхность
смачивается) (рис. 5.2, а) поверхность
жидкости имеет отрицательную кривизну,
поэтому дополнительное давление Лапласа
стремится растянуть жидкость (давление
направлено к центру кривизны) и поднимает
ее в капилляре.
первом капилляре (лиофильная поверхность
смачивается) (рис. 5.2, а) поверхность
жидкости имеет отрицательную кривизну,
поэтому дополнительное давление Лапласа
стремится растянуть жидкость (давление
направлено к центру кривизны) и поднимает
ее в капилляре.
Кривизна поверхности жидкости во втором капилляре (лиофобная поверхность, не смачивается) (рис. 5.2, б) положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:

где
 – плотность жидкости;
– плотность жидкости;
 – плотность газовой фазы;
– плотность газовой фазы;
 – ускорение свободного падения;
– ускорение свободного падения;
 – радиус мениска.
– радиус мениска.
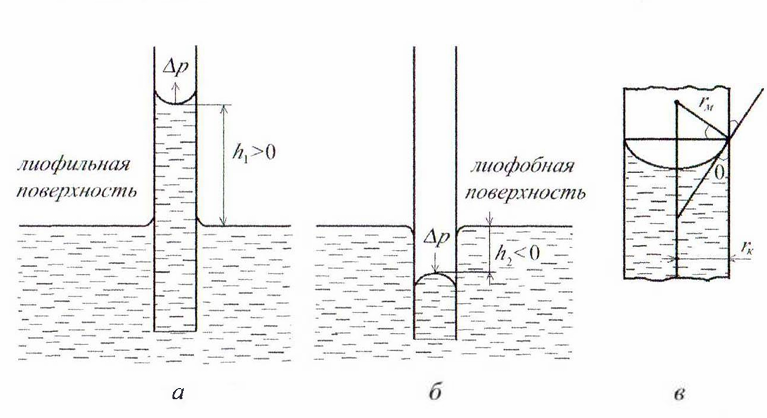
Чтобы высоту капиллярного поднятия
связать с характеристикой смачивания,
радиус мениска необходимо выразить
через угол смачивания
 и радиус капилляра
и радиус капилляра
 .
На рис. 5.2, (в) показан (в увеличенном
виде) мениск жидкости в капилляре. Видно,
что
.
На рис. 5.2, (в) показан (в увеличенном
виде) мениск жидкости в капилляре. Видно,
что
 ,
тогда высоту капиллярного поднятия
можно представить в виде формулы Жюрена:
,
тогда высоту капиллярного поднятия
можно представить в виде формулы Жюрена:

При отсутствии смачивания
 ,
уровень жидкости в капилляре опускается
на величину
,
уровень жидкости в капилляре опускается
на величину
 .
При полном смачивании
.
При полном смачивании
 ,
в этом случае радиус мениска равен
радиусу капилляра.
,
в этом случае радиус мениска равен
радиусу капилляра.
Влияние дисперсности на термодинамическую реакционную способность. Вывод уравнения капиллярной конденсации Кельвина и его анализ. Влияние дисперсности на растворимость, температуру фазового перехода и константу равновесия химической реакции.
Термодинамическая реакционная способность
указывает на удаленность данного
состояния вещества или системы компонентов
от равновесного состояния при определенных
условиях. Термодинамическая реакционная
способность определяется химическим
сродством, которое можно выразить
изменением энергии Гиббса поверхности
или разностью химических потенциалов.
Реакционная способность зависит от
степени дисперсности вещества, изменение
которой может приводить к сдвигу фазового
или химического равновесия. Соответствующее
приращение энергии Гиббса
 (благодаря изменению дисперсности)
можно представить в виде объединенного
уравнения первого и второго начал
термодинамики:
(благодаря изменению дисперсности)
можно представить в виде объединенного
уравнения первого и второго начал
термодинамики:
Влияние дисперсности на термодинамическую реакционную способность:
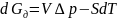
Для индивидуального вещества
 и при
имеем:
и при
имеем:

Уравнение Лапласа:

Подставим уравнение (6.1) в уравнение Лапласа и получим:

Для сферической кривизны:

Если рассматривается переход вещества из конденсированной фазы в газообразную, то энергию Гиббса можно выразить через давление пара, приняв его за идеальный. Дополнительное изменение энергии Гиббса, связанное с изменением дисперсности, составляет:

Объединяя уравнения (6.2) и (6.3), получим уравнение Кельвина (уравнение капиллярной конденсации):

где
 – насыщенное давление пара адсорбата,
– насыщенное давление пара адсорбата,
 – равновесное давление пара адсорбата.
– равновесное давление пара адсорбата.
Для неэлектролитов его можно записать следующим образом (влияние дисперсности на растворимость):

Из уравнения видно, что с увеличением
дисперсности растворимость растет, или
химический потенциал частиц дисперсной
системы больше, чем у крупной частицы,
на величину
 .
.
Влияние дисперсности на температуру фазового перехода:
Влияние дисперсности на равновесие химической реакции:

М



 етоды
получения дисперсных систем:
диспергирование и конденсация. Уравнение
Ребиндера для работы диспергирования.
Адсорбционное понижение прочности
(эффект Ребиндера). Конденсация физическая
и химическая. Энергия Гиббса образования
зародыша новой фазы при гомогенной
конденсации; роль пересыщения.
етоды
получения дисперсных систем:
диспергирование и конденсация. Уравнение
Ребиндера для работы диспергирования.
Адсорбционное понижение прочности
(эффект Ребиндера). Конденсация физическая
и химическая. Энергия Гиббса образования
зародыша новой фазы при гомогенной
конденсации; роль пересыщения.
Диспергирование и конденсация – методы получения свободнодисперсных систем: порошков, суспензий, золей, в том числе аэрозолей, эмульсий и т. д. Под диспергированием понимают дробление и измельчение вещества, под конденсацией – образование гетерогенной дисперсной системы из гомогенной в результате ассоциации молекул, атомов или ионов в агрегаты.
Рассмотрим диспергирование веществ в конденсированном состоянии. Чтобы разрушить твердое тело или жидкость и получить новую поверхность, необходимо преодолеть когезионные силы, или силы, обусловливающие целостность определенного объема твердого тела или жидкости. При диспергировании под действием внешних сил конденсированное вещество сначала претерпевает объемное деформирование (упругое и пластическое) и только после этого при определенном механическом усилии оно разрушается.
Работа упругого и пластического деформирования пропорциональна объему тела:
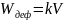
где
 – коэффициент пропорциональности,
равный работе объемного деформирования
единицы объема конденсированного тела;
– коэффициент пропорциональности,
равный работе объемного деформирования
единицы объема конденсированного тела;
 – объем тела.
– объем тела.
Работа образования новой поверхности при диспергировании пропорциональна приращению поверхности:

где
– энергия образования единицы поверхности,
или поверхностное натяжение;
 – приращение поверхности, или площадь
образовавшейся поверхности.
– приращение поверхности, или площадь
образовавшейся поверхности.
Полная работа, затрачиваемая на диспергирование, выражается уравнением Ребиндера:

Учтем, что объем тела пропорционален
линейному размеру в кубе
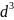 ,
а площадь поверхности пропорциональна
линейному размеру в квадрате
,
а площадь поверхности пропорциональна
линейному размеру в квадрате
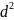 .
Тогда уравнение можно привести к
следующему виду
.
Тогда уравнение можно привести к
следующему виду

Используя последнее соотношение, можно рассмотреть два предельных случая:
При большой величине
 (большом размере тела)
(большом размере тела)
 и тогда общая работа диспергирования
становится равной работе деформирования:
и тогда общая работа диспергирования
становится равной работе деформирования:

В этом случае говорят о дроблении материала.
При малой величине (маленьком размере частиц)
 и тогда общая работа диспергирования
определяется затратами работы на
создание новой поверхности:
и тогда общая работа диспергирования
определяется затратами работы на
создание новой поверхности:

В этом случае используется термин «измельчение».
Особенностью диспергирования является то, что по мере диспергирования растет прочность материала. Дело в том, что разрушение идет по местам дефектов, а чем меньше размер, тем меньше дефектов и выше прочность.
Уменьшить работу диспергирования можно снижением величины σ, что достигается использованием ПАВ, которое можно подобрать для любой межфазной поверхности. Снижение прочности материалов (работы диспергирования) в результате адсорбции ПАВ составляет суть эффекта, называемого эффектом Ребиндера. Этот эффект нашел широкое применение при получении высокодисперсных порошков. Синтез частиц размером менее 100 нм проводится в основном методом конденсации.
Различают гомогенную и гетерогенную конденсацию:
Гомогенная конденсация протекает на центрах конденсации, которые образуются самопроизвольно в результате флуктуации плотности (концентрации).
Гомогенная конденсация возможна только
в системе, которая находится в пересыщенном
состоянии. При конденсации пара
пересыщение (или степень пересыщения)
 характеризуют отношением давления
пара в пересыщенной системе
характеризуют отношением давления
пара в пересыщенной системе
 к давлению пара в насыщенной системе
:
к давлению пара в насыщенной системе
:

При кристаллизации (образовании частиц) в растворе степень пересыщения раствора характеризуют аналогичным соотношением

где
 и
и
 – концентрация растворенного вещества
в пересыщенном и насыщенном растворах,
соответственно.
– концентрация растворенного вещества
в пересыщенном и насыщенном растворах,
соответственно.
В пересыщенном паре в результате флуктуации плотности самопроизвольно возникают центры конденсации (микрокапли), давление паров над которыми, в соответствии с уравнением Кельвина, будет больше, чем величина:

где – радиус центра конденсации (микрокапли).
Из этого уравнения следует, что при небольшой степени пересыщения:
может быть такое состояние, при котором
 ,
и тогда в такой пересыщенной системе
центры конденсации будут непрерывно
образовываться и испаряться. Такое
состояние системы называется
метастабильным. Система в этом состоянии
термодинамически неустойчива, но
кинетически устойчива. В отсутствие
посторонних центров конденсации степень
пересыщения в метастабильном состоянии
может быть достаточно большой.
,
и тогда в такой пересыщенной системе
центры конденсации будут непрерывно
образовываться и испаряться. Такое
состояние системы называется
метастабильным. Система в этом состоянии
термодинамически неустойчива, но
кинетически устойчива. В отсутствие
посторонних центров конденсации степень
пересыщения в метастабильном состоянии
может быть достаточно большой.
Началу образования новой фазы – возникновению центров конденсации – соответствует определенная критическая степень – пересыщения, зависящая как от природы веществ, так и от наличия ядер конденсации. В противном случае конденсация не может происходить, исчезают и зародыши конденсации (путем их испарения, растворения, плавления). При гомогенной конденсации происходит самопроизвольное образование зародышей; энергия поверхности выступает в качестве потенциального барьера конденсации. Энергию Гиббса образования зародышей выражают (в соответствии с объединенным уравнением первого и второго начал термодинамики) в виде четырех составляющих: энтропийной, механической, поверхностной и химической.
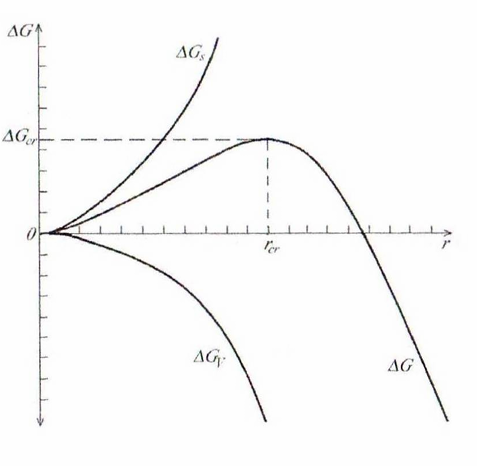 Поведение
зародышей конденсации в системах,
находящихся в метастабильном состоянии,
легко понять, рассматривая зависимость,
представленную на рис. и используя
уравнение
Поведение
зародышей конденсации в системах,
находящихся в метастабильном состоянии,
легко понять, рассматривая зависимость,
представленную на рис. и используя
уравнение

где
 – критическая степень пересыщения.
– критическая степень пересыщения.
Рисунок
7.1 – Зависимость энергии Гиббса
образования зародыша новой фазы от его
радиуса при


Если степень пересыщения больше критической величины, то возникающие зародыши будут самопроизвольно расти
Критическая энергия Гиббса образования
зародышей конденсации соответствует
критической точке – максимуму функции
 :
:

Гетерогенная конденсация протекает на посторонних центрах конденсации – частицах пыли, ионах, стенках сосуда и др.
Различают физические и химические методы конденсации.
Физическую конденсацию можно вызвать и понижением температуры, если это ведет к получению пересыщенной системы. Примером физической конденсации является приготовление дисперсий ртути кипячением ртути и отводом ее паров в раствор ПАВ в воде. После конденсации паров образуется стабилизированная дисперсия ртути в воде.
Химические методы конденсации
основаны на проведении какой-либо
химической реакции, которая сопровождается
образованием малорастворимого соединения.
Для синтеза золей металлов чаще всего
используется реакция восстановления
соответствующих ионов. Так получают
золи серебра, золота, никеля и др.
Химическая реакция может быть проведена
и в газовой фазе. Так получают, например,
высокодисперсный
 (аэросил), сжигая
(аэросил), сжигая
 .
.