
- •Предмет и объекты коллоидной химии
- •Основы термодинамики и поверхностных явлений
- •Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (вывод уравнения Жюрена).
- •Адсорбционные равновесия
- •Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри. Основ ныеположения теории Ленгмюра, вывод уравнения и его анализ. Линейная форма уравнения Ленгмюра.
- •Теория полимолекулярной адсорбции бэт: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения бэт. Определение удельной поверхности адсорбентов, катализаторов и др.
- •Потенциальная теория адсорбции Поляни. Адсорбционный потенциал. Характеристическая кривая адсорбции. Температурная инвариантность и аффинность характеристических кривых.
- •Кинетические свойства дисперсных систем
- •Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия со блюдения закона Стокса. Седиментационный анализ, расчет и назначение кривых распределения частиц по размерам.
- •Электрические явления на поверхностях
- •Общие представления о теориях строения дэс. Уравнение Пуассона-Больцмана для диффузной части дэс и его решение для случая слабозаряженных поверхностей. Уравнение Гуи Чепмена.
- •Современная теория строения дэс (теория Штерна); роль специфической адсорбции, перезарядка поверхности. Примеры образования дэс. Строение мицеллы (формулы дэс). Электрокинетические явления.
- •Агрегативная устойчивость и коагуляция дисперсных систем
- •Лиофильные дисперсные системы. Классификация и общая характеристика пав. Термодинамика и механизм мицеллообразования. Строение мицелл пав в водных и углеводородных средах. Солюбилизация.
- •Лиофильные дисперсные системы. Истинно растворимые и коллоидные пав, их классификация. Мицеллообразование, строение мицелл; методы определения ккм. Факторы, влияющие на ккм ионных и неионных пав.
- •Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, условия его применимости.
- •Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной структурой. Ползучесть, предел текучести.
Ньютоновские жидкости, уравнения Ньютона и Пуазейля. Методы измерения вязкости. Уравнение Эйнштейна для вязкости дисперсных систем, условия его применимости.
В зависимости от наличия или отсутствия предела текучести все дисперсные системы делят на твердообразные и жидкообразные . В свою очередь, жидкообразные системы делят на ньютоновские и неньютоновские системы.
К ньютоновским относятся системы,
течение которых подчиняется закону
Ньютона (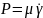 ).
Зависимость
).
Зависимость
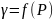 ,
называемую в общем случае кривой течения,
у ньютоновских жидкостей является
линейной; вязкость ньютоновских систем
не зависит от
и
.
К числу ньютоновских относятся многие
агрегативно устойчивые дисперсные
системы с невысокой концентрацией
дисперсной фазы.
,
называемую в общем случае кривой течения,
у ньютоновских жидкостей является
линейной; вязкость ньютоновских систем
не зависит от
и
.
К числу ньютоновских относятся многие
агрегативно устойчивые дисперсные
системы с невысокой концентрацией
дисперсной фазы.
Свойствами ньютоновской жидкости обладают многие агрегативно устойчивые дисперсные системы с относительно невысокой концентрацией частиц, форма которых не отличается большой асимметрией.
Взаимосвязь между вязкостью дисперсной
системы и значениями
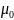 и
была получена Эйнштейном теоретически
для разбавленных дисперсных систем,
содержащих недеформируемые частицы и
в отсутствие взаимодействий между ними:
и
была получена Эйнштейном теоретически
для разбавленных дисперсных систем,
содержащих недеформируемые частицы и
в отсутствие взаимодействий между ними:
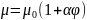
– объемная доля (объемная концентрация) дисперсной фазы;
– вязкость дисперсионной среды;
– коэффициент, величина которого зависит от формы частиц (для сферических частиц 2,5; для частиц неправильной формы он больше).
Методы измерения вязкости (кривых течения):
Капиллярные вискозиметры. Измерение вязкости базируется на использовании уравнения Гагена-Пуазсйля.
Приборы, работа которых базируется на использовании закона Стокса. Примером здесь являются вискозиметры с падающим шаром (вискозиметры Хепплера).

Рисунок 33.1 – Измерительная ячейка ротационного вискозиметра:
1 – внешний цилиндр; 2 – внутренний цилиндр; 3 – исследуемая система
Д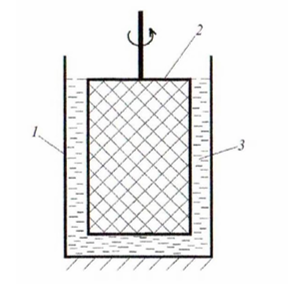 ля
более вязких систем и с целью измерения
кривых течения в достаточно большом
диапазоне напряжений и скоростей
сдвига используются ротационные
вискозиметры. В простейшем случае
измерительная ячейка такого вискозиметра
состоит из двух коаксиальных цилиндров,
вложенных друг в друга. Пространство
между стенками цилиндров заполняется
исследуемой системой. Внутренний
цилиндр (ротор) приводится во вращение
мотором, в результате чего система
подвергается деформации сдвига (рис.
33.1).
ля
более вязких систем и с целью измерения
кривых течения в достаточно большом
диапазоне напряжений и скоростей
сдвига используются ротационные
вискозиметры. В простейшем случае
измерительная ячейка такого вискозиметра
состоит из двух коаксиальных цилиндров,
вложенных друг в друга. Пространство
между стенками цилиндров заполняется
исследуемой системой. Внутренний
цилиндр (ротор) приводится во вращение
мотором, в результате чего система
подвергается деформации сдвига (рис.
33.1).
Реологический метод исследования структур в дисперсных системах. Реологические модели идеальных тел (модели Гука, Ньютона, Сен-Венана-Кулона). Кривые течения реальных жидкообразных и твердообразных структурированных систем.
Реологические свойства реальных тел моделируют с использованием моделей идеальных тел, каждая из которых демонстрирует одно из реологических свойств - упру гость, пластичность, вязкость.
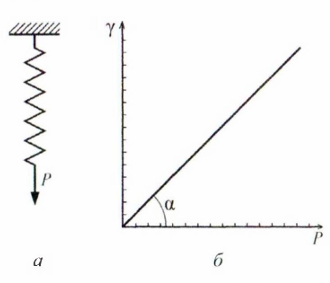
Рисунок 34.1 – Модель идеально упругого тела Гука (а) и зависимость его деформации от напряжения(б) |
Идеально упругое тело (модель Гука)
иллюстрируют идеально упругой пружиной,
деформация которой подчиняется закону
Гука:
Котангенс угла наклона прямой к оси
абсцисс равен модулю упругости (
|
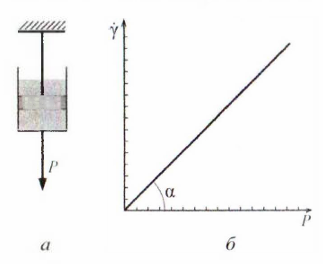
Рисунок 34.2 – Модель идеально вязкой жидкости Ньютона (а) и зависимость скорости его деформации от напряжения (б) |
Идеально вязкое тело Ньютона (модель Ньютона) принято представлять перфорированным поршнем, перемещающимся в цилиндре, заполненном идеально вязкой жидкостью (рис. 34.2, а). Течение идеально вязкой жидкости описывается законом Ньютона:
– вязкость (динамическая);
|
Рисунок 34.3 – Модель идеально пластичного тела Сен-Венана Кулона (а) и зависимость его деформации от напряжения (б) |
Идеально пластичное тело (модель
Сен-Венана-Кулона). Элемент сухого
трения, у которого сила трения не
зависит от скорости перемещения одного
тела по поверхности другого. Эта модель
может бесконечно деформироваться,
когда приложенное напряжение равно
или превышает силу трения, то есть
некоторое напряжение
|

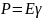 ,
– модуль упругости (рис. 34.1)
,
– модуль упругости (рис. 34.1)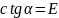 ).
).
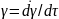 - скорость деформации (скорость
перемещения поршня в цилиндре);
– время деформации
- скорость деформации (скорость
перемещения поршня в цилиндре);
– время деформации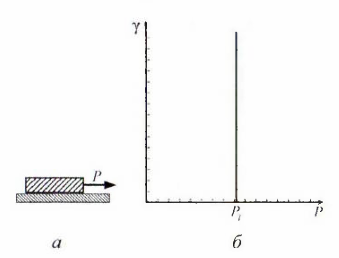
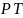 ,
называемое пределом текучести (рис.
34.3, б). При
,
называемое пределом текучести (рис.
34.3, б). При
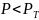 модель не деформируется, то сеть в
этих условиях
модель не деформируется, то сеть в
этих условиях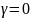 .
.