27. Лиофильные дисперсные системы. Истинно растворимые и коллоидные пав, их классификация. Мицеллообразование, строение мицелл; методы определения ккм. Факторы, влияющие на ккм ионных и неионных пав.

Для лиофильных дисперсных систем характерно хорошее взаимодействие между дисперсной фазой и дисперсионной средой (большая работа адгезии), что ведет к низкому значению межфазного натяжения и малой поверхностной энергии . Эти системы могут образовываться самопроизвольно за счет либо самопроизвольного диспергирования одной из фаз, либо за счет образования ассоциатов молекул при увеличении их концентрации в растворе (по аналогии с конденсацией). Лиофильные системы являются равновесными и термодинамически устойчивыми. У этих систем нет термодинамических причин для коагуляции.

Примеры: мицеллярные растворы ПАВ и растворы высокомолекулярных веществ (в определенных условиях).

Таблица 27.1 – Классификация ПАВ

По поведению в растворах
Истинно растворимые (до )	Коллоидные (больше )
Образуют гомогенные (истинные) растворы при любых концентрациях вплоть до предела растворимости	При их определенной концентрации в растворе образуют гетерогенные системы, которые относятся к числу лиофильных термодинамически устойчивых дисперсных систем (ассоциативные, или мицеллярные коллоиды), поэтому в дальнейшем будут рассматриваться только коллоидные ПАВ. Минимальная концентрация ПАВ, при которой осуществляется переход от истинного раствора к гетерогенной системе за счет образования мицелл (ассоциатов молекул ПАВ), называется критической концентрацией мицеллообразования (ККМ) и принимает обычно значения в интервале
По способности диссоциировать в растворах
Неионогенные	Ионогенные
Не диссоциируют в растворах. Примеры: оксиэтилированные спирты, кислоты, амины	Анионные – диссоциируют в водных растворах с образованием поверхностно-активного аниона. Катионные – при диссоциации в воде образуют поверхностно активные катионы. Амфотерные (амфолиты) – в зависимости от раствора они могут проявлять свойства анионного или катионного ПАВ

Рисунок 27.1 – Схематическое изображение прямых (а) и обратных (б) мицелл

М ицеллобразование. При добавлении коллоидного ПАВ в воду вначале образуется обычный гомогенный раствор, но при достижении ККМ наступает такое состояние, при котором гомогенная система трансформируется в гетерогенную за счет образования мицелл, то есть ассоциатов, состоящих из молекул ПАВ (или ионов в случае ионного ПАВ).

Ориентация молекул ПАВ в прямой мицелле такова, что углеводородные (гидрофобные) радикалы образуют неполярное ядро мицеллы («микрокаплю» углеводорода), находящееся в жидкокристаллическом состоянии. Полярные группы молекул (ионов) ПАВ обращены к водной фазе и экранируют неполярное ядро мицеллы от полярной дисперсионной среды. Такое строение мицеллы обеспечивает очень низкое межфазное натяжение на границе мицелла – раствор (сотые доли ) (рис. 27.1, а). В обратной мицелле ориентация молекул обратная в виду сродства углеводородных радикалов к растворителю (рис. 27.1, б).

Мицеллообразование протекает самопроизвольно так как структурообразование приводит к снижению энтропии, возрастающей при росте концентрации ПАВ.

Структура мицеллы:

*ПОИ и ПИ находятся в адсорбционном слое

Рисунок 27.1 – Зависимость мутности , удельной электропроводности 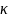и поверхностного натяжения раствора ионогенного ПАВ к от его концентрации

Методы определения ККМ

1. По зависимости удельной электропроводности раствора от концентрации ионогенных ПАВ (рис. 27.1, ).

2. По зависимости мутности раствора от концентрации ионогенных ПАВ (рис. 27.1, ).

3. По зависимости поверхностного натяжения раствора от концентрации ионогенных ПАВ (рис. 27.1, ).

4. По зависимости вязкости раствора от концентрации ионогенных ПАВ.

5. По зависимости оптической плотности раствора от концентрации ионогенных ПАВ.

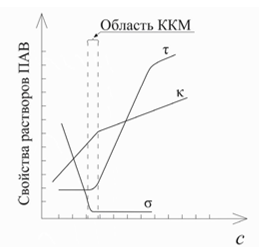
Факторы, влияющие на ККМ (всё следует из формулы):

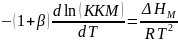
1. Температура. Характер влияния температуры на величину ККМ зависит от знака величины . Для водных мицеллярных растворов ионогенных ПАВ , тогда . C ростом температуры величина ККМ у этих ПАВ повышается. Повышение температуры растворов неионных ПАВ вызывает дегидратацию полярных (оксиэтиленовых) групп ( ), что ведет к снижению значений ККМ.

2. Длина углеводородного радикала в молекуле ПАВ. Удлинение углеводородного радикала сопровождается уменьшением величины ККМ для водных (полярных) растворов. Растворимость коллоидных ПАВ в неполярных растворителях увеличивается с ростом длины углеводородного радикала и это ведет к повышению значения ККМ. Способность к мицеллообразованию появляется только у молекул, углеводородный радикал которых содержит 8-10 групп 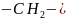. Количественная взаимосвязь между величиной ККМ и длиной радикала в форме:

	– в водных (полярных) растворах
	– в неполярных растворителях

где – число атомов углерода в алкильной цепи; и – константы для данного гомологического ряда ПАВ. Константа зависит от типа полярной группы и температуры; константа определяется энергией растворения, приходящейся на одну - - группу.

3. Тип и строение полярной группы. При равной длине углеводородного радикала значение ККМ у неионогенного ПАВ существенно меньше (на порядки), чем у ионогенного Растворимость диссоциирующих веществ обычно выше растворимости неэлектролитов из-за лучшей гидратации ионов. Также влияет отталкивание диссоциированных полярных групп при образовании мицелл. В неполярных средах с малой диэлектрической проницаемостью диссоциация практически отсутствует и различие между ионогенным и неионогенным ПАВ нивелируется.

4. Добавки электролитов. Введение в раствор сильного электролита оказывает высаливающее действие из-за конкуренции за молекулы растворителя. Растворимость того вещества, которое уже находилось в растворе до введения электролита, после его введения падает. Введение электролитов в раствор ПАВ будет снижать величину ККМ, ярко выражен в случае ионогенных ПАВ, так как в результате повышения ионной силы раствора у этого типа ПАВ снижается еще и степень диссоциации.

В растворах неполярных растворителей диссоциация слаба, не влияет на ККМ

Таблица 27.1 – Факторы, влияющие на ККМ

	Полярные растворители	Неполярные растворители
Длина углеводородного радикала
	Ионогенные	Неионогенные
Температура
Природа полярной группы
Введение электролита		Не влияет

28. Лиофобные дисперсные системы. Факторы агрегативной устойчивости лиофобных систем. Быстрая и медленная коагуляция. Кинетика коагуляции по Смолуховскому (вывод уравнения). Определение константы скорости и времени половинной коагуляции. Зависимость числа частиц разного порядка от времени.

К числу лиофобных относится большинство обычных дисперсных систем (золи, суспензии, эмульсии), приготовление которых требует затрат энергии на диспергирование или на создание пересыщенного состояния при конденсационном методе получения. Эти системы являются термодинамически неустойчивыми из-за плохой адгезии между дисперсной фазой и дисперсионной средой (из-за высоких значений и ).

Факторы агрегативной устойчивости. Стабилизации лиофобной дисперсной системы будет способствовать любой фактор, который снижает межфазное натяжение и создает потенциальный барьер, препятствующий коагуляции.

1. Электростатический (или ионно-сольватный) фактор действует при формировании на межфазной поверхности двойного электрического слоя. Образование ДЭС сопровождается снижением межфазного натяжения (см. первое уравнение Липпмана) и появлением сил отталкивания между частицами электростатической природы

2. Адсорбционно-сольватный фактор. Сольватация поверхности способствует адгезии между дисперсной фазой и дисперсионной средой и может привести к формированию структурированного поверхностного сольватного слоя, который создает потенциальный барьер. Физическая адсорбция всегда сопровождается снижением межфазного натяжения и может привести к образованию структурированного адсорбционного слоя.

3. Структурно-механический фактор присутствует, когда на поверхности частиц образуется структурированный, гелеобразный и обладающий механической прочностью слой из адсорбированных молекул ПАВ и ВМС.

Быстрая и медленная коагуляция

Коагуляция - слипание частиц (образование агрегатов, слияние капель) в свободнодисперсных системах при потере ими агрегативной устойчивости, в результате чего поверхностная энергия уменьшается.

– частичная концентрация дисперсной фазы (число частиц в единице объема);

– стерический фактор ;

– число столкновений частиц в единице объема в единицу времени;

– потенциальный барьер.

В зависимости от величины скорости коагуляции принято различать два вида коагуляции:

1. Быстрая (диффузионная) коагуляция, которая наблюдается при Р = 1, ΔΕ = 0. В этих условиях каждое столкновение двух частиц ведет к их коагуляции (слипанию).

2. Медленная (барьерная) коагуляция, протекающая при 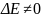. При наличии потенциального барьера скорость коагуляции зависит от величины и может быть очень низкой. Это будет соответствовать кинетически устойчивой системе.

В ывод уравнения Смолуховского.

Для монодиспсрсной системы в условиях быстрой коагуляции в качестве исходных примем следующие условия:

1. В исходном состоянии дисперсная система содержит одинарные, монодисперсные сферические частицы радиусом .

3. Столкновения между частицами обусловлены их участием в броуновском движении

4. 

   Рисунок 27.1 – К нахождению констант уравнения Смолуховского

   Все столкновения частиц эффективны, то есть рассматривается быстрая (диффузионная) коагуляция ( ).

– коэффициент диффузии частиц; 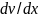– градиент частичной концентрации ;  – расстояние от центра выделенной частицы; – площадь поверхности сферы, так как частицы налетают на центральную частицу со всех направлений.

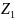– число столкновений, испытываемых одной частицей в единицу времени.

В единице объема содержится всего частиц, и каждая из них испытывает , столкновений. Общее число столкновений в единице объема в единицу времени:

Поскольку рассматривается быстрая коагуляция:

Примем, что является константой для данной дисперсной системы и фактически представляет собой константу скорости быстрой коагуляции.

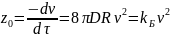
В это уравнение вводят такой параметр, как время половинной коагуляции , то есть время, за которое число частиц уменьшается в два раза. При :

Уравнение Смолуховского ⁴:

29. Теория ДЛФО. Расклинивающее давление и его составляющие. Вывод уравнения для энергии электростатического отталкивания при взаимодействии слабозаряженных поверхностей. Потенциальные кривые взаимодействия частиц для агрегативно устойчивой и неустойчивой дисперсных систем.

Теория ДЛФО является теорией агрегативной устойчивости лиофобных свободнодисперсных систем с жидкой дисперсионной средой. Она была разработана двумя советскими учеными (Б.В. Дерягин, Л.Д. Ландау) и, независимо, двумя учеными из Нидерландов (Е. Фервей, Дж. Овербек).

Расклинивающее давление – сила, действующая между частицами и отнесенная к единице поверхности.

В зависимости от вклада тех или иных сил оно может быть как положительным, так и отрицательным, и при этом его величина зависит от толщины пленки, разделяющей частицы :

• – преобладают силы отталкивания, это говорит о наличии потенциального барьера.

• – между частицами (в общем случае между элементами дисперсной фазы) действуют силы притяжения, и система является агрегативно неустойчивой ( ).

Расклинивающее давление – результат действия сил разной природы. В общем случае его можно представить как сумму нескольких слагаемых:

– молекулярная составляющая, обусловленная действием сил Ван-дер-Ваальса;

– электростатическая составляющая, возникающая при перекрытии диффузных частей двойных электрических слоев;

– структурная составляющая, вызванная перекрытием поверхностных слоев дисперсионной среды, структура которых отличается от структуры в объеме жидкости;

– стерическая составляющая, обусловленная перекрытием адсорбционных слоев, со стоящих из молекул ПАВ и ВМС.

Теория ДЛФО в своем классическом варианте рассматривает только два первых слагаемых уравнения (силы молекулярной и электростатической природы почти всегда действуют между частицами в жидкой среде).

Для вывода уравнения для энергии электростатического отталкивания слабозаряженных поверхностей, рассмотрим плоские параллельные пластины (рис 29.1).

Рисунок 29.1 – Схема взаимодействия двух плоских частиц:

а – без перекрытия диффузных частей ДЭС; б – с перекрытием

Введем ограничения:

1. При сближении частиц происходит перекрытие диффузных частей ДЭС.

2. Рассматриваем случай слабозаряженных частиц , что позволит воспользоваться уравнениями, полученными в рамках теории Гуи-Чепмена.

3. Размер частиц дисперсной фазы (радиус кривизны г) значительно больше толщины диффузной части ДЭС ( ). Это условие озна чает, что мы пренебрегаем кривизной поверхности и фактически рас сматриваем взаимодействие двух плоских полубесконечных пластин.

Для рассматриваемых пластин энергия электростатического отталкивания:

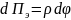
Проинтегрируем это уравнение в пределах от до нуля в соответствии с схемой (рис. 29.1) с учетом решения уравнения Пуассона-Больцмана в рамках теории Гуи-Чепмена получим:

С учетом уравнения Гуи-Чепмена получим:

Чтобы получить уравнение для расчета энергии электростатического отталкивания пластин, нужно проинтегрировать в пределах от до :

Рисунок 29.2 – Характерные формы потенциальной кривой парного взаимодействия частиц

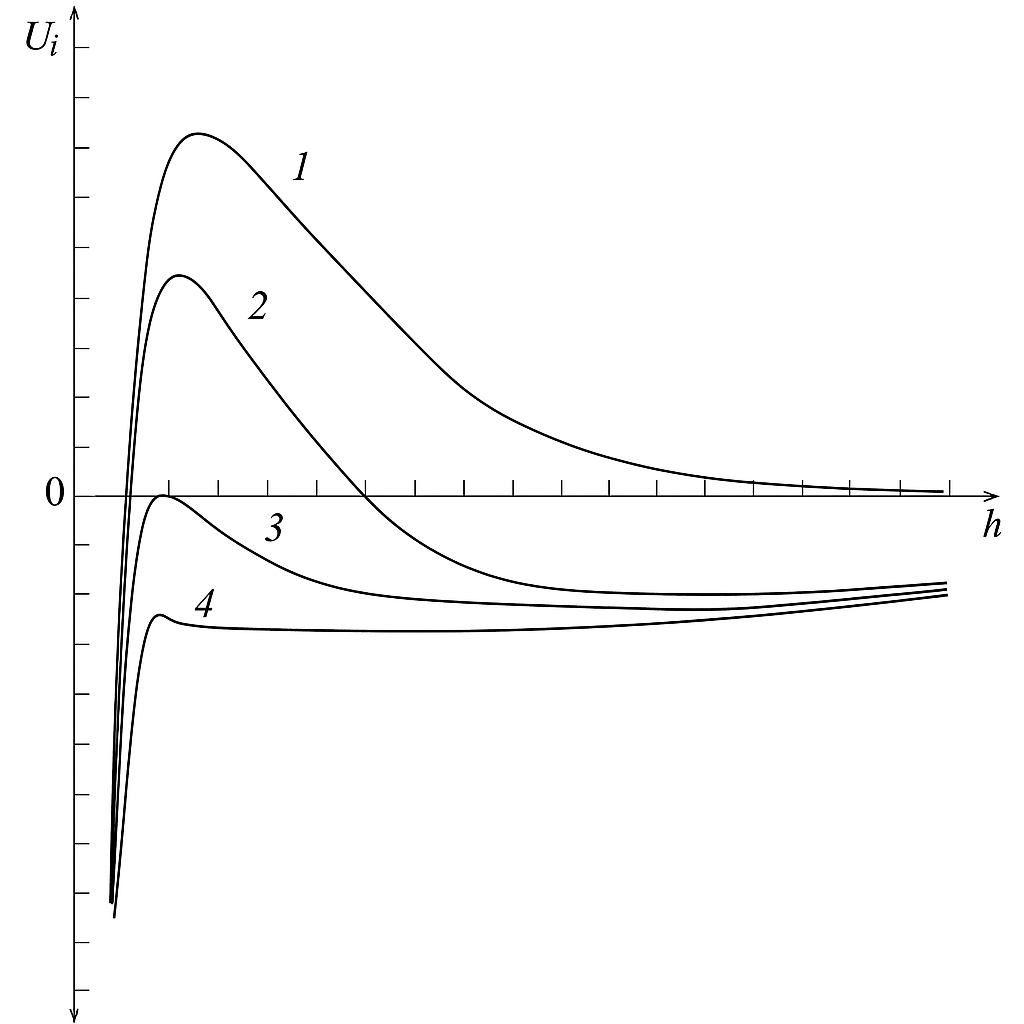П отенциальные кривые взаимодействия частиц для агрегативно устойчивых (рис. 29.2, кривая 1) системы и неустойчивых дисперсных систем (рис. 29.2, кривые 2-4).

Первая потенциальная кривая (рис. 29.2, кривая 1) характеризуется наличием большого потенциального барьера и отсутствием второго минимума. Такая кривая соответствует кинетически устойчивой дисперсной системе, в которой скорость коагуляции может быть пренебрежимо малой, если .

Особенностью кривой 2 (рис. 29.2, кривая 2) является наличие как потенциального барьера , так и второго минимума глубиной . В такой системе будет протекать быстрая коагуляция, если . При этом частицы будут оставаться во втором минимуме, если одновременно 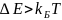, так как их кинетической энергии недостаточно, чтобы «выскочить» из него.

При небольшой величине потенциального барьера становится возможным постепенный переход частиц в первый минимум. Если на всех расстояниях между частицами преобладает действие сил притяжения , (рис. 29.2, кривые 3 и 4), то такая система будет агрегативно неустойчивой. В ней будет протекать быстрая коагуляция, при этом коагулирующие частицы будут попадать в первый минимум.

30. Природа сил притяжения и отталкивания между частицами в дисперсных системах. Вывод уравнения для энергии притяжения между частицами (теория ДЛФО). Константа Гамакера и ее физический смысл. Анализ зависимости суммарной энергии взаимодействия частиц от расстояния между ними.

Силы притяжения в дисперсных системах имеют ван-дер-ваальсовскую природу (дисперсионные взаимодействия Лондона). Они являются универсальными, то есть действуют между всеми частицами, независимо от их заряда.

Силы отталкивания обычно обусловлены электростатическим взаимодействием двойных электрических слоёв (ДЭС) и стерическим, структурным или сольватным отталкиванием, если на поверхности есть адсорбированные молекулы ПАВ или полимеров

Р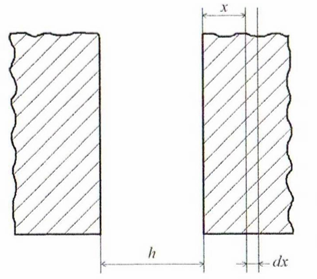 ассмотрим взаимодействие двух полубесконечных пластин и пренебрежем кривизной поверхности

Примем, что энергия взаимодействия каждого атома, находящегося в бесконечно тонком слое, со всеми атомами левой пластины описывается уравнением:

Рисунок 30.1 – К выводу уравнения для энергии молекулярного взаимодействия полубесконсчных пластин

которое было получено для расчета энергии притяжения атома адсорбата к поверхности адсорбента. С этой целью мы умножим энергию взаимодействия одного атома на число атомов в бесконечно тонком слое:

где – константа для данной пары пластин; – площадь поверхности пластины; – число атомов (молекул) в единице объема пластины; – число атомов в слое толщиной .

Интегрирование этого уравнения в пределах изменения от до , то есть по толщине правой пластины, дает соотношение для расчета энергии молекулярного притяжения двух полубесконечных пластин и в расчете на единицу поверхности (в ):

где – так называемая «простая» константа Гамакера, которая и определяет величину энергии притяжения.

При наличии среды учитывают её влияние:

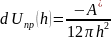
Здесь – cложная константа Гамакера:

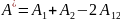
– константа Гамакера для дисперсной фазы;

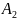– константа Гамакера для дисперсионной среды;

– постоянная, учитывающая взаимодействие дисперсной фазы с дисперсионной средой.

Константа Гамакера определяет интенсивность суммарного дисперсионного взаимодействия между макроскопическими телами, следовательно, по ней можно судить о склонности системы к коагуляции: чем больше сложная константа Гамакера, тем выше склонность к коагуляции.

Запишем выражение для суммарной энергии взаимодействия частиц по теории ДЛФО:

где – энергия притяжения, медленно убывающая при отдалении тел; – энергия отталкивания, быстро убывающая при отдалении тел.

э

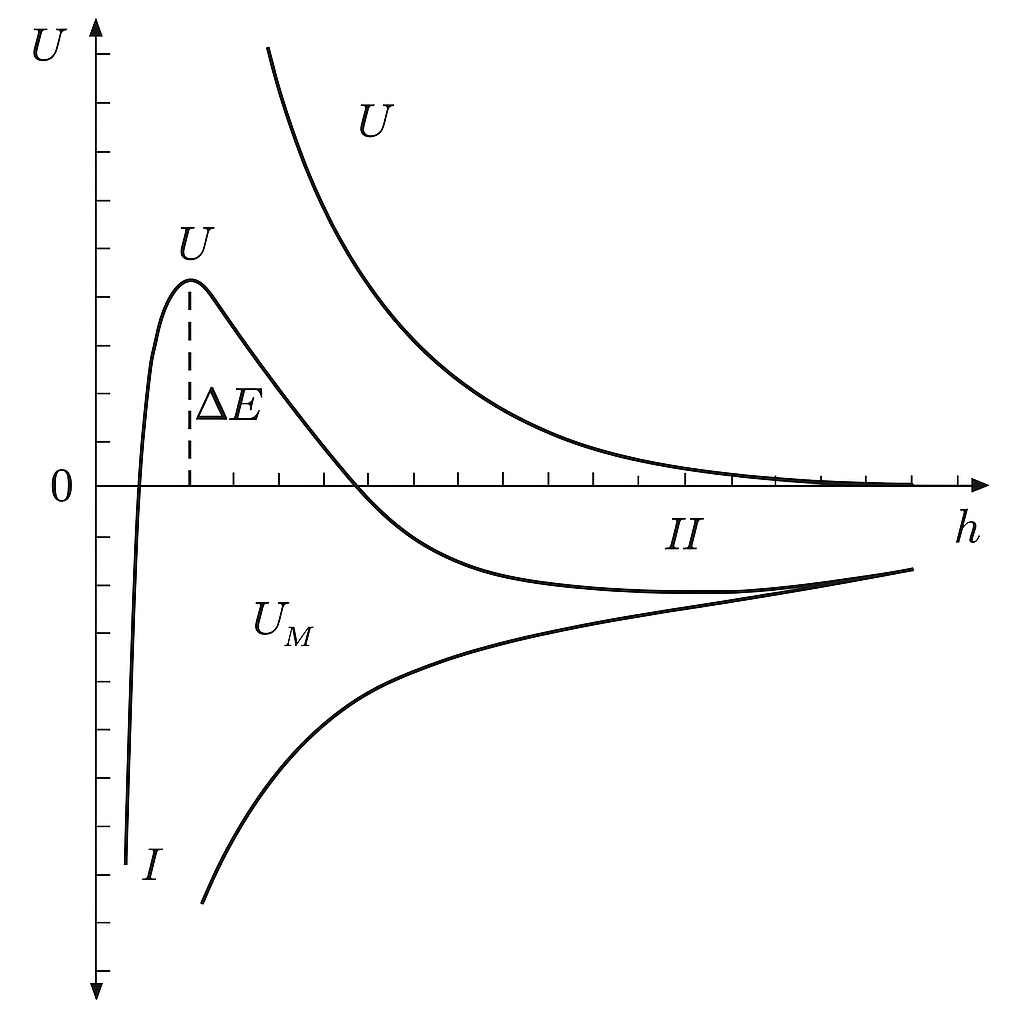
Рисунок 29.2 – Зависимость энергии электростатического отталкивания энергии молекулярного притяжения 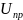и суммарной потенциальной энергии взаимодействия сферических частиц от расстояния между ними (цифрами I и II отмечено положение первого и второго минимума)

31. Факторы агрегативной устойчивости лиофобных дисперсных систем. Электролитная коагуляция (концентрационная и нейтрализационная коагуляция). Правило Шульце-Гарди и закон Дерягина. Способы стабилизации лиофобных дисперсных систем.

По механизму коагулирующего действия электролиты делят на индифферентные и неиндифферентные.

Неиндифферентные – электролиты, ионы которых одинаковые по знаку заряда с противоионами ДЭС дисперсной системы, способны адсорбироваться в слое Гельмгольца, нейтрализуя заряд потенциалопределяющих ионов. Это ведет к снижению абсолютного значения , падению величины и росту скорости коагуляции ( . Нейтрализационная коагуляция вызывается добавками неиндифферентных электролитов.

Индифферентные – электролиты, содержащие простые однозарядные ионы, типа . Введение индифферентных электролитов на величину влияет слабо в виду плохой адсорбции их ионов в слое Гельмгольца, но они уменьшают величину (сжимают диффузный слой) за счет увеличения ионной силы дисперсионной среды. При падении величины растет значение , уменьшаются и 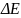, скорость коагуляции растет.

Концентрационная коагуляция вызывается добавками индифферентных электролитов.

Закон Дерягина («закон шестой степени» Дерягина)

В этом законе потенциал диффузного слоя не фигурирует, так как при большой величине потенциала поверхности энергия отталкивания перестает зависеть от величины :

В соответствии с законом Дерягина пороги быстрой коагуляции в присутствии одно-, двух- и трехзарядных противоионов соотносятся следующим образом:

Правило Шульце-Гарди. В соответствии с этим эмпирическим правилом эти же пороги быстрой коагуляции находятся в соотношении .

Способы стабилизации – создание поверхностных слоев, которое ведет к образованию коагуляционных контактов за счет добавления ПАВ (что способствует мицеллообразованию) или электролитов (они взаимодействую с ДЭС).

32. Структурообразование в соответствии с теорией ДЛФО. Коагуляционно-тиксотропные и конденсационно-кристаллизационные структуры. Условия перехода одних структур в другие. Классификация дисперсных систем по реологическим (структурно-механическим) свойствам.

Структуры первого типа образуются в дисперсных системах в результате коагуляции (появление контактов между частицами). Поскольку структурообразование первого типа представляет собой частный случай коагуляции, то к этому можно подойти с позиций теории ДЛФО.

В соответствии с двумя минимумами на потенциальной кривой, по предложению П.А. Ребиндера, различают два класса структур, возникающих в дисперсных системах.

Коагуляционные структуры возникают если на потенциальной кривой есть большой потенциальный барьер и глубокий второй минимум , то в такой системе возникает структура, в которой частицы находятся во втором минимуме. В местах контакта частицы будут разделены прослойкой дисперсионной среды (поверхностными слоями), поскольку положение второго минимума соответствует расстояниям порядка десятков нанометров. Коагуляционные контакты (рис. 32.1, а) и структура являются непрочными и обратимыми, так как между частицами в этом случае действуют только молекулярные силы, преимущественно дисперсионные.

При механическом воздействии на систему (например, при перемешивании) коагуляционная структура легко разрушается, что со провождается падением вязкости, но с течением времени структура, как и вязкость, самопроизвольно восстанавливаются. Это явление получило название тиксотропии. В связи с этим структуры этого класса называют еще и коагуляционно-тиксотропными.

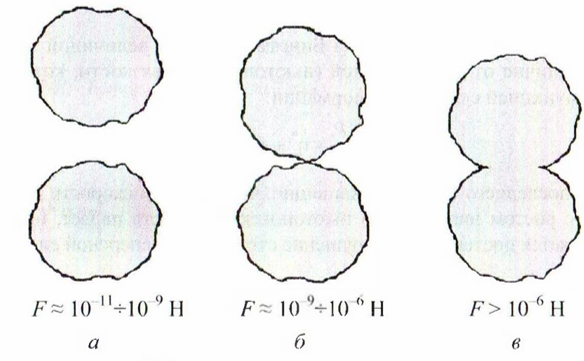
Рисунок 32.1 – Типы контактов между частицами:

а – коагуляционный; б – атомный; в – фазовый

П ри небольшой высоте потенциального барьера и неглубоком втором минимуме частицы могут постепенно переходить в первый минимум. Они сразу будут попадать в этот минимум при 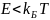. При этом между частицами сначала возникают атомные контакты, то есть площадь контакта двух частиц ограничена одной атомарной ячей кой. Эти контакты значительно прочнее коагуляционных, потому что между частицами в этом случае действуют валентные силы, но на первом этапе остаются обратимыми.

Атомные контакты, как правило, трансформируются в фазовые контакты, то есть частицы «срастаются» (рис. 32.1, б, в). Скорость перехода одних контактов в другие зависит от условий и свойств системы. Причиной срастания частиц может быть выделение твердой фазы из пересыщенной дисперсионной среды (например, при гидратационном твердении бетона), изотермическая перегонка, оплавление и частичное испарение частиц в процессах спекания. В местах фазовых контактов частиц кривизна поверхности отрицательна, что способствует их дальнейшему срастанию и упрочнению. Прочность фазовых контактов наибольшая, по сравнению с атомными и коагуляционными, и фактически определяется прочностью самих частиц. Эти контакты разрушаются необратимо. Примерные диапазоны прочности (сила , необходимая для разрыва контакта) соответствующих контактов указаны на рис. 32.1.

Структуры, в которых между частицами имеются фазовые контакты, относят ко второму классу структур и называют в общем случае конденсационно-кристаллизационными. Если фазовые контакты воз никли в результате процессов конденсации, а частицы являются аморфными, то структура называется конденсационной.

Структуру, возникшую в результате срастания кристаллических частиц, называют кристаллизационной.

В зависимости от наличия или отсутствия предела текучести 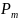все дисперсные системы делят на твердообразные и жидкообразные . В свою очередь, жидкообразные системы делят на ньютоновские и неньютоновские системы.

Среди неньютоновских систем различают стационарные неньютоновские и нестационарные неньютоновские системы. Различие между этими группами заключается в том, что вязкость стационарных неньютоновских систем зависит от напряжения сдвига , при котором eе измеряют, а вязкость нестационарных неньютоновских систем зависит как от напряжения сдвига, так и от времени измерения вязкости .

Условия перехода. Система может перейти только из второго энергетического минимума в первый (рис. 32.1). Это сможет быть сделано с разрушением поверхностных слоев за счет увеличения энергии системы для преодоления энергетического барьера, например с помощью увеличения температуры.