6. Массообменные процессы.

6.1. Роль массообменных процессов в химической технологии. Общие признаки.

Массообменные процессы являются наиболее распространенными в химической технологии и включают перегонку, ректификацию, абсорбцию, адсорбцию, экстракцию, сушку, кристаллизацию.

Массообменные процессы используются для решения задач разделения жидких и газовых гомогенных смесей, их концентрирования; для защиты окружающей среды (прежде всего для очистки отходящих газов и сточных вод).

Общие признаки массообменных процессов:

- все массообменные процессы применяются для разделения гомогенных смесей компонентов;

- протекают на поверхности раздела фаз (на поверхности паровой (газовой) и жидкой фаз осуществляются процессы перегонки, ректификации, абсорбции; на поверхности раздела двух жидкостей протекает жидкостная экстракция; на поверхности раздела газовой и твердой фаз протекают процессы адсорбции, сушки и т. д.);

- скорость протекания массообменных процессов определяется диффузией распределяемого вещества во взаимодействующих фазах;

- движущая сила массообменных процессов выражается разностью концентраций или парциальных давлений распределяемого вещества;

- все массообменные процессы обратимы. Направление перехода вещества определяется концентрациями вещества в фазах и условиями равновесия;

- переход вещества из одной фазы в другую возникает самопроизвольно и завершается установлением подвижного фазового равновесия.

Механизм процессов переноса массы вещества определяется состоянием поверхности раздела фаз. По этому принципу массообменные процессы подразделяются:

- на процессы и аппараты в системах со свободной границей раздела фаз (газ – жидкость, пар – жидкость, жидкость – жидкость).

- на процессы и аппараты в системах с неподвижной поверхностью контакта фаз (газ (пар) – твердое тело, жидкость – твердо тело);

- мембранные процессы, в которых поверхностью раздела фаз является полупроницаемая перегородка (мембрана).

6.2. Термодинамическое равновесие.

Термодинамическое равновесие рассмотрим на примере разделения аммиачно – воздушной смеси (газовая фаза G) с водой (жидкая фаза L); принимая во внимание хорошую растворимость аммиака в воде, то есть переходит из фазы G в фазу L.

Обозначим:

У_н – начальная концентрация аммиака в газовой фазе,

Х_н – начальная концентрация аммиака в жидкой фазе. Предположим, что х_н=0.

При взаимодействии фаз G и L концентрация аммиака в газовой фазе уменьшается, а в жидкой – возрастает. С началом растворения аммиака в воде начинается переход части его молекул в обратном направлении. С течением времени скорость перехода аммиака в фазу L (процесс растворения аммиака в воде) снижается, а скорость обратного процесса (выделение аммиака из фазы L и переход в фазу G) возрастает. Такой двусторонний переход будет продолжаться до тех пор пока скорости переноса в обоих направлениях не станут равными. Если температуры взаимодействующих фаз G и L различны, то имеет место и перенос тепла. При равенстве скоростей прямого и обратного процессов устанавливается термодинамическое равновесие. Система, находящаяся в этом состоянии, называется равновесной.

Равновесная система характеризуется равновесными концентрациями распределяемого компонента в фазах (в рассматриваемом приере распределяемым компонентом является аммиак; воздух и вода распределяющие компоненты или носители).

Таким образом, концентрация аммиака в газовой фазе уменьшается от у_н до У_р; в жидкой фазе – возрастает от 0 до х_р.

Между равновесными концентрациями распределяемого компонента в фазах устанавливается взаимосвязь, общий вид которой выражается зависимостью:

y_р=f(x) или x_p=f(y) (6.1)

так как в условиях равновесия некоторому значению х соответствует определенное значение у_р и наоборот.

Графическое изображение зависимостей (6.1) называется линией равновесия, которая является кривой либо в частном случае – прямой линией. На рисунке 6.1 показана кривая равновесия при постоянных значениях давления. (П) и температуры (t) для системы с компонентами - носителями.

1

Рисунок 6.1 – Диаграмма равновесия при П=const и t=const.

Любая точка, лежащая на кривой равновесия характеризует концентрацию распределяемого компонента в равновесной газо – жидкостной системе.

Отношение равновесных концентраций фаз называется коэффициентом распределения

m=у_р/х (6.2)

Для разбавленных растворов коэффициент распределения является величиной постоянной, поэтому линия равновесия близка к прямой, тангенс угла наклона которой равен величине m.

6.3.Основные закономерности массопередачи.

Закономерности массопередачи рассмотрим на примере взаимодействия аммиачно – воздушной смеси (фаза G) и воды (фаза L). Фазы в противотоке движутся с некоторой скоростью относительно друг друга и разделены подвижной поверхностью фаз (свободная граница раздела фаз).

Предположим, что распределяемого компонента (аммиака) происходит в условиях турбулентного движения фаз, причем аммиак переходит из фазы G, где его концентрация больше равновесной (у>у_р), в фазу L, в которой его концентрация меньше равновесной (х<х_р).

Таким образом осуществляется процесс массоотдачи из фазы G к поверхности раздела фаз и процесс массоотдачи от поверхности раздела в фазу L. В результате этих частных процессов и преодоления сопротивления переносу через поверхность раздела фаз происходит процесс массопередачи – переход компонента из одной фазы в другую. Схема массопередачи изображена на рисунке 6.2.

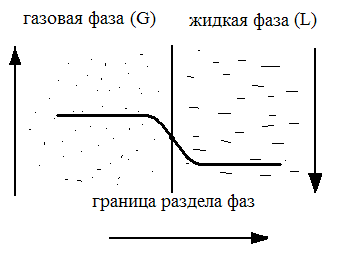
Рисунок 6.2 – Схема массопередачи и профиля изменения концентрации компонента в турбулентном потоке.

Процесс массопередачи тесно связан с гидродинамической структурой потока в каждой фазе. При турбулентном режиме движения в каждой фазе можно выделить ядро, или основную массу фазы, и пограничный слой у поверхности раздела фаз. В ядре потока в силу турбулентных пульсаций концентрация распределяемого компонента практически постоянна. В пограничном слое турбулентность затухает, что приводит к резкому изменению концентрации по мере приближения к поверхности раздела. Непосредственно у поверхности перенос сильно замедляется, так как его скорость определяется скоростью молекулярной диффузии.

Известно, что при переносе субстанции (в данном случае массы вещества) можно выделить два механизма – молекулярный и конвективный. При турбулентном движении в ядре потока фазы массоперенос к поверхности раздела фаз (или в противоположном направлении) осуществляется в основном конвективной диффузией. В пограничном слое скорость массопереноса лимитируется скоростью молекулярной диффузии. Для интенсификации массопереноса необходимо повышать степень турбулентности потока ( например, увеличивая скорость фаз до некоторого предела), уменьшая толщину пограничного слоя.

Для системы, находящейся в равновесии, концентрации распределяемого компонента у границы раздела фаз равны равновесным, то есть:

у_гр=у_р; х_гр=х_р.

Молекулярная диффузия.

Перенос массы вещества молекулярной диффузией описывается первым законом Фика, уравнение которого для поверхности диффузии F имеет вид:

, (6.3)

Где D – коэффициент диффузии, м²/с;

F – поверхность, нормальная к направлению диффузии, м²;

- градиент концентрации вещества, кг/м³ на единицу длины пути n диффундирующего вещества;

Первый закон Фика формируется так:

масса вещества, диффундирующего в единицу времени через поверхность прямопропорциональна величине поверхности и градиенту концентраций.

Знак минус в уравнении (6.3) учитывает уменьшение по длине пути диффузии.

Коэффициент молекулярной диффузии D зависит от природы диффундирующего вещества и характеризует способность его проникать в какую – либо среду

Коэффициент D зависит от температуры (возрастает с увеличением температуры), а для газов – еще и от давления (снижается с увеличением давления).

Для газовой фазы Dг=1 см²/сут; откуда следует, что молекулярная диффузия в жидкостях, а тем более в твердых телах – процесс очень медленный.

Числовые значения коэффициента диффузии приведены в справочной литературе.

6.4. Уравнение массоотдачи.

В пределах каждой из взаимодействующих фаз перенос распределяемого вещества осуществляется конвективной диффузией (в ядре потока) и молекулярной (в пограничном слое). Однако использование закона Фика (уравнение (6.3)) для определения массопереноса молекулярной диффузией затруднительно, так как закон распределения концентраций в пограничном слое ( ) неизвестен. Поэтому уравнение массоотдачи имеет вид:

(6.4)

Где М – масса вещества, перенесенного за единицу времени, кг/с;

F – поверхность раздела фаз, м²;

- движущая сила в пределах фазы, равная разности концентраций в ядре фазы и на поверхности раздела фаз (или наоборот в случае обратного направления переноса).

Если распределяемый компонент переходит из фазы G в фазу L (рисунок 6.2), то уравнение массоотдачи имеет вид:

- для газовой фазы G

(6.5)

- для жидкой фазы L

(6.6)

В уравнениях (6.4) – (6.6) коэффициент пропорциональности называется коэффициент массоотдачи, который учитывает как молекулярный, так и конвективный перенос в фазе. Коэффициент имеет размерность:

, т.е. размерность будет определяться способом выражения состава фазы.

Коэффициент массоотдачи показывает массу вещества, переходящего от едницы поверхности раздела фаз в ядро потока (или наоборот) в единицу времени при движущей силе, равной единице.

Коэффициент массоотдачи является кинетической характеристикой фазы и зависит от многих факторов:

- физических свойств фазы (плотность, вязкость и др.)

- гидродинамических условий (ламинарный или турбулентный режим течения), связанных с физическими свойствами среды, а также конструкцией и геометрическими размерами массообменного аппарата.

По своему смыслу коэффициент массоотдачи является аналогом коэффициента теплоотдачи в процессах переноса тепла, а уравнение массоотдачи идентично по структуре уравнению теплоотдачи.

6.5 Подобие массообменных процессов

Связь между переменными, характеризующими процесс массоотдачи в потоке фазы, устанавливает система уравнений, включающая дифференциальное уравнение конвективной диффузии и уравнения движения (уравнение Новье-Стокса и неразрывности потока). Расчет такой системы возможен лишь при существенных её упрощениях. Поэтому для решения этой задачи используют методы теории подобия.

Идентичность математических описаний теплообмена и массообмена позволяет полагать аналогию при составление обобщенного (критериального) уравнения массоотдачи.

Критериальное уравнение массоотдачи для неустановившегося процесса имеет вид:

(6.7)

Здесь:

- диффузионный критерий Нуссельта, является определенным, так как содержит определяемый коэффициент теплоотдачи и характеризует отношение скорости переноса вещества (конвективного и молекулярного - ) к молекулярному переносу (D) при определяющем геометрическом размере ;

- диффузионный критерий Фурье, который характеризует подобие неустановившихся процессов массобмена;

- критерий Рейнольдса, характеризующий гидродинамический режим движения фазы;

- диффузионный критерий Прандтля, характеризующий отношение профиля скоростей (через ) к профилю концентраций (через D), т.е. отношение толщины гидродинамического и диффузионного пограничных слоев;

- модифицированный критерий Галилея;

Здесь:

- критерий Фруда, отражающий влияние сил тяжести при движение фаз; - геометрический симплекс.

При установившемся движении ( ) и при отсутствии влияния сил тяжести ( )

, (6.8)

Например:

, (6.9)

где определяют экспериментальным путем.

6.6. Основное уравнение массопередачи.

Для установившегося процесса основное уравнение массопередачи имеет вид:

(6.10)

где - масса вещества, перешедшего из одной фазы в другую в единицу времени, ;

- поверхность взаимодействия фаз, м²;

- средняя движущая сила процесса;

- коэффициент пропорциональности, характеризующий скорость массопередачи.

Коэффициент пропорциональности к по аналогии с теплопередачей называется коэффициентом массопередачи и имеет размерность:

.

Коэффициент массопередачи показывает массу распределяемого компонента, переходящего из одной фазы в другую в единицу времени через единицу поверхности раздела фаз при движущей силе, равной единице.

Запишем уравнение (7.10) для каждой из взаимодействующих фаз:

- для фазы G

(6.11)

- для фазы L

(6.12)

Коэффициент массопередачи k зависит от коэффициентов массоотдачи и . Для выявления этой связи принимают, что на границе поверхности раздела фаз (см.рисунок 6.2) достигается равновесие ( ), поэтому сопротивлением переносу через границу раздела фаз можно пренебречь. Тогда для расчета коэффициента массопередачи можно получить уравнения:

- в концентрациях газовой фазы

(6.13)

- в концентрациях жидкой фазы

(6.14),

которые называются уравнениями аддитивности фазовых сопротивлений.

Доля диффузионного сопротивления каждой фазы зависит от гидродинамических условий и значения коэффициента диффузии D в ней, а также от условий равновесия. В некоторых случаях диффузионное сопротивление одной из фаз может быть пренебрежимо мало по сравнению с сопротивлением другой. Предположим, что сопротивление фазы L мало. Тогда коэффициент очень велик, а диффузионное сопротивление соответственно очень мало. При данном значении коэффициента распределения отношение в уравнении (6.13) мало. Тогда , т.е. в данном случае скорость массопередачи ограничена сопротивлением в фазе G, которое является определяющим.

В противоположном случае, когда мало сопротивление фазы G, величина велика, а отношение незначительно. Тогда из уравнения (6.14) коэффициент , т.е. определяющим является сопротивление в фазе L.

Для интенсификации массопередачи надо по возможности увеличивать значение того коэффициента массоотдачи , который лимитирует величину . Увеличение можно достичь (припрочих равных условиях) путем увеличения скорости потока соответствующей фазы, однако необходимо учитывать одновременное увеличение расхода энергии на проведение процесса.

В расчетах массообменных аппаратов часто используют коэффициенты массоотдачи, отнесенные к рабочему объему аппарата, т.е. объемные коэффициенты массоотдачи и массоотдачи .

Объемные коэффициенты массоотдачи определяются по уравнениям:

(6.15)

Объемные коэффициенты массопередачи определяются по уравнениям:

; (6.16)

В уравнениях (6.15) и (6.16) - удельная поверхность контакта фаз, т.е. поверхность, отнесенная к единице рабочего объема аппарата, .

Движущей силой массообменных процессов ( ) является разность между рабочими и равновесными концентрациями распределяемого компонента.

Для рассмотренного в пункте 1 примера движущая сила по газовой фазе выразится так: ; по жидкой .

Движущая сила характеризует степень отклонения системы от равновесия. При установление равновесия между фазами массообмен прекращается.

Рассмотрим расчет движущей силы в массообменном аппарате со структурой потоков, соответствующих модели идеального вытеснения; фазы движутся противоточно; рабочие концентрации распределяемого компонента по поверхности F массопередачи изменяется от до (по газовой фазе) и от до (по жидкой фазе) (рисунок 6.3а)

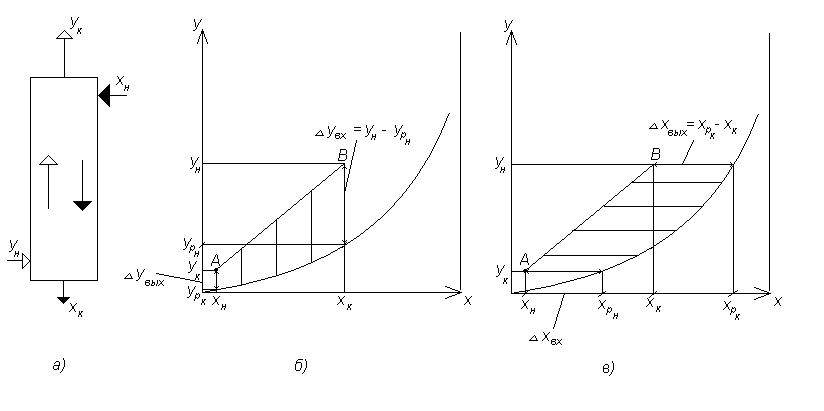
а – схема потоков в противоточном массообменном аппарате; б,в – выражение движущей силы массообменного процесса.

Рисунок 6.3 – Определение движущей силы противоточного процесса массопередачи.

Зависимость между рабочими концентрациями распределяемого компонента в фазах изображается линией, которая называется рабочей линией процесса. Вид функции или уравнение рабочей линии можно получить из уравнения рабочей линии можно получить из уравнения материального баланса и в общем виде записывается так:

(6.17)

В координатах рабочая линия представляет собой прямую, ограниченную точками с координатами и (т. А, верхний конец аппарата, рисунок 1б, в) и и (т. В, нижний конец аппарата). Так как (распределяемый компонент переходит из газовой фазы в жидкую), то рабочая линия АВ располагается выше кривой равновесия.

Из рисунка (6.3 б, в) видно, что движущая сила для каждого сечения аппарата изменяется. Поэтому в расчетах массообменного процесса используется средняя движущая сила ( ), которую по аналогии с тепловыми процессами можно рассчитать по уравнениям:

- для газовой фазы

; (6.18)

- для жидкой фазы

;

где и - большая, а и - меньшая разности концентрации на концах массообменного аппарата.

При <2 движущая сила определяется как среднеарифметическое, т.е.

(6.19)

Движущую силу массообменного процесса можно выразить разностью парциальных давлений распределяемого компонента

- по газовой фазе ,

- по жидкой фазе

где - парциальное давление распределяемого компонента в равновесной системе;

- парциальное давление, соответствующее рабочим концентрациям распределяющего компонента в фазах.

Движущая сила характеризует направление массопередачи. Распределяемое вещество всегда переходит из фазы, где его концентрация этого вещества ниже равновесной. Если, например, и , то распределяемый компонент будет переходить из жидкой фазы (L) в газовую (G).

Применение правила Гиббса в процессах массообмена.

Существование фаз равновесной системы возможно лишь при определенных условиях. При изменении этих условий равновесие системы нарушается и имеет место переход вещества из одной фазы в другую.

Количество параметров, изменение которых не нарушает равновесия системы, определяется правилом фаз или законом равновесия фаз Гиббса

С=К+2-Ф (6.20)

где С – число степеней свободы или независимых параметров (температура, давление, концентрация), значение которых можно изменять в определенных пределах, не нарушая равновесия системы;

К – число компонентов системы;

Ф – число фаз системы;

2 – число внешних факторов, влияющих на положение равновесия в системе (для массопереноса внешними факторами являются температура и давление).

Рассмотрим применение правила фаз Гиббса для некоторых частных случаев.

1. Однокомпонентная паро-жидкостная равновесная система (например, насыщенный водяной пар)

Число степеней свободы

С = 1+2–1=1

т.е давление насыщенных паров воды (Р) зависит лишь от температуры. Таким образом, для любого другого компонента (i-го) можно записать

P_i=f(t) (6.21)

Для большинства компонентов зависимость (6.21) приведена в справочной литературе. Для аналитического расчета широко применяется эмпирическое уравнение Антуана

, (6.22)

где A_i, B_i, C_i – коэффициент Антуана, значение которых для индивидуальных компонентов приведены в справочной литературе.

2. Однокомпонентная равновесная система, состоящая из трех фаз (пар – жидкость – твердое тело) не имеет степеней свободы (С=1+2-Ф=0). Например, система вода – лед – водяной пар находится в равновесии только при давлении 610,6 Па и температуре 0,0076 ^оС

3. Двухкомпонентная равновесная парожидкостная равновесная система имеет две степени свободы (С=2+2-2=2).

В этом случае о переменных (например, давлением) задаются и получают однозначную зависимость между температурой и концентрацией или (при постоянной температуре) – между давлением и концентрацией. Зависимость между параметрами (температура – концентрация, давление – концентрация) строят в плоских координатах. Такие диаграммы называют фазовыми или диаграммами состояния.

Некоторые законы идеальных газов и растворов

Идеальной называется система, паровая фаза которой является идеальным газом, а жидкая – идеальным раствором.

Идеальным считается газ, состоящий из упругих молекул, между которыми отсутствует силы межмолекулярного взаимодействия и размеры которых пренебрежимо малы по сравнению с межмолекулярным объемом.

Состояние идеального газа можно описать уравнением Менделеева-Клайперона

P_iV_i=N_iRT (6.23)

где P_i – абсолютное (или парциальное) давление i-го компонента.

V_i – абсолютный объем

N_i – число молей i-го компонента. (здесь g_i – масса i-го компонента; M_i – его мольная масса);

R – универсальная газовая постоянная (при Т_о=273К и П_о=0,1 МПа R=8314 Дж/(моль·град));

Т – абсолютная температура, К.

Смесь идеальных газов подчиняется законом аддитивности парциальных давлений и парциальных объемов.

- парциальным давлением компонента (Р_i) газовой смеси называют давление, которое имел бы компонент, находясь при температуре и давлении смеси, при условии, что все другие компоненты удалены.

В соответствии с законом аддитивности давление (П) смеси идеальных газов равно сумме парциальных давлений компонентов

(6.24)

где n – число компонентов газовой смеси.

- парциальным объемом компонента (V_i) газовой смеси называется объем, которой занимал бы компонент, находясь при температуре и давлении смеси, при условии, что все другие компоненты удалены.

В соответствии с законом аддитивности объем (V_m) смеси идеальных газов равен сумме парциальных объемов компонентов

(6.25)

Запишем уравнение Менделеева-Клайперона (6.23) для i-го компонента газовой смеси при условии V_i=V_m и для смеси газов (с учетом уравнений 6.24 и 6.25)

где N_m – число молей компонентов смеси.

Разделим левые и правые части уравнений системы.

(6.27)

Выражение (6.27) есть математическое выражение закона Дальтона, согласно которому парциальное давление компонента газовой смеси равно произведению общего давления компонента на мольную долю компонента в смеси.

Запишем уравнение Менделеева-Клайперона (6.23) для двух компонентов газовой смеси (при условии V_i=V_m)/

После несложных преобразований можно получить уравнение Авогадро-Дальтона

(6.28)

согласно которому массовое соотношение компонентов газовой смеси равно отношению произведений их парциальных давлений на мольную массу.

Идеальным считается раствор, при образовании которого не наблюдается теплового эффекта.

К идеальным растворам применим закон Рауля, согласно которому парциальное давление пара i-го компонента (Р_i) над раствором равно произведению давления насыщенного пара чистого компонента (Р_i) при температуре раствора на его мольную долю в жидкой фазе ( ).

Математически закон Рауля можно записать

P_i=Л_i - парожидкостное равновесие идеальных систем (6.29)

Одним из условий равновесия парожидкостной системы является равенство парциальных давлений компонентов во взаимодействующих фазах. Поэтому с учетом законов Дальтона (уравнение 6.27) и Рауля (уравнение 6.29) можно записать выражение

, (6.30)

которое называется уравнение уравнением паро-жидкостного равновесия идеальной системы или уравнением Рауля-Дальтона.

Разделив уравнение (6.30) на общее давление системы П, получим

, (6.31)

в котором отношение Л_i/П называется константой фазового равновесия i–го компонента и обозначается буквой k.

Тогда уравнение (6.31) можно записать в виде выражения

(6.32)

Числовое значение константы фазового равновесия k можно определить по вышенаписанному выражению, либо графически по номограмме

Уравнение изотермы жидкой и паровой фаз равновесной системы

Компоненты бинарной системы отличаются физико-химическими свойствами. Компонент, имеющий при данном давлении более низкую температуру кипения, называется низкокипящим и обозначается НКК, обозначается индексом 1. Компонент, имеющий при том же давлении более высокую температуру, называется высококипящим (ВКК) и все, что к нему относится, обозначается индексом 2.

Запишем уравнение (6.31) по НКК и ВКК бинарной системы и просуммируем левые и правые части полученной системы уравнений

(6.33)

или (6.34)

Уравнение (6.34) называется уравнением изотермы жидкой фазы бинарной равновесной системы и позволяет определить состав жидкой фазы

(6.35)

6. Диаграммы состояния бинарных систем

6.1 Изобарная диаграмма равновесия

Для технических расчетов наиболее важной является диаграмма, связывающая температуру системы с составом паровой и жидкой фаз при постоянном давлении (П=const).

Для построения изобарной диаграммы (рисунок 6) определяются температуры кипения низкокипящего компонента (t_нкк) и высококипящего (t_вкк) при известном значении давления П.

1 – линия кипения; 2 – линия конденсации

Рисунок 6.1. Изобарная диаграмма равновесия

Полученный интервал температур кипения компонентов делится на несколько малых (t₁,t₂,t₃ и т.д.) и для каждого значения температур по справочнику либо по уравнению Антуана (уравнение 6.22) определяются давления насыщенного пара компонентов Л₁ и Л₂. Затем по уравнению изотермы жидкой фазы (уравнение 6.35) определяют состав жидкой фазы (х₁,х₂ и т.д.), соответствующий определенной температуре, а по уравнению (6.31) – состав паровой фазы ( и т.д.) По полученным точкам строят линии кипения жидкости (кривая

t_нккg₁g₂tвкк) и конденсации паров (кривая t_нккG₁G₂tвкк). Отрезки g₁G₁; g₂G₂ и т.д. являются изотермами.

Точки, лежащие на линии кипения (g₁;g₂ и т.д.) соответствуют жидкой фазе, находящейся при температуре кипения. Любая точка, находящаяся ниже этой кривой, характеризует недогретую до температуры кипения жидкую фазу. Аналогично, любая точка, лежащая выше кривой конденсации (линия 2) характеризует систему, состоящую из паровой фазы (перегретый пар). Точки, находящиеся между кривыми кипения и конденсации (например, точка F на рисунке 6) соответствуют равновесным парожидкостным системам.

Изотермы g₁G₁; g₂G₂ и т.д., характеризующие состав равновесных жидкой и паровой фаз, называются нодами или конодами.

6. 2.Диаграмма равновесных составов

Диаграмма равновесных составов связывает составы паровой и жидкой фаз при определённых значениях давления и температуры системы. Линию равновесия можно построить по методике, изложенной в пункте 6. 1, либо аналитически.

Для аналитического расчета линии равновесия запишем уравнение (6.31) для НКК и ВКК бинарной системы

Разделив левые и правые части уравнений, получим выражение

(6.38)

в котором отношение давления насыщенных паров компонентов называется коэффициентом относительной летучести и обозначается буквой , т.е.

(6.39)

Поскольку давление насыщенных паров P₁ и Р₂ низко- и высококипящих компонентов изменяются в интервале температур t_нкк и t_вкк смеси, то для упрощения расчетов используют среднегеометрическое значение коэффициента относительной летучести

(6.40)

где и - относительные летучести при температурах t_нкк и t_вкк.

Коэффициент относительной летучести при понижение температуры обычно увеличивается.

С учетом уравнений (6.39) и (6.40) из уравнения (6.38) получаем выражение

(6.41)

которое позволяет построить линию равновесия (рисунок 6. )

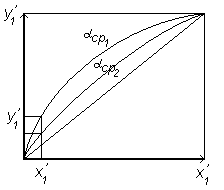
Рисунок 6.2. К определению влияния коэффициента летучести на положение линии равновесия.

Из уравнения (6.41) следует зависимость обогащения паровой фазы низкокипящим компонентом (y₁^’) от коэффициента относительной летучести: при увеличении возрастает. На рисунке 6.2

Диаграммы состояния можно построить, выражая состав равновесных фаз в массовых долях. Для пересчета концентраций используют уравнение

(6.42)

где M_i – мольная масса i-го компонента смеси.

Для бинарной смеси относительно концентрации НКК уравнение (6.42) записывается в виде

Мольную концентрацию i-го компонента по известной массовой концентрации (в долях) можно определить по уравнению

(6.43)

Взаимное положение кривых на изобарной диаграмме (t - x,y) и диаграмме равновесных составов (y - x) соответствует закону Коновалова, который устанавливает связь между изменениями состава, давления или температуры в двухфазных системах.

Закон Коновалова гласит, что пар всегда более обогащен НК, чем соответствующая ему равновесная жидкая фаза.

На рисунке 6.2. при концентрации НКК в паровой фазе больше, чем в жидкой ( ). Аналогичный вывод можно сделать и по рисунку 6.2. Это положение лежит в основе теории перегонки и ректификации бинарных смесей.

Влияние давления на взаимное положение кривых на диаграммах состояния рассмотрим на примере смеси бензол-толуол при П=0,1 0,5 и 1,0 МПа.

а – изобарная диаграмма;

б – диаграмма равновесных составов

Рисунок 6.3 Взаимное положение кривых равновесия при различных давлениях

Из рисунка 6.3. видно, что при одном т том же составе жидкой фазы (х₁) наибольшая концентрация НКК в паровой фазе (у₁) соответствует давлению П=0,1 МПа. Повышение давления снижает степень обогащения паровой фазы низкокипящим компонентом. Это обстоятельство используют при разделении смесей путем перегонки и ректификации.

На практике чаще приходится иметь дело с неидеальными системами, поведение которых отличается от идеальных систем и они, как правило, строятся по справочным или экспериментальным данным (рисунки 6. и 6. ).

Для двухкомпонентного идеального раствора при постоянной температуре ( t=const) парциальные давления компонентов Р₁ и Р₂ и общее давление паров П = Р₁+Р₂ подчиняется закону Рауля, изотерма жидкой фазы изображается прямой (линия 1, рисунок 6. , I, a).

Реальные жидкие смеси могут значительно отклоняться от закона Рауля. Эти отклонения могут быть либо положительными, когда парциальные давления компонентов (Р₁,Р₂) и общее давление (П) выше, чем для идеальных растворов, либо отрицательными, когда Р₁;Р₂ и П меньше, чем следует из закона Рауля. Степень отклонения реальной системы выражается величиной коэффициента активности γ, и уравнения Рауля имеет вид

(6.44)

Для растворов с положительным отклонением от закона Рауля γ>1, для растворов с отрицательным отклонением γ<1.

Растворы с незначительным положительным или отрицательным отклонением от закона Рауля называются растворами нормального типа. Для них всегда соблюдается условие Р₁<П<P₂. Диаграммы парожидкостного равновесия таких систем приведены на рисунке 6. , II.

Для многих реальных систем отклонение от закона Рауля на столько значительно, что приводит к качественно новому состоянию системы, а на фазовых диаграммах П - x,у и t - х,у появляются (рисунок 6. III, IV) относительный максимум или минимум. В точке экстремума (т.А на рисунке 6. III,IV) кривые жидкой паровой фаз соприкасаются и составы равновесных фаз совпадают (х_А=у_А). Такие смеси называются азеотропными или нераздельно кипящими, т.к. при испарении смесь (азеотроп) не изменяет своего состава. Для разделения азеотропных смесей необходимы специальные методы (изменение давления, ректификация в присутствии третьего компонента и др.).

Эта особенность азеотропных смесей отражена о втором законе Коновалова: если давление и температура сосуществования двух бинарных фаз имеет экстремум (максимум или минимум), то составы фаз одинаковы.

Примером азеотропа на рисунке 6. , III может служить смесь сероуглерод-ацетон при П=87кПа. Температура азеотропа t_A=35^oC; состав (по сероуглероду) (температура кипения сероуглерода около 46^оС; ацетона - 56^оС).

Примером азеотропа на рисунке 6. ,IV можно назвать смесь ацетон – хлороформ при П=0,1МПа. Температура кипения азеотропа

Понятие перегонки. Схема установки.

Перегонкой называется процесс разделения гомогенных смесей компонентов, отличающихся температурами кипения, за счет переноса компонента из жидкой фазы в паровую ( или наоборот) при отсутствии противотока этих фаз.

Под простой перегонкой (или дистилляцией) понимают процесс однократного частичного испарения исходной жидкой смеси и конденсации образующихся при этом паров. Сконденсированные пары называют дистилляторам (Д), а оставшуюся не испаренной жидкость – остатком (W).

Перегонку применяют для предварительного разделения смесей компонентов, очистки веществ от примесей, смол, загрязнений,

Процесс перегонки можно проводить периодически либо непрерывно. Принципиальная схема периодической перегонки приведена на рисунке 6.1а.

Исходная смесь загружается в куб 1, снабженный змеевиком, в которой подается чаще всего насыщенный водяной пар. Образующиеся пары конденсируются в конденсаторе- холодильнике 2; дистиллят отводится в сборник. При этом содержание низкокипящего компонента в кубовой жидкости уменьшается, что приводит к снижению содержания НКК в дистилляте – в начале процесса концентрация НКК максимальная, в конце – минимальная. После окончания процесса перегонки. жидкий остаток сливают из куба 1 и вновь загружают в него исходную смесь.

С целью получения фракций (или дистиллята разного состава) используют фракционную (или дробную) перегонку.

Процесс перегонки удобно анализировать по изобарной диаграмме (рисунок 6.2).

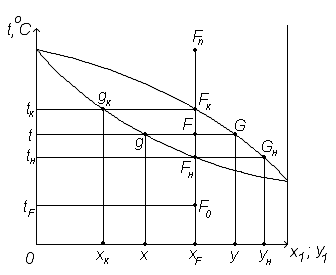
Предположим, что на перегонку поступает бинарная жидкая смесь при температуре t_F с концентрацией НКК x_F. Фигуративная точка, изображающая исходную смесь, обозначена т.F₀. При нагревании исходной смеси фигутативная точка F₀ на диаграмме t- x,y перемещается вверх, так как состав остается неизменным. Когда т.F₀ достигает линии кипения (т. F_н), жидкость состава ОС_F закипает ( t_н – температура начала кипения). При этом образуется паровая фаза с максимальной концентрацией НКК (Y_н). При дальнейшем повышении температуры (до значения t ) образуется равновесная парожидкостная система: паровая фаза (т.G) с концентрацией НКК y и жидкая (т. g ) с концентрацией НКК x. Состав этих равновесных фаз отличается от состава исходной смеси (X_F): в парах содержится больше НКК (y>X_F); в жидкости – больше ВКК (X<X_F). При дальнейшем повышении температуры (до значения t_к) т.F перемещается на линию конденсацию (т.F_к). Температура t_к есть температура конца кипения жидкости состава X_F. При этом выкипают последние капли жидкости (g_к), максимально обогащение ВКК (X_к). При дальнейшем нагреве (т.F_n) смесь представляет перегретый пар, состав которого равен составу исходной жидкости (y_n=x_F).

Таким образом, для разделения жидкой смеси состава x_F процесс перегонки необходимо проводить при t_н<t<t_k. При этом y_н – максимально возможная концентрация НКК в паровой фазе, а x_k – минимально возможная концентрация НКК в жидкой фазе.

Степень разделения компонентов в условиях перегонки может быть повышена применением дефлегмации.

На установке с дефлегмацией (рисунок 6.1 б) пары из куба 1 поступают в дефлегматор 4, где они частично конденсируется преимущественно ВКК, а пар обогащается НКК. Полученный в дефлегматоре конденсат (или флегма) в куб 1 и подвергается многократному испарению.

Материальный и тепловой балансы перегонки.

Уравнение материального и теплового балансов составили для непрерывного процесса перегонки.

Введем обозначения.

F,D,W – массовый расход соответственно исходной смеси (сырья), дистиллята и остатка, кг/ч;

x_F; y=x_D; x_w – концентрация НКК соответственно в сырье, дистилляте и остатке( масс.д.);

h_F; H; h_W – удельная энтальпия соответственно сырья, парового потока, выходящего из куба, и остатка;WF

Q_В – количество теплоты, выделяющейся при конденсации греющего пара в змеевике.

Материальный баланс можно записать

- по внешним потокам

F=D+W (6.44)

- по низкокипящему компоненту

Fx_F=Dx_D+Wx_W (6.45)

Решение системы уравнений (6.44) и (6.45) позволяет определить выход дистиллята и остатка

(6.46)

Тепловой баланс для куба имеет (без учета потерь тепла в окружающую среду)

Q_F+Q_B=Q_n+Q_W (6.47)

где Q_F – приход теплоты с сырьем;

Q_n – расход теплоты с уходящим из аппарата паровым потоком;

Q_W – расход теплоты с остатком или с учетом принятых ранее обозначений

(6.48)

из которого расход теплоты на проведение процесса перегонки определяется следующим образом (кВт)

(6.49)

Расход греющего пара в змеевике (кг/с)

(6.50)

где r – удельная теплота конденсации греющего пара, кДж/кг.

Перегонка с водяным паром

Для разделения нерастворимых в воде жидких смесей используется перегонка с «острым» водяным паром. При этом температура кипения смеси ниже температуры кипения чистых компонентов и является постоянной независимо от состава жидкой смеси, пока в жидкости присутствуют хотя бы следы второго компонента.

Расход острого пара на 1кг перегоняемого i-го компонента сырья из уравнения (6.

(6.51)

В действительности расход острого пара больше, поскольку уходящее из перегонного аппарата водяные пары не насыщаются полностью парами отгоняемого компонента, кроме того, уравнение (6.51) не учитывает расход пара на нагрев и испарение сырья. Поэтому перегонка с водяным паром целесообразна только в случае обязательного выделения из относительно нелетучей среды летучих компонентов, не смешивающихся с водой при нормальной температуры.

Для n-компонентной системы уравнение (6.33) запишется

или (6.35)

которое называется уравнением изотермы жидкой фазы многокомпонентной равновесной системы.

Уравнение изотермы паровой фазы бинарной равновесной системы выводится аналогично

или (6.36)

Для n-компонентной системы уравнение изотермы паровой фазы имеет вид

(6.37)

Уравнение изотермы бинарной системы (уравнения 6.34 и 6.36) и многокомпонентной (уравнения 6.35 и 6.37) позволяют определить температуру системы по известному давлению либо давление по заданному значению температуры