
Разработка детерминированныхматематических моделей химико-технологических процессов
.pdf
Недостатками рассмотренного решения задачи являются:
- совпадение значения В=Вmax при различных шагах интегрирования может быть формальным (случайным) и полная гарантия правильности расчета кинетики обеспечивается лишь при совпадении кинетических кривых при различных шагах интегрирования ∆τ;
-решение не позволяет рассмотреть кинетику решения задачи в целом, ибо значения концентраций компонентов не выводится на печать или дисплей.
Очевидно, что для устранения этих связанных с друг другом недостатков необходимо результаты расчета выводить на печать и сравнивать между собой при различных значениях шага интегрирования. Чтобы избежать операций с чрезмерным объемом информации (например при шаге интегрирования 0,0001 и τр=1 придется проанализировать до 30000 значений концентраций компонентов А, В и С при каждой вариации шага интегрирования ∆τ), будем подвергать анализу значения концентраций компонентов А, В и Столько в реперных точках, сканирующих область исследования с большим шагом ∆τrep>>∆τ. При этом дробление шага интегрирования ∆τ в ходе поиска правильного решения следует брать таким, чтобы ∆τrep всегда укладывалось в целое число ∆τ. Достаточно взять 5-10 реперных точек для достаточно полной информации о кинетики и, например, при τр=1 мы будем анализировать 15÷30 значений концентраций компонентов А, В и С вместо 30000 значений.
Для обеспечения вывода информации только в реперной точке, когда фактическое время реакции совпадает с позицией реперной точки, можно воспользоваться двумя приемами:
а) если продолжительность реакции примерно известна, то приняв ∆τrep, можно сделать следующую вставку между блоками 4 и 5; во вставке j – время по оси реперных точек:
|
4 |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
j=0, τp, ∆τrep |
|
|
|
5 |
||
|
|
|
|||||
Нет |
|
|
Да |
||||
|
|
||||||
j=τ+∆τ |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
A1, B1, C1, j |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
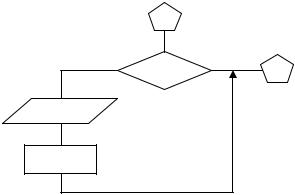
б) если τр неизвестна, то вставка между блоками 4 и 5 примет вид:
|
4 |
|
|
Да |
j=τ+∆τ |
Нет |
5 |
|
|
A1, B1, C1, j
j=j+∆τrep
Для получения правильного решения необходимо сформировать и сохранить в памяти массивы значений концентраций A(i), B(i), C(i), выводимых в i-тых реперных точках при шаге ∆τ, и также сохранить в памяти предыдущие массивы концентраций A0(i), B0(i), C0(i), полученный ранее при большем ∆τ.
Массивы A0(i), B0(i), C0(i) следует ввести число исходных данных. Значения A0(i), B0(i), C0(i) могут быть произвольными, например, равными 0, так как после первоначального решения задачи с шагом ∆τ и получением массива значений концентраций A(i), B(i), C(i) в реперных точках и естественного несовпадения значений элементов A0(i) и A(i), B0(i) и B(i), C0(i) и C(i) выполняется переадресовка массивов и дробление шага интегрирования аналогично блоксхеме на рисунке 5 до тех пор, пока кинетические кривые, рассчитанные с различными шагами интегрирования, не совпадут с заданной погрешностью расчета Е (например, Е=0,01A(i)) для всех реперных точек по каждому компоненту. В результате решения задачи на экран выведутся достаточно достоверные значения A(i), B(i), C(i) в реперных точках, оптимальное время τопт и максимальный выход компонента В=Вmax.
Если число реперных точек взято с избытком, то после достижения максимальной концентрации компонента В остальные дальнейшие реперные точки сохраняют нулевое значение и в анализе не участвуют [1].
Начало
CA0, CB0, CC0, ∆τ, k1, k2, k3, N
i=1, N |
A0(i)=0, B0(i)=0, |
C0(i)=0 |
τ=0, i=0, j=∆τrep
A=CA0, A(i)=A,
B=CB0, B(i)=B,
C=CC0, C(i)=C
A1=A-k1∙A∙∆τ,
B1=B+(k1∙A-k2∙B+k3∙C2)∙∆τ,
C1=C+(k2∙B-k3∙C2)∙∆τ
|
|
Нет |
|
|
|
|
Да |
|
|||
|
j=τ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
A=A1, |
|
|
|
|
|
|
|
|
|
||
B=B1, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i=i+1, A(i)=A, |
||||||
C=C1, |
|
|
|
|
|
||||||
|
|
|
|
|
B(i)=B,C(i)=C, |
||||||
τ=τ+∆τ |
|
|
|
|
|
||||||
|
|
|
|
|
j=j+∆τrep |
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Да |
|
|
|
|
Нет |
||||
B1>B |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
i=1, N |
|
|
|
|A0(i)-A(i)| |
Нет |
|
|
|
|
|
|
<0.01A(i) |
|
|
|
Да |
|
|
|
|B0(i)-B(i)| |
Нет |
|
|
|
|
|
|
<0.01B(i) |
|
|
|
Да |
|
|
|
|C0(i)-C(i)| |
Нет |
|
|
|
|
|
Да |
<0.01C(i) |
|
|
|
|
|
|
|
∆τ=∆τ/2 |
|
|
|
i=1, N |
|
τопт=τ, |
A0(i)=A(i), |
|
|
Bmax=B |
B0(i)=B(i), C0(i)=C(i) |
||
|
|
|
|
|
|
j=∆τrep |
|
|
|
i=1, N |
|
A(i), B(i), C(i),j
j=j+∆τrep
τопт, Bmax
Конец
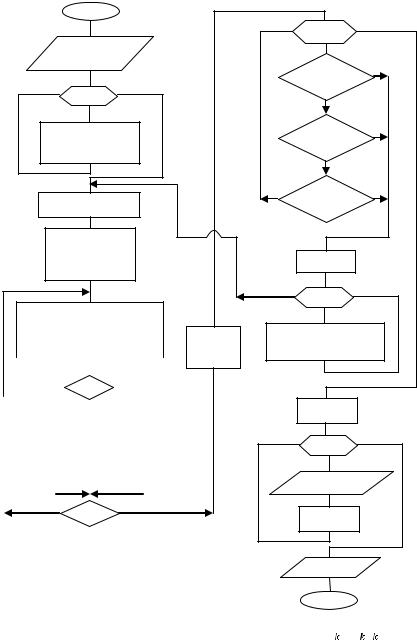
Рисунок 5 - Блок-схема расчета кинетики реакции 




 с автоматическим обеспечением правильности решения и выводом данных по кинетике реакции в реперных точках
с автоматическим обеспечением правильности решения и выводом данных по кинетике реакции в реперных точках
4 МОДЕЛИРОВАНИЕ РАБОТЫ ИЗОТЕРМИЧЕСКОГО РЕАКТОРА С ГИДРОДИНАМИКОЙ ИДЕАЛЬНОГО ВЫТЕСНЕНИЯ
Рассмотрим принципы разработки полной модели реактора, в котором
протекает последовательная реакция 




 , частные реакции 1 и 2 имеют первый порядок, реакция 3 - второй порядок. k1, k2, k3 – константы скоростей частных реакций, целевой компонент – В, гидродинамика реактора описывается моделью идеального вытеснения. Цель моделирования – определение условий проведения реакции и размеров реактора (диаметр D и длина Xp), при которых выход целевого компонента реакции будет стремиться к максимальному. Полнота разрабатываемой модели определяется в ходе анализа решения задачи.
, частные реакции 1 и 2 имеют первый порядок, реакция 3 - второй порядок. k1, k2, k3 – константы скоростей частных реакций, целевой компонент – В, гидродинамика реактора описывается моделью идеального вытеснения. Цель моделирования – определение условий проведения реакции и размеров реактора (диаметр D и длина Xp), при которых выход целевого компонента реакции будет стремиться к максимальному. Полнота разрабатываемой модели определяется в ходе анализа решения задачи.
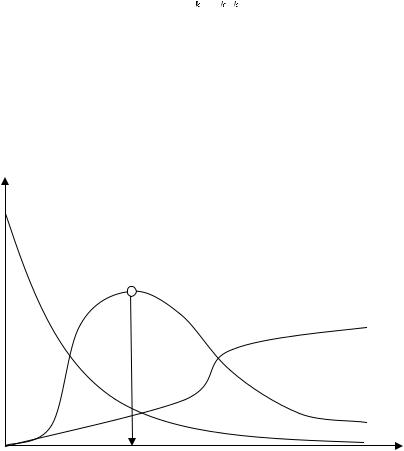
Необходимо разработать полную модель реактора в виде совокупности частных химической и гидродинамической моделей системы, позволяющей рассчитать профиль концентраций компонентов реакционной смеси по длине реактора (рисунок 6).
Сi
CB max
СC
|
СB |
|
СА |
Хр |
Х |
|
|
Рисунок 6 – Распределение концентраций компонентов реакционной |
|
смеси СА, СВ, СС по длине реактора Хр |
|
Химическая модель – модель кинетики химической реакции представляет собой систему дифференциальных уравнений, описывающих изменение концентраций компонентов во времени процесса τ

Гидродинамическая модель процесса представляет систему дифференциальных уравнений гидродинамики идеального вытеснения, записанную для каждого из компонентов реакционной смеси
где W – линейная скорость реакционной смеси в реакторе.
Каждая из частных моделей характеризует изменение концентрации каждого из компонентов за счет конкретного явления – химизма процесса и особенностей гидродинамики аппарата независимо друг от друга.
Первый вариант полной модели изотермического реактора получаем суммированием химической и гидродинамической частных моделей, так как изменение концентраций каждого из компонентов реакционной смеси во времени в целом определяется, с одной стороны, скоростью химического процесса, а с другой – скоростью гидродинамического процесса, а когда скорость процесса определяется набором частных скоростей, то скорость процесса в целом находят суммированием частных скоростей.
Для рассмотренной реакции полная модель изотермического реактора имеет вид:
С позиций проектирования наиболее интересно исследование процесса при его стационарной реализации 

 , тогда
, тогда
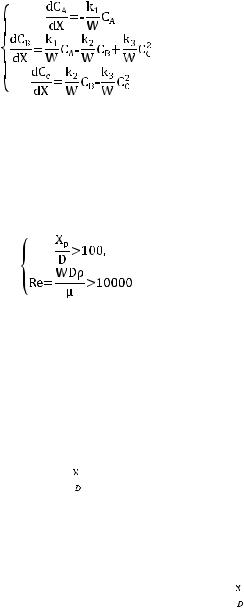
или
Полная модель реактора по форме совпадает с системой дифференциальных уравнений, описывающей кинетику химической реакции, поэтому принципы, используемые при разработке блок-схемы решения задачи кинетики (рисунок 5) подходят и для моделирования реактора в целом.
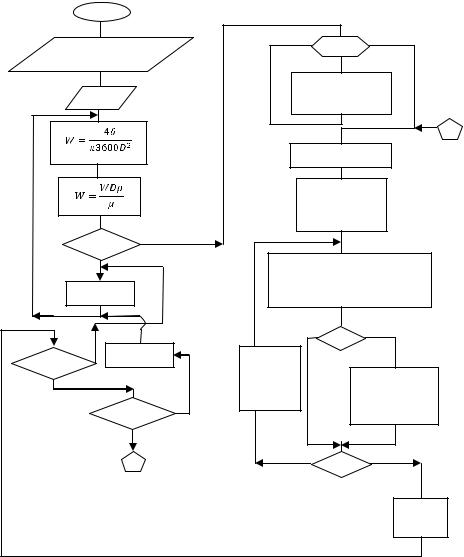
Дополнительной особенностью алгоритма расчета рассматриваемой задачи является неопределенность решения, так как скорость потока W зависит от диаметра D, причем необходимо обеспечить режим идеального вытеснения в рассчитанном аппарате, который гарантируется при соблюдении следующих условий:
где Re – число Рейнольдса,
ρ и μ – плотность и вязкость потока.
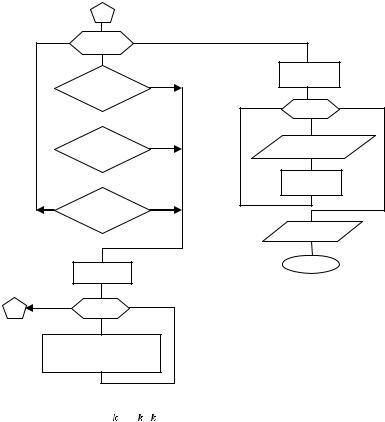
Очевидно, задачу приходится решать методом последовательных приближений. Принимая величину D, необходимо вначале рассчитать W, затем, рассчитывая профиль концентраций по длине реактора, определить оптимальную длину реактора Хопт, и если проверка на гарантию идеальности режима вытеснения не выдерживается, то изменить (уменьшить), например, на 0,01 м, величину D и повторить расчет. Так как при достаточно малом D (и большой скорости) режим вытеснения гарантируется, может возникнуть ситуация большого перепада давления в реакторе, которое исключается путем ввода дополнительного ограничения


 ,
,
которое не позволит проектировать аппарат с чрезмерным перепадом давления. Блок-схема решения примера дана на рисунке 7. В алгоритме решения
учтено также автоматическое обеспечение правильности расчета как с учетом выбора приемлемого шага интегрирования ∆Х, так и с учетом ограничений на гарантию режима идеального вытеснения и недопущения чрезмерных перепадов давления, при этом предварительный выбор диаметра D выполняется на основе
числа Рейнольдса, а окончательный – на основе ограничений 



 .
.
После проведения Хр выполняется уточнение расчета распределения концентраций компонентов А, В, и С по длине реактора с последовательно уменьшающимися шагами интегрирования до достижения приемлемой точности расчета (значения концентраций в сходственных точках для разных вариантов
значений шагов интегрирования имеют приемлемые незначительные расхождения).
Итоговое решение выводится как оптимальная точка расчета длины змеевика с выводом распределения концентраций компонентов А, В и С, в реперных точках по длине змеевика с гарантией правильности расчета во всех промежуточных точках в пределах допустимой точности расчета – 1% от величины рассчитываемой концентрации по любому компоненту [1].
Начало |
|
|
|
|
CA0, CB0, CC0, ∆х, k1, k2, k3, |
|
i=1, N |
|
|
N, ∆хrep, μ, ρ, ϑ |
|
|
|
|
|
|
A0(i)=0, B0(i)=0, |
||
D=? |
|
C0(i)=0 |
|
|
|
|
|
|
2 |
|
|
x=0, i=0, j=∆xrep |
||
|
|
A=CA0, A(i)=A, |
||
|
|
B=CB0, B(i)=B, |
||
|
|
C=CC0, C(i)=C |
||
Re>10000 |
Да |
|
|
|
|
|
|
|
|
Нет |
|
A1=A-k1∙A∙∆x/W, |
|
|
|
|
B1=B+(k1∙A-k2∙B+k3∙C2)∙∆x/W, |
||
D=D-0.01 |
|
C1=C+(k2∙B-k3∙C2)∙∆x/W |
||
|
|
Нет |
j=x |
Да |
Нет |
|
|
|
|
|
|
|
|
|
D=D+0.01 |
A=A1, |
|
|
|
Xопт/D>100 |
|
|
|
|
|
B=B1, |
|
|
|
|
|
|
i=i+1, A(i)=A, |
|
Да |
|
C=C1, |
|
|
|
|
B(i)=B,C(i)=C, |
||
|
|
τ=τ+∆τ |
|
|
|
|
|
j=j+∆xrep |
|
Xопт/D<500 |
|
|
||
Нет |
|
|
||
|
|
|
|
|
Да |
|
|
|
|
|
1 |
Да |
B1>B |
|
|
|
Нет |
||
|
|
|
|
|
|
|
|
|
Xопт=x, |
|
|
|
|
Bmax=B |
1
i=1, N
|A0(i)-A(i)| Нет <0.01A(i)
Да 
Нет
|B0(i)-B(i)| <0.01B(i)
Да 
Нет
|C0(i)-C(i)| Да <0.01C(i)
|
∆x=∆x/2 |
2 |
i=1, N |
|
A0(i)=A(i), |
|
B0(i)=B(i), C0(i)=C(i) |
j=∆τrep |
i=1, N |
A(i), B(i), C(i),j |
j=j+∆τrep |
xопт, Bmax |
Конец |
Рисунок 7– Блок –схема расчета изотермического реактора идеального вытеснения для реакции 




 .
.
5 МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОДНОФАЗНЫХ ПОТОКОВ
5.1 Методические указания по теоретической части
Основой математической модели любого химико-технологического процесса, в котором происходит перемещение вещества, является математическое описание структуры потоков.
Гидродинамика реальных потоков настолько сложна, что на основании теоретических положений уравнения в общем виде можно вывести только для однофазных потоков, причем решение их известно только для частных случаев. Поэтому при составлении математических описаний приходится использовать приближенное представление о структуре потоков, основанное на том, что структура движущейся технологической среды характеризуется степенью перемешивания частиц.
Известно, что время пребывания частиц потока в аппарате является непрерывной случайной величиной. Основной ее характеристикой служат функции распределения времени пребывания: дифференциальная и интегральная. По виду функции распределения с некоторым приближением можно судить о внутренней структуре потока.
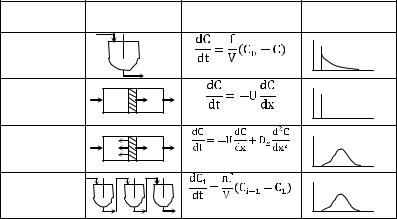
При разработке математической модели структуры потоков на практике прибегают к использованию так называемых типовых моделей. Наиболее распространенными из них являются: модель идеального перемешивания (МИП), модель идеального вытеснения (МИВ), ячеечная модель (ЯМ), однопараметрическая диффузионная модель (ОДМ) – табл. 1.
Таблица 1
Типовые |
Схема потока Математическое |
Отклик на |
модели |
описание |
имп.возмущ. |
МИП |
|
Cвых |
|
∞ |
t |
|
|
|
МИВ |
|
Cвых |
|
|
t |
ОДМ |
|
Cвых |
|
|
t |
ЯМ |
|
Cвых |
|
∞ ∞ ∞ |
|
|
|
t |
Модель идеального перемешивания предполагает, что поступающий в аппарат поток мгновенно распределяется по всему объему вследствие полного перемешивания. При этом концентрация вещества во всех точках аппарата и в выходном потоке одинакова.
Модель идеального вытеснения используется при описании аппаратов, работающих по принципу вытеснения. Трубчатые аппараты с большим отношением длины трубок L к диаметру d (L/d > 20) при турбулентном движении жидкости или газа могут описываться, как модели идеального вытеснения.
Однопараметрическая диффузионная модель предполагает, что поток движется в режиме идеального вытеснения, но в нем происходит продольное перемешивание.
Ячеечная модель основывается на том, что движущийся поток рассматривается состоящим из ряда последовательно соединенных ячеек. При этом принимается, что в каждой ячейке поток имеет структуру идеального перемешивания, а между ячейками перемешивание отсутствует.
Определение параметров МИП и МИВ не представляет особой трудности, так как сводится к расчетам коэффициентов дифференциальных уравнений по известным конструктивным и режимным параметрам.
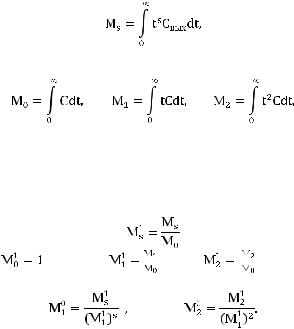
Рассмотрим идентификацию коэффициента продольного перемешивания Dx однопараметрической диффузионной модели. Функция распределения времени пребывания может быть охарактеризована числовыми характеристиками – моментами. Используются размерные моменты нулевого Мо, первого М1 и второго М2 порядков. Общая формула для нахождения размерных моментов:
где s – порядок момента, Свых – дифференциальная функция распределения времени пребывания. Тогда
Момент нулевого порядка равен площади, ограниченной кривой распределения. Момент первого порядка характеризует среднее время пребывания элемента потока в аппарате, момент второго порядка – дисперсии времени пребывания. От моментов для кривой отклика путем несложных преобразований можно перейти к приведенным моментам. Общая формула для приведенных моментов
тогда |
, |
|
|
|
. |
|
|
Безразмерные моменты вычисляем по формулам
Безразмерный момент второго порядка связан в свою очередь с параметрами ОДМ и ЯМ следующим образом:
