Мм_стохастические модели

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

филиал ФГБОУ ВПО УГНТУ в г. Стерлитамаке,

РАЗРАБОТКА СТОХАСТИЧЕСКИХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ

Учебно-методическое пособие по курсу «Моделирование в химической технологии и расчет реакторов»

Уфа 2012

Учебно-методическое пособие предназначено для студентов специальности 240401 «Химическая технология органических веществ» по курсу «Моделирование в химической технологии и расчет реакторов». В пособии рассмотрены теоретические вопросы, приведены методические указания для проведения лабораторных работ для раздела «Разработка стохастических математических моделей химико-технологических процессов». Даны рекомендации по выполнению лабораторных работ.

Составители: Пучкова Л.Н., старший преподаватель, канд. техн. наук Быковский Н.А., доц., канд. техн. наук Фанакова Н.Н., ассистент, канд. техн. наук

Рецензент Даминев Р.Р., проф., д-р техн. наук

© Уфимский государственный нефтяной технический университет, 2012

1 ПРАВИЛА ПО ТЕХНИКЕ БЕЗОПАСНОСТИ ЛАБОРАТОРИИ

Лабораторные стенды и вычислительная техника в лаборатории «Изме- рительно-вычислительный комплекс по моделирования химикотехнологических процессов и лабораторных стендов» питаются от источников электрической энергии с напряжением 220 В, поэтому при проведении работ необходимо строгое соблюдение правил по технике безопасности.

1 Нахождение посторонних лиц (в частности, студентов, свободных от выполнения работ) в лаборатории без ведома преподавателя, проводящего занятия, запрещается.

2 Приступать к выполнению лабораторного практикума можно только после изучения инструкций и инструктажа по технике безопасности на рабочем месте. При этом обязательно оформление контрольного листа по технике безопасности в соответствии с требованиями.

3 Перед началом работы студент обязан осмотреть и привести в порядок рабочее место, проверить правильность подключения ПК в электросеть, проверить исправность токоведущих проводов, вилок, розеток, повреждение изоляции проводов, сколы вилок и розеток не допускаются. Кабель или питающие провода ПК должны в обязательном порядке иметь заземляющий контакт.

4 При работе с ПК студент обязан выполнять ту работу, которая ему поручена руководителем и по которой он был проинструктирован, не загромождать оборудование посторонними предметами, документацией и т.п., которые снижают теплоотдачу.

5 Не оставлять включенный ПК без присмотра. По окончании работы студент должен сообщить об этом преподавателю, выключить ПК привести в порядок рабочее место.

2 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ

2.1 Порядок выполнения лабораторных работ

Перед началом лабораторной работы студент обязан познакомиться с инструкциями по технике безопасности, прослушать инструктаж по т/б на рабочем месте и расписаться в контрольном листе инструктажа по т/б.

Прежде чем приступить к выполнению лабораторной работы, необходимо изучить ее теоретическую часть, блок-схему и разработать план выполнения лабораторной работы.

После написания программы студент должен показать и ее преподавателю. Полученные данные записывать в соответствующие таблицы. Необходимые вычисления проводить аккуратно с точностью до третьей значащей цифры.

По окончании лабораторной работы показать преподавателю полученные результаты.

2.2 Правила оформления отчета

Приступать к оформлению отчета по лабораторной работе следует после выполнения всех экспериментов и необходимых математических расчетов. Отчет оформлять на стандартных листах формата А4 с соответствующими рамками и угловыми штампами согласно ЕСКД. Все рисунки, схемы, элементы электрических цепей, графики должны быть выполнены согласно ЕСКД с помощью чертежных инструментов. При выполнении графиков на осях координат указывать откладываемые величины и единицы их измерения.

На титульном листе отчета должны быть указаны наименование министерства, университета, филиала кафедры и самой лабораторной работы. Затем пишутся фамилия и инициалы студента, выполняющего работу, а также указывается его группа, а ниже – фамилия и инициалы преподавателя, проверяющего работу.

При оформлении лабораторной работы нужно указать все необходимые расчетные формулы. Вычисление проводятся до третьей значащей цифры. В конце отчета необходимо указать список используемой литературы. Для защиты отчета по лабораторной работе необходимо ответить на все контрольные вопросы.

2.3 Содержание отчета

Отчет по лабораторной работе должен содержать титульный лист, цель работы, приборы и принадлежности, химические реактивы, задание на работу, схему лабораторной установки, экспериментальные данные, расчетные формулы, графики, диаграммы и выводы.

ВЫБОР ВИДА И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЭМПИРИЧЕСКОЙ ЗАВИСИМОСТИ

Методические указания по теоретической части

Часто перед исследователем в любой области возникает следующая задача. Имеется объект исследования ОИ (рисунок 1), который характеризуется

набором переменных: входных – и выходной – . Требуется найти зависимость выходной переменной от входных.

Рисунок 1 - Схема объекта исследования

При этом считается, что механизмы процессов, протекающих внутри объекта исследования, неизвестны, а имеются только соответствующие значения входных и выходных параметров. Такая задача носит название задачи «черного ящика».

Рассмотрим простейший случай, когда на вход действует только одна переменная

Решение задачи моделирования в этом случае состоит из ряда этапов: 1 проведение эксперимента; 2 выбор вида эмпирической зависимости;

3 нахождение параметров выбранной зависимости;

4 исследование модели и выводы.

На первом этапе задаем значение входной переменной из возможного диапазона и замеряем соответствующие значения выходной переменной . Результат представляем в следующем виде:

…

…

По экспериментальным данным строим график (рисунок 2).

Рисунок 2 - Экспериментальная кривая

На втором этапе необходимо подобрать формулу, которая могла бы описать экспериментальные данные. В таблице 1 приведены основные типовые формулы, наиболее часто встречающиеся в задачах химии и химической технологии.

Для выбора вида зависимости воспользуемся методом средних точек. Для каждой зависимости рассчитываем координаты средних точек и по формулам из табл. 1.1. Средние точки наносим на график (рисунок 2) и выбираем ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой.

Таблица 1

3

4

5

6

На третьем этапе необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой. В качестве критерия близости выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями:

Тогда система нормальных уравнений для определения параметров линейной зависимости будет иметь вид:

где ; ; ; ;

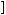
– количество экспериментов.

Решив эту систему, получаем искомые значения параметров.

Следует отметить, что при нахождении параметров других зависимостей необходимо сначала привести их к линейному виду согласно таблице 1.

На четвертом этапе получаем расчетные значения подстановкой в найденную формулу экспериментальных значений входной величины.

…

…

Полученные значения наносим на график с экспериментальными данными и делаем вывод об адекватности [1, 2].

Методические указания по практической части

В результате эксперимента получены следующие данные:

:

Рисунок 3 - Экспериментальная кривая

3);;

4); ;

5); ;

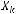
6); ;

Значения и для всех формул наносим на график. Точка 4 лежит ближе всего к экспериментальной кривой, следовательно, выбираем формулу

.

В линейном виде ,где. Система нормальных уравнений имеет вид:

Находим коэффициенты этой системы. Для этого оформляем таблицу 2.

Таблица 2

Решаем систему

,

.

Эти значения функции совпадают с экспериментальными, следовательно, исследуемый объект описывается уравнением

.

Блок-схема решения данной задачи на ЭВМ приведена на рисунке 4.

СТАТИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ

Методические указания по теоретической части

В последнее время для моделирования и оптимизации различных процессов широко применяются активного планирования эксперимента. С их помощью исследователь проводит эксперимент по заранее составленному плану при минимальных затратах на получение необходимых данных об изучаемом объекте и его оптимизацию. При этом сведения о механизмах процессов, протекающих внутри объекта, отсутствуют. Модель составляется по значениям входных и выходных переменных. При решении оптимальных задач к традиционным четырем этапам моделирования (проведение эксперимента, выбор вида модели, определение параметров модели, проверка адекватности) добавляется еще этап оптимизации. В активном эксперименте первые два этапа моделирования взаимосвязаны, т.е. план проведения эксперимента зависит от того, какая выбрана модель. Обычно математическая модель объекта в многофакторных задачах записывается в виде полинома некоторой степени (в зависимости от требуемой точности):

где - выходная переменная (целевая функция или параметр оптимиза-

ции);

– входные переменные или факторы ( ;

– число факторов.

Точные значения коэффициентов уравнения (5) определить невозможно, поэтому вместо истинных значений коэффициентов отыскиваются их оценки . Тогда уравнение (5) перепишется в виде:

Уравнение (6) называется уравнением регрессии, а коэффициенты – коэффициенты регрессии. При первоначальном исследовании объекта обычно применяют линейное уравнение регрессии:

Для расчета коэффициентов регрессии и минимизации количества опытов используется полный факторный эксперимент (ПФЭ), в ходе которого каждый фактор варьируется на определенном числе уровней. Для линейного