samoilov_n_a_modelirovanie_v_himicheskoi_tehnol

81

если в ходе анализа уравнения регрессии часть его коэффициентов будет признана незначимой.

3.2. Основы теории активного эксперимента

При выполнении активного эксперимента опыты ставятся по заранее разработанной программе, обладающей рядом специфических свойств и называемой матрицей планирования. При этом число опытов зависит от вида матрицы и является жестко фиксируемым. Различные виды матриц планирования позволяют получать различные формы уравнения регрессии.

Матрицы планирования первого порядка

Эти матрицы обеспечивают разработку уравнений регрессии первого порядка. Одним из вариантов решения задачи является полный факторный эксперимент. Минимизация объема эксперимента при этом требует проведения опытов при двух значениях каждого из параметров (факторов) процесса Х, поэтому число проводимых опытов N составляет

где К – число независимых параметров в моделируемом процессе.

В этом случае уравнение регрессии, включающее линейные члены и эффекты взаимодействия, насчитывает столько же коэффициентов, сколько опытов включено в матрицу планирования. Например, для трех

факторов X1 , X2 , X3 N 8 и уравнение регрессии представляет собой восьмичленный полином, включающий эффекты парного и тройного взаимодействия факторов процесса

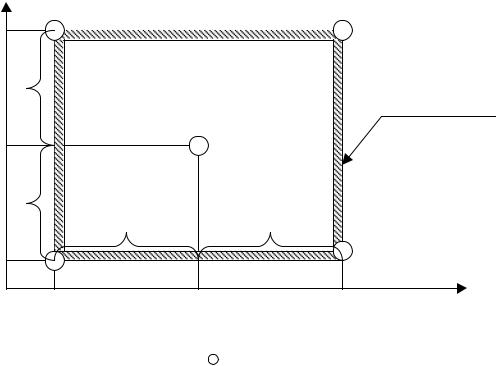
Координаты экспериментальных точек в матрице планирования не произвольны. Опыты ставятся только в вершинах области исследования, в которых параметры эксперимента принимают только максимальное или минимальное значение. Поэтому для формирования области исследования предварительно необходимо выбрать диапазон варьирования каждого из параметров процесса в пределах X i , MAX X i , MIN . На рис 3.6 показана

область исследования для двух факторов X1 , X 2 , при этом число опытов равно четырем. Область исследования характеризуется точкой центра плана с координатами X 0j , рассчитываемыми как

Таблица 3.2 Матрица планирования полного факторного эксперимента в натуральном

масштабе значений факторов процесса для двух факторов

Y1,Y2,…,Yi,…,YM в табл. 3.2 – результат реализации исследования процесса по матрице планирования эксперимента , когда выполнение одного эксперимента дает несколько параметров выхода Yi . Например, при исследовании процесса платформинга бензиновой фракции в качестве

83

независимых факторов X1 , X 2 приняты температура и давление процесса , а в качестве результатов исследования Yi нас могут интересовать: Y1 – выход катализата на сырье, Y2 – суммарное содержание ароматических углеводородов в катализате, Y3 : содержание бензола в катализате и т.д.

Очевидно, что эксперимент, поставленный по матрице планирования, приведенной в табл. 3.2., может в итоге дать систему уравнений регрессии в натуральных переменных, представляющую собой стохастическую модель процесса:

Коэффициенты уравнений регрессии в натуральных переменных могут быть вычислены методом наименьших квадратов, однако, в силу трудоемкости их расчетов, переходят вначале при обработке экспериментальных данных к кодированию переменных (факторов), представлению матрицы планирования в кодированной форме и к разработке уравнения регрессии в кодированной форме факторов.

При кодировании факторов любому натуральному (фактическому)

значению параметров процесса X j ставится в соответствие его

области исследования, где располагаются экспериментальные точки, они

Обычно матрица планирования в натуральных переменных дополняется фрагментом с кодированной частью, которая включает в себя

не только кодированные переменные x j , но и эффекты взаимодействия, а

также столбец фиктивного параметра xo с целью унификации уравнения регрессии, чтобы каждому коэффициенту уравнения регрессии соответствовал свой параметр, тогда уравнения регрессии в кодированной

84

форме, эквивалентные системе уравнений регрессии в натуральных переменных (3.30) примут вид:

регрессии не искажало расчета результатов процесса Yi.

Обобщенная матрица планирования, включающая натуральную и кодированную части представлена в табл. 3.3.

Таблица 3.3 Матрица планирования полного факторного эксперимента с натуральной и

кодированной частями для исследования двухфакторного процесса

характерными свойствами:

контрольное свойство, позволяющее проверять правильность составления матрицы

вспомогательное свойство, облегчающее расчет коэффициентов уравнения регрессии

i 1

свойство ортогональности матрицы в кодированных переменных, ускоряющее расчет коэффициентов уравнения регрессии

85

согласно этому свойству, сумма произведения кодированных параметров

для любых двух различных столбцов матрицы равна нулю.

Основой расчета коэффициентов кодированного уравнения регрессии b является, как и в пассивном эксперименте, метод наименьших квадратов. Функция наименьших квадратов для рассматриваемого примера будет иметь вид

первые производные Ф / b 0 . Тогда сформировав уравнения первых производных

86

Благодаря свойству ортогональности кодированной матрицы все элементы левой части системы уравнений (3.38) кроме диагональных элементов равны нулю и в итоге система взаимосвязанных уравнений (3.38) сводится к группе из четырех независимых уравнений, каждое из которых включает в себя один искомый коэффициент уравнения регрессии в кодированных переменных:

i 1

справедливой для простого и быстрого расчета коэффициентов уравнения регрессии по матрице планирования полного факторного эксперимента для любого числа факторов.

Дополнительным положительным качеством уравнений регрессии, полученных по ортогональной матрице планирования эксперимента является независимость коэффициентов друг от друга. Поэтому, если в ходе дальнейшего исследования уравнения регрессии окажется, что часть коэффициентов уравнения является незначимой, то оставшиеся значимые коэффициенты пересчитывать нет необходимости.

При разработке матрицы планирования для большого числа исследуемых факторов, могут появиться формальные трудности в построении матрицы таким образом, чтобы не допускать повторения (дублирования) опытов в матрице. Эта задача легко решается одним из алгоритмов построения матриц планирования в полном факторном

эксперименте для M факторов:

87

1. Строим простейшую матрицу планирования в кодированной форме для числа факторов k 2 , при этом число опытов N 2k 4 ;

2.Построенную матрицу назовем образующей матрицей;

3.Переписываем образующую матрицу под ранее написанной без изменений, число опытов становится 2N ;

4.Вводим в матрицу столбец очередного параметра, тогда в матрице

можно будет учесть k k 1 3– на один фактор больше;

5. Столбец нового (k 1) параметра по высоте (по числу опытов) делится пополам и кодам этого параметра xk 1 присваивается значение +1 в верхней части столбца и –1 в нижней части.

6.Если по мере выполнения алгоритма выполнится условие k M , то матрица построена по линейным столбцам и она дополняется столбцами эффектов взаимодействия, если же данное условие не выполнено (k M ), то возвращаемся на второй пункт алгоритма

Схема выполнения алгоритма показана в табл. 3.4. при построении матрицы планирования для трех факторов.

Таблица 3.4

Построение матрицы планирования полного факторного эксперимента первого порядка для трех факторов

(по столбцам факторов)

Недостатком уравнения регрессии в кодированных переменных является необходимость предварительного кодирования натуральных переменных X , чтобы рассчитать величину моделируемого параметра Y . Однако, кодированное уравнение регрессии вида (3.31) легко перевести в натуральную форму (3.32), если в кодированном уравнении регрессии каждую кодированную величину заменить соответствующей формулой кодирования (3.31) и выполнить простейшие преобразования уравнения.

89

Х2 – содержание с ацетилацетилена в исходном сырье, %;

Х2 МАХ =28, Х2 MIN = 20;

Х3 – содержание уксусной кислоты в реакционной массе, %,

Х3 МАХ =18, Х3 MIN = 12.

Составлена матрица планирования в кодированной форме, по её условиям выполнены эксперименты, результаты опытов У – выход целевого продукта, %, также введены в матрицу (табл. 3.5).

Число опытов N= 23 = 8.

В связи с тем, что уравнение регрессии будет описывать медленно протекающий процесс получения лекарственного препарата, для повышения уровня надежности уравнения регрессии все опыты повторялись и рассчитывался средний выход сульфадимезина по результатам двух параллельных опытов.

Разрабатываемое уравнение регрессии имеет в общем случае следующую кодированную форму:

Ў= aо + a1х1 + a2х2+ a3х3 + a12х1х2 + a23х2х3 + a13х1х3 + a123х1х2х3 , (3.47)

где ai – коэффициенты кодированного уравнения регрессии (таким образом, мы видим что формальные обозначения коэффициентов

уравнения регрессии не обязательно обозначать b , можно использовать любые буквенные обозначения.

Уравнение (3.47) учитывает как влияние самих исследуемых параметров на результат процесса У, так и влияние на У возможных эффектов взаимодействия (как парных эффектов, так и тройного эффекта).