samoilov_n_a_modelirovanie_v_himicheskoi_tehnol

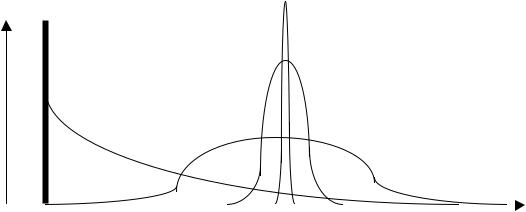
31

Математическое описание гидродинамики ячеечной модели имеет состоит из m уравнений вида

функции отклика диффузионной модели и зависит от числа ячеек (рис.

1.18).

m =2

Рис. 1.18. Формы функций отклика ячеечной модели при различном числе ячеек идеального смешения m

(сплошные линии) на импульсное возмущение (пунктирная линия)

При большом числе ячеек смешения ячеечная модель гидродинамики сближается с моделью идеального вытеснения. Число ячеек m является основным параметром ячеечной модели.

Функция отклика C( ) f ( ) при импульсном возмущении может быть рассчитана по уравнению

Если число ячеек m неизвестно, то оно может быть определено по дисперсии экспериментальной функции отклика:

32

Ячеечной моделью хорошо описывается гидродинамика тарельчатых ректификационных и абсорбционных колонн, секционированных аппаратов с псевдоожиженным слоем катализатора или адсорбента, каскады реакторов с мешалками, секционированные ферментеры.

Комбинированные гидродинамические модели

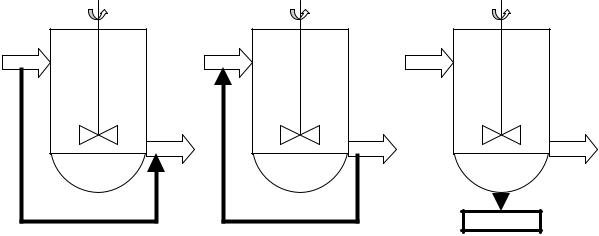
Хотя рассмотренные четыре класса гидродинамических моделей охватывают особенности гидродинамики практически всех основных аппаратов химической технологии, возможны сложные гидродинамические ситуации, когда ни одна из рассмотренных типовых моделей гидродинамики не может адекватно описать реальную структуру потоков. В этом случае используют комбинированные гидродинамические модели, представляющие собой структурную схему, состоящую из нескольких типовых гидродинамических моделей, связанных между собой в соответствии со спецификой реальной гидродинамики. При необходимости структурная схема может дополняться структурными элементами: байпасом, циркуляцией, застойной зоной. На рис. 1.19 представлены варианты комбинированных схем, состоящие из модели идеального смешения и одного из рассмотренных структурных элементов.

Рис. 1.19. Схемы структурных элементов комбинированных моделей

Байпас характеризуется проскоком части основного потока в аппарате без участия в процессе с временем пребывания в зоне байпаса условно равным нулю (условие неучастия байпасирующего потока, например, в химическом процессе). Циркуляция = это обратный заброс части технологического потока с конца процессе на его начало с временем пребывания в зоне прохождения циркулирующего потока условно равным

33

нулю. Застойная зона – часть объема аппарата с полным или частичным отсутствием взаимодействия с основным потоком.

В случае многофазных систем гидродинамические модели формируются по каждой из фаз отдельно.

Комбинированная гидродинамическая модель аппарата может быть сформирована на базе логического анализа возможной структуры потоков в аппарате или на основе анализа функции отклика на возмущение при экспериментальной оценке структуры потоков.

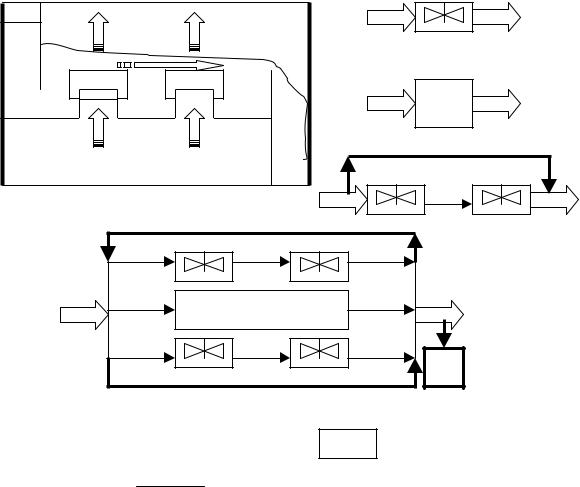
При логическом анализе структуры потоков один и тот же по конструкции аппарат может быть описан различными гидродинамическими моделями. Например, структура потоков жидкой фазы, протекающей по колпачковой тарелке ректификационной колонны может быть описана моделью идеального смешения, идеального вытеснения ячеечной моделью и рядом комбинированных моделей (рис.

1.20).

б

в

а

г

д

Рис. 1.20. Схема колпачковой ректификационной тарелки (а) и варианты структуры потоков по жидкой фазе ( – элемент идеального смешения, – элемент идеального вытеснения)(б-д)

Рассмотренное многообразие гидродинамических моделей колпачковой тарелки ректификациооной колонны не является произвольным или противоречивым, оно определяется конструктивными и

34

технологическими особенностями ректификационной колонны. Так, например, при малотоннажном разделении продуктов процессов тонкой химической технологии диаметр колонны может составлять 0.2-0.3 м, при этом на полотне тарелки размещается всего 1-3 колпачка и такой комплекс рядом расположенных барботажных перемешивающих устройств вполне с позиций гидродинамики может описываться моделью идеального смешения (рис.1. 20,б). В крупнотоннажных технологических процессах диаметр колонн может достигать 6-10 м (например, на установках АВТ), при этом по ходу потока жидкой фазы на тарелке размещается несколько десятков колпачков и такая система (см. стр. 31) с позиций гидродинамики может быть описана моделью идеального вытеснения (рис. 1.20,в). В колоннах среднего диаметра (1-3 м) уместно использование ячеечной модели. Если учесть, что вблизи стенки колонны часть потока может пройти вне зоны интенсивного барботажа и не будет контактировать с потоком пара, то ячеечная модель может быть дополнена байпасным структурным элементом, формируя комбинированную гидродинамическую модель (рис. 1.20,г). Детальный анализ работы колпачковой тарелки большого диаметра позволяет разработать более сложную комбинированную гидродинамическую модель (рис. 1.20,д), которая кроме модели идеального вытеснения, характеризующей гидродинамику центральной части потока будет включать ячеечные модели, характеризующей гидродинамику периферийной части потока, контактирующей с меньшим числом колпачков, а также будет учитывать байпасный структурный элемент, эквивалентный пристенной гидродинамике, циркуляционный структурный элемент, рассматривающий возможный заброс продукта с последующих по ходу потока колпачков на предыдущие и застойную зону вблизи переливной перегородки тарелки.

При экспериментальной оценке структуры потоков на основе анализа сложной функции отклика аппарата на возмущение, когда ее нельзя отождествить с функциями отклика известных типовых гидродинамических моделей, формирование комбинированной гидродинамической модели выполняется в три этапа:

декомпозиция экспериментальной функции отклика на простейшие составляющие части, соответствующие типовым гидродинамическим моделям;

формирование ряда комбинированных гидродинамических моделей на основе полученного на первом этапе набора вычлененных типовых гидродинамических моделей;

синтез качественных функций отклика для разработанных вариантов комбинированных моделей и сопоставление их с экспериментальной функцией отклика, что позволяет отобрать одну или несколько комбинированных моделей, адекватных в принципе гидродинамике реального аппарата.

35

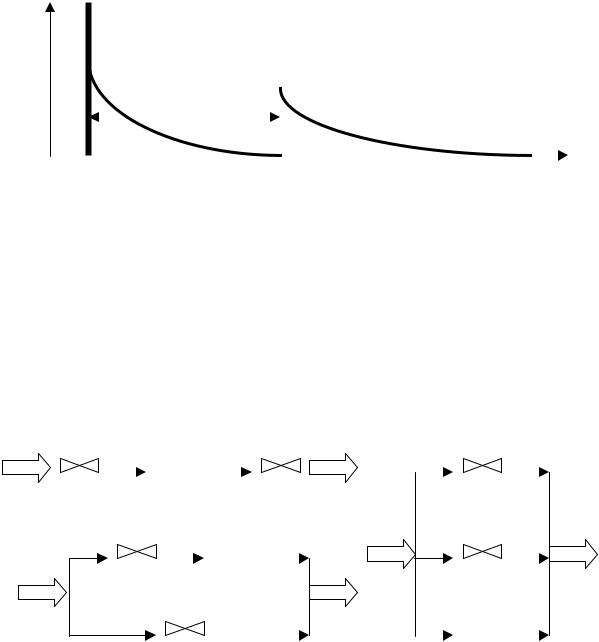
Рассмотрим решение этой задачи на примере. Пусть в ходе экспериментального исследования гидродинамики аппарата методом импульсного возмущения получена функция отклика C( ) f ( ), приведенная на рис. 1.21.

C( )

Рис.1.21. Экспериментальная функция отклика аппарата (сплошная линия) на импульсное возмущение (пунктирная линия)

Экспериментальная функция отклика в целом не соответствует ни одной из ранее рассмотренных типовых гидродинамических моделей, однако ее можно разложить на три фрагмента, эквивалентных типовым гидродинамическим моделям: две модели идеального смешения МИС1 и МИС2 и модель идеального вытеснения МИВ. Сочетание этих моделей позволяет сформировать ряд комбинированных гидродинамических моделей (рис. 1.22).

Рис. 1.22. Варианты комбинированных гидродинамических моделей, полученных из трех элементов: двух МИС и МИВ

а – последовательное соединение элементов; б – две параллельные ветви элементов; в – три параллельные ветви элементов

36

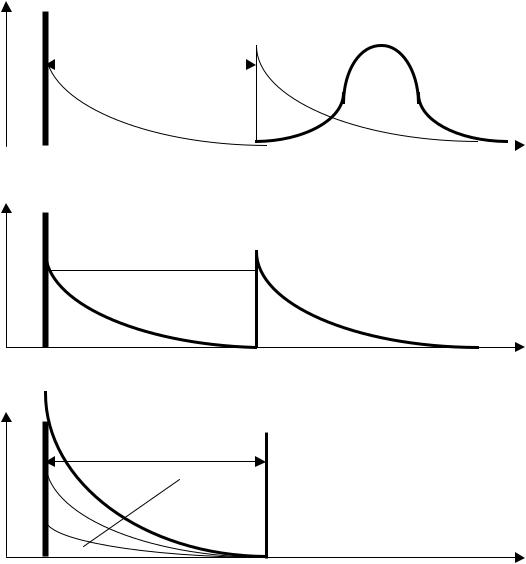
Синтез функции отклика комбинированной модели, полученной последовательным соединением моделей МИС1 , МИВ и МИС2 приводит к тому, что функция отклика МИС1 смещается моделью МИВ на время пребывания Т и становится в свою очередь возмущением для МИВ2, в итоге на выходе комбинированной модели получаем функцию отклика C( ) f ( ), соответствующую ячеечной модели (ЯМ), состоящей из двух ячеек идеального смешения, смещенную на время Т относительно времени ввода возмущения (рис. 1.23,а).

C( )

МИВ

C( )

МИВ

Т

ТМИВ

МИС1 МИС2

Рис.1.23 Синтезированные функции отклика для вариантов комбинированных гидродинамических моделей (рис.1.22), полученных из трех элементов: двух МИС и МИВ: а – последовательное соединение элементов; б – две параллельные ветви элементов; в – три параллельные ветви элементов

37

Синтез функции отклика комбинированной модели, полученной системой из двух параллельных ветвей приводит к тому, что в верхней ветви функция отклика МИС2 смещается моделью МИВ на время пребывания Т , функция отклика МИС1 формируется самостоятельно и после сложения функций отклика по концентрациям трассера для двух ветвей в итоге на выходе комбинированной модели получаем функцию отклика C( ) f ( ) (рис. 1.23,б), качественно похожую на экспериментальную функцию отклика (рис. 1.21). Синтез функции отклика комбинированной модели, полученной системой из трех параллельных ветвей приводит к тому, что функции отклика всех частных моделей формируется самостоятельно и после сложения функций отклика по концентрациям трассера для трех ветвей в итоге на выходе комбинированной модели получаем функцию отклика (рис.1.23,в), которая существенно отличается от экспериментальной.

Таким образом, из трех рассмотренных вариантов комбинированной гидродинамической модели экспериментальной функции отклика принципиально соответствует лишь вариант с двумя параллельными ветвями структурной гидродинамической схемы (рис. 1.22,б).

1.3.3. Расчет параметров гидродинамических моделей

Практическое использование гидродинамических моделей в процессе математического моделирования химико-технологических систем возможно только тогда, когда известны численные значения параметров гидродинамических моделей. К таким параметрам относятся для модели идеального смешения – среднее время пребывания продукта в аппарате Т, для модели идеального вытеснения - время Т, для

смешения m. Эти параметры можно вычислить в ходе обработки экспериментальной функции отклика аппарата на импульсное возмущение при помощи статистических моментов.

В теории вероятности статистические моменты позволяют получать ряд характеристик функций распределения случайной величины. Функцию отклика C( ) f ( ) также можно интерпретировать как функцию распределения случайной величины. Различают начальные и центральные статистические моменты. Начальные статистические моменты рассчитывают по фактической функции распределения (функции отклика

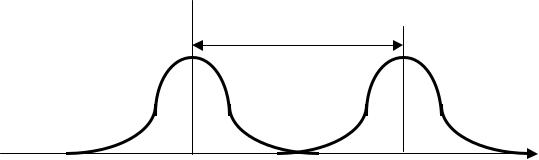
фактического расположения по оси на величину математического ожидания среднего времени пребывания потока в аппарате М (рис. 1.24).

38

C( )

М

0

Рис. 1.24. К расчету начальных и центральных статистических моментов (М - математического ожидание среднего времени пребывания

потока в аппарате)

Различают ряд начальных и центральных статистических моментов, отличающихся по порядку моментов, в общем случае статистические моменты S-ого порядка рассчитываются по уравнениям для начальных моментов

а для центральных моментов

где М(1) – первый начальный статистический момент.

Из всего многообразия статистических моментов с позиций расчета параметров гидродинамических моделей наибольший интерес представляют нулевой и первый начальный моменты и второй центральный момент.

Нулевой начальный статистический момент

характеризует площадь под функцией отклика и эквивалентен (пропорционален в масштабе эксперимента) величине возмущения, например, количеству трассера, проходящего по соответствующей ветви комбинированной гидродинамической модели и, соответственно, количеству технологического потока, проходящего по этой ветви.

39

Первый начальный статистический момент

характеризует математическое ожидание среднего времени пребывания возмущения (трассера) и, следовательно, технологического потока в соответствующем элементе блок-схемы комбинированной модели.

Второй центральный статистический момент

характеризует специфические отклонения гидродинамики соответствующего элемента блок-схемы комбинированной гидродинамической модели от гидродинамики модели идеального вытеснения и позволяет рассчитать основной параметр этого элемента, например, для диффузионной модели критерий Пекле Ре рассчитывается

по уравнению

при Ре>10 или исходя из уравнения

при Ре<10,

а число ячеек ячеечной модели m находят из условия

В связи с тем, что в теории вероятности величина нулевого начального статистического момента равна 1 , а величина возмущения в эксперименте (например, количество трассера, введенного в ходе исследования гидродинамики) является достаточно произвольной величиной, уравнения (1.31) – (1.32) нормируют, разделив их на уравнение (1.30), при этом устраняется влияние количества введенного трассера на статистические моменты первого и второго порядков и они становятся величинами, не зависящими от условий проведения эксперимента, тогда

40

C( )d

При проведении расчетов статистических моментов для фрагментов декомпозируемой функции отклика необходимо пределы интегрирования (± )привести в соответствие с реальными условиями прохождения возмущения через анализируемый фрагмент функции отклика (рисунок), при этом нижний предел интегрирования для каждого фрагмента должен быть равен нулю, то есть условному времени входа возмущения в фрагмент , а верхний – условному времени выхода возмущения из этого фрагмента функции отклика, так, чтобы продолжительность прохождения возмущения через элемент τ составляла

где τ(1) и τ(2) соответственно условное время входа и выхода возмущения из структурного элемента гидродинамической модели (фрагмента комбинированной модели) по отношению к времени начала эксперимента τ0 (время ввода импульсного возмущения).

Статистические моменты как интегралы рассчитывают по экспериментальной функции отклика обычно численными методами прямоугольников или трапеций.

В качестве примера рассмотрим результаты расчетов статистических моментов по функции отклика, снятой для аппарата со сферическими днищами диаметром 1.2 м и полной высотой 15 м объемом 16.5 м3 при прохождении через него технологического потока с расходом 50 м3/ч.

Формальное время пребывания потока в аппарате составляет 16.5/50=0.33 час или 19.8 мин. Однако это время не отражает специфики конструкции аппарата, его внутренних контактных устройств и реальной гидродинамики.

Корректный анализ работы аппарата можно выполнить лишь при исследовании структуры потоков в аппарате.