samoilov_n_a_modelirovanie_v_himicheskoi_tehnol

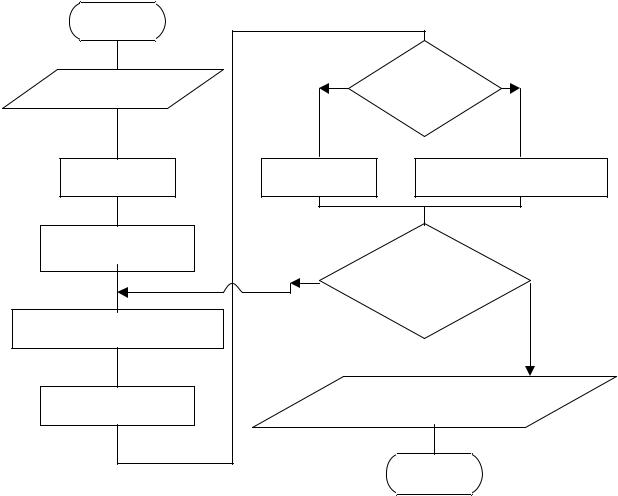
181

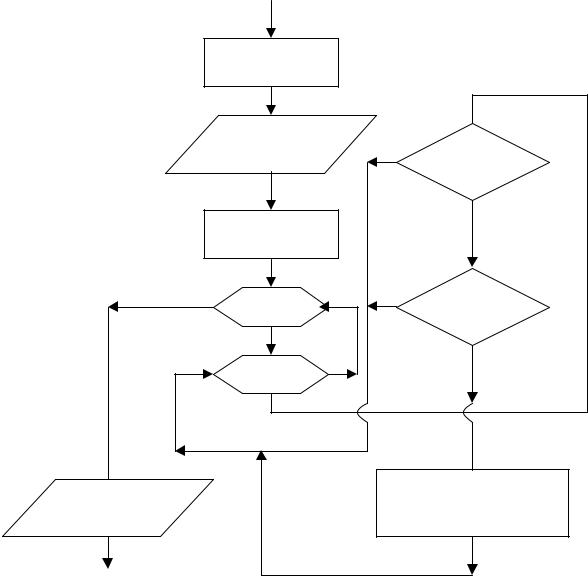
Блок схема расчета корней алгебраического уравнения методом половинного деления приведена на рис. 6.12. Метод гарантирует получение решения задачи с заданной точностью и имеет значительно лучшее быстродействие, чем метод сканирования, так, например, если Х – это температура процесса, исследуемая в интервале 100-400 0С с точностью поиска корня 0.5 0С, то для решения задачи будет необходимо выполнить 12 циклов расчета, тогда как при применении метода сканирования будет произведено 600 циклов расчета.

6.2.4.Алгоритмы работы с табличными материалами

Втехнологических расчетах часто применяется справочный табличный материал. В ходе формирования решения основной задачи бывает необходимо внести в программу справочную таблицу и извлечь из

182

нее необходимый параметр, который далее будет использоваться в расчетах.

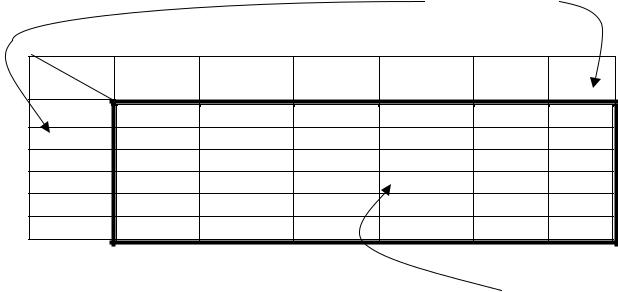
Таблица в общем случае (рис. 6.13) характеризуется телом таблицы, содержащим непосредственный справочный материал по величине некоторого параметра Р (тело таблицы в виде совокупности значений параметра Р(i,j) чаще всего имеет форму матрицы), и характеристиками таблицы А и В, которые обеспечивают выбор Р(i,j) по значениям А(i) – характеристикам строк и значениям В(j) – характеристикам столбцов таблицы, которые представляют собой векторы. Векторы А и В обычно упорядочены и значения А(i) и В(j) расположены по возрастающей. Параметры тела таблицы Р(i,j) могут размещаться в матрице тела таблицы как упорядочено (по возрастающей или убывающей), так и неупорядочено, то есть хаотично или частично возрастающими и частично убывающими.

Характеристики строк и граф таблицы

Тело таблицы

Рис. 6.13. Общий вид произвольной справочной таблицы

Использование справочных таблиц в общей структуре программы расчета химико-технологического процесса или аппарата возможно по двум вариантам: по прямой и по обратной задаче работы с табличным материалом.

Прямая задача использования табличного материала

заключается в том, что по ходу выполнения программы расчета основной задачи рассчитываются параметры АР и ВР , называемые адресами поиска решения, для которых необходимо найти соответствующее значение параметра тела таблицы Р(i,j). Например, для расчета гидравлического

потока плотностью ; – коэффициент гидравлического сопротивления;

необходимо знать величину коэффициента . В общем случае

аппарата. Зависимость (6.7) оформлена в виде таблицы (рис. 6.13), в

значения , которые соответствуют определенным значениям А(i) и В(j) . В результате расчета основной задачи рассчитываются число Рейнольдса Re РАСЧ и относительная шероховатость РАСЧ , которые выступают как адреса поиска решения задачи АР и ВР.

Алгоритм решения прямой задачи (при условии введения в

программу расчета вектора характеристики строк А(i) , вектора характеристики столбцов В(j) , матрицы параметров тела таблицы Р(i,j) и адресов поиска решения задачи АР и ВР) следующий:

1.Сравнивая значения адреса поиска решения задачи АР и вектора характеристики строк А(i), находят такой номер строки i , при которой обеспечивается приемлемое с позиций решаемой задачи значение А(i), например, значение А(i) ближайшее большее по отношению к АР (возможен и иной вариант поиска номера строки i – значение А(i)i должно быть ближайшим меньшим по отношению к АР .

2.Сравнивая значения адреса поиска решения задачи ВР и вектора характеристики строк В(j) , находят такой номер столбца j , при котором обеспечивается приемлемое с позиций решаемой задачи значение В(j), например, значение В(j) , ближайшее большее по

отношению к BР (возможен и иной вариант поиска номера столбца j – значение В(j) должно быть ближайшим меньшим по отношению к BР ).

3.Зная номера строки i и столбца j мы можем в дальнейших расчетах использовать параметр тела таблицы Р(i,j), имеющий эти индексы.

Целесообразно найденные значения i и j запоминать в

если фрагмент расчета с участием Р(i,j) удален от фрагмента расчета позиции определения Р(i,j), и в программе между этими фрагментами будут находиться циклические операции с использованием i и j , то найденные

184

при решении задачи с табличными материалами значения индексов i и j будут утеряны.

В тех случаях, когда значения параметра тела таблицы Р(i,j) существенно различаются между собой для i -й и (i +1)-й строк и для j-го и (j +1)-го столбцов, то для использования в расчетах более правильного значения параметра Р можно произвести его линейную интерполяцию в границах i -й и (i +1)-й строк и j-го и (j +1)-го столбцов. Для этого сначала следует выполнить линейную интерполяцию значений параметра Р(i,j) сначала для i-й строки по столбцам j и j+1

и, наконец, интерполируя решение между i и i+1 строками находим искомое значение интерполированного параметра Pint erpol :

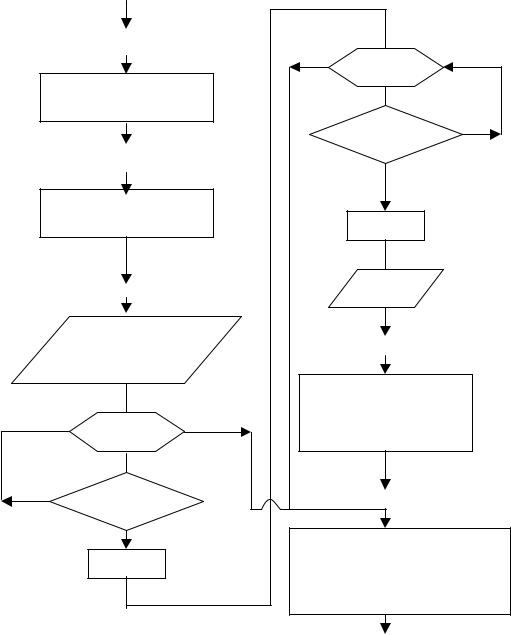
На рис. 6.14 приведена блок-схема решения прямой задачи использования табличного материала без применения интерполяционного поиска параметра тела таблицы.

Обратная задача использования табличного материала

заключается в том, что по ходу выполнения программы расчета основной задачи рассчитывается параметр РР , соответствующий по физической сущности параметру тела таблицы Р(i,j) , и в этом случае необходимо в таблице найти значение Р(i,j) , ближайшее к РР , выявить соответствующие Р(i,j) значения индекса строки i и индекса столбца j и по ним извлечь из таблицы в дальнейший расчет характеристики строки А(i) и столбца В(j) . Например, таблица представляет собой информацию о стандартных теплообменниках одинаковой конструкции, но различных размеров, причем характеристики строк А(i) представляют собой число труб в различных теплообменниках, характеристики столбцов В(j) – это длина труб трубного пучка в различных теплообменниках , а параметры тела таблицы Р(i,j) – поверхность теплообмена для теплообменника с конкретным числом и длиной труб в трубном пучке. Тогда , если в ходе

186

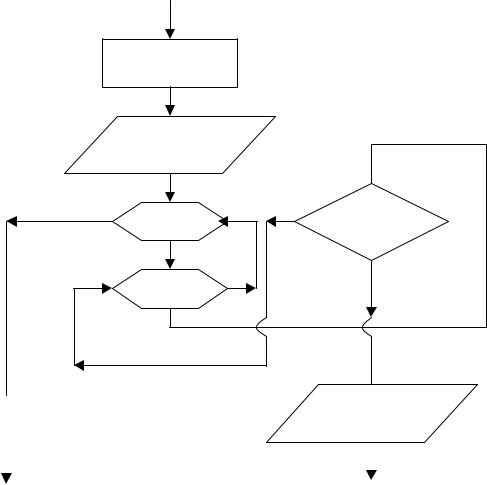
Если используемая таблица содержит упорядоченные значения параметров тела таблицы, то чтобы найти значение Р(i,j) , ближайшее к РР, достаточно сравнивать последовательно Р(i,j) и РР и уже первое сравнение, удовлетворяющее постановке задачи (например, Р(i,j) больше РР ) позволяет выявить соответствующие Р(i,j) значения индекса строки i и индекса столбца j (рис.6.15).

Рис. 6.15. . Блок-схема решения обратной задачи использования табличного материала при условии, что адрес поиска РР должен быть меньше соответствующего параметра тела таблицы Р(i,j) , в случае упорядоченных параметров тела таблицы

Если используемая таблица содержит неупорядоченные значения параметров тела таблицы, то чтобы найти значение Р(i,j) , ближайшее к РР, необходимо сравнивать последовательно все значения Р(i,j) и РР , выявить те значения Р(i,j) , которые удовлетворяют постановке задачи (например, Р(i,j) больше РР ), отобрать их всех приемлемых значений Р(i,j) то, которое ближе всего к величине адреса поиска решения РР, и уже для наилучшего решения задачи Р(i,j) выявить соответствующие ему значения индекса строки i и индекса столбца j (рис.6.16). Для этого в блок-схему решения

188

СПИСОК ЛИТЕРАТУРЫ

1.Кафаров В.В. Методы кибернетики в химии и химической технологии.

– М.: Химия. – 1985. – 447 с.

2.Бояринов А.И.,Кафаров В.В. Методы оптимизации в химической технологии. – М.: Химия. –1971. – 575 с.

3.Касаткин А.Г. Основные процессы и аппараты химической технологии. Изд. 10, стереотипное, доработанное. – М.: Альянс. –2004. – 750 с.

4.Общий курс процессов и аппаратов химической технологии./ Под. ред. Айнштейна В.Г. – М. : Логос, Высшая школа. – Книга 1. – 2002. – 890 с.

5.Общий курс процессов и аппаратов химической технологии./ Под. ред. Айнштейна В.Г. – М. : Логос, Высшая школа. – Книга 2. – 20023 – 8911758 с.

6.Закгейм А.Ю. Введение в моделирование химико-технологических процессов. – М.: Химия. – 1982. – 223 с.

7.Александров И.А. Ректификационные и абсорбционные аппараты. Методы расчета и основы конструирования . – М.: Химия. – 1978. – 280 с.

8.Кельцев Н.В. Основы адсорбционной техники. М.: Химия. – 1984. – 591 с.

9.Тодес О.М., Себалло В.А., Гольцикер А.Д. Массовая кристаллизация из растворов. – Л.: Химия. – 1984. – 232 с.

10.Дытнерский Ю.И. Процессы и аппараты химической технологии. М.: Химия. – 1995. – 768 с.

11.Холланд Ч.Д. Многокомпонентная ректификация. Пер. с англ./Под ред. В.М.Платонова. – М.: Химия. – 1969. – 351 с.

12.Шестопалов В.В. и др. Исследование промышленных ректификационных колонн методом математического моделирования. // Химия и

технология топлив и масел. – 1978. – №2. – С. 9-11.

13.Иванов В.В. Методы вычислений на ЭВМ – Киев: Наукова думка. –

1986. – 582 с.

14 Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Физматгиз. – 1963. – 330 с.

15.Самойлов Н.А. Примеры и задачи по курсу «Применение ЭВМ в химической технологии. Уфа: Изд. УГНТУ. – 2002. – 163 с.

16.Адлер Ю.П., Маркова Н.Б., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: Химия. – 1976. – 279 с.

17.Мухутдинов Р.Х., Самойлов Н.А. Термокаталитическое окисление органических соединений в выбросах . //Химия и технология топлив и масел. – 1982.– №6. – С. 21-23.

189

18.Рузинов Л.П., Слободчикова Р.И. Планирование эксперимента в химии

ихимической технологии. – М.: Химия. – 1976. – 279 с.

19.Мухутдинов Р.Х., Самойлов Н.А. Определение параметров катализаторного слоя в реакторах очистки выбросов в атмосферу от

углеводородов. //Химическое и нефтяное машиностроение. – 1981. –№ 12. – С. 21-23.

190

ПРИЛОЖЕНИЕ

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ДОМАШНИХ И КУРСОВЫХ РАБОТ

Цель работы : закрепление теоретического материала и самостоятельное решение конкретной технологической задачи небольшого объема на ЭВМ, в ходе которого необходимо:

привести краткую теоретическую часть, в которой необходимо рассмотреть общие принципы математического моделирования, связанные с решением поставленной задачи;

уяснить физическую сущность решаемой задачи;составить математическое описание решаемой задачи;

принять численные значения параметров входа решаемой задачи;найти в справочной литературе необходимые недостающие численные

значения параметров; если справочные данные представляют собой табличный или графический материал, то эти данные должны быть введены в программу расчета с запрограммированным извлечением необходимой справочной величины, графический или табличный материал может быть обработан методом наименьших квадратов с получением уравнения регрессии, вводимого далее в программу расчета;

дать характеристику численных методов решения, используемых в расчетах;

составить алгоритм, блок-схему и программу расчета задачи на ЭВМ;привести список идентификаторов программы;выполнить расчет контрольного примера ( ручной счет );в качестве

контрольного примера могут быть рассмотрены полный расчет задачи (при небольшом ее объеме), расчет характерного фрагмента задачи, расчет нескольких итераций при итеративных расчетах и т.п. решения;выполнить отладку разработанной программы, просчитать контрольный

пример на ЭВМ;провести на ЭВМ исследование процесса в границах решаемой задачи,

при этом необходимо выполнить варьирование одного из важнейших параметров входа и рассчитать его влияние на один из важнейших параметров выхода, выполнить анализ полученных вариантов решения задач.

В отчете по выполненной работе (пояснительной записке к курсовой работе) должны быть отражены все вышеперечисленные этапы работы.