
samoilov_n_a_modelirovanie_v_himicheskoi_tehnol
.pdf
111
Корреляционный анализ
Сопоставление ряда моделей, разработанных для описания конкретного процесса, и выбор наилучшей модели удобно выполнять при помощи корреляционного отношения 0 1, рассчитываемого по уравнению
|
|
1 |
( N l )S OCT2 |
. |
(4.18) |
|
( N 1 )SY2 |
||||||
|
|
|
Чем больше величина , темлучше анализируемое уравнение описывает процесс. Если уравнение математической модели учитывает ряд переменных Y f ( X1 , X2 ,..., Xk ) , то используют метод множественной
корреляции, учитывающий коррелируемость между Y и каждым X i . Коэффициент корреляции r* характеризует качество разработанного
уравнения регрессии; так, например, для линейного уравнения регрессии
у = bo + b1х, |
(4.19) |
где bo и b1 – эмпирические коэффициенты; х и у соответственно условия проведения и результат процесса, коэффициент корреляции может быть рассчитан по уравнению
|
N |
N |
2 |
|
|
|
N xi2 |
yi2 |
|
|
|
r b1 |
i 1 |
i 1 |
|
|
|
N |
N |
2 |
|
|
|
|
N yi2 |
yi |
|
(4.20) |
|
|
i 1 |
i 1 |
. |
||
Величина r* - оценивает силу линейной связи и лежит в пределах
0<r*<1. В уравнении (2.19) хi |
и уi – опытные значения; b1 – расчетное |
||
значение коэффициента уравнения регрессии, |
полученное, |
например, |
|
обработкой опытных данных методом наименьших квадратов . |
|
||
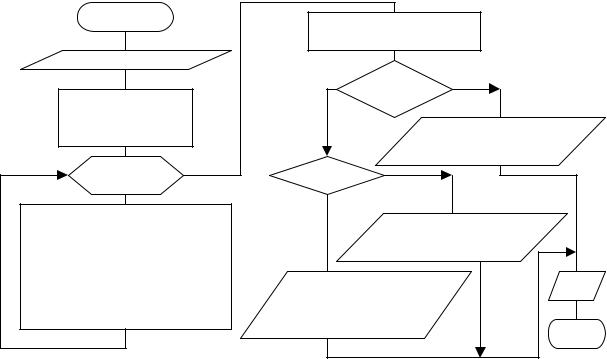
Блок-схема решения задачи приведена на рис. 4.3. |
|
||
В блок-схеме расчета |
коэффициента |
корреляции |
символами |
SX ,SY ,SX 2,SY 2 обозначены соответствующие суммы |
параметров |
||
X ,Y , X 2 ,Y 2 уравнения 4.20. |
|
|
|
112
Начало |
Расчет r * по (4.20) |
|
|
|
|
||
b1 , N, x(N ),Y (N ) |
нет |
да |
|
|
|
||
SX 0, SY 0, |
|
r * 0.9 |
|
|
|
|
|
SX 2 0, SY 0 |
|
Уравнение регрессии |
|
i 1, N |
r * 0.6 |
качественное |
|
|
|
||
SX SX X (i) |
|
да |
|
нет |
Уравнение регрессии |
|
|
SY SY Y (i) |
|
низкого качества |
|
SX 2 SX 2 x(i) x(i) |
Уравнение регрессии |
r * |
|
SY 2 SY 2 y(i) x(i) |
некачественное |
|
|
|
Конец |
||
|
|
|
|
Рис. 4.3. Блок-схема расчета коэффициента корреляции
4.3.Устранение причин неадекватности математической модели
Входе оценки адекватности математической модели исследователь имеет возможность активно вторгаться в процесс формирования модели, повышать или понижать ее параметрическую чувствительность, особенно
втех случаях, когда расчетные статистические критерии приближаются к критическим табличным значениям, незначительно не доходя до условий достижения адекватности.
Вряде случаев, когда неадекватность модели обуславливается низким качеством эксперимента (большой величиной дисперсии воспроизводимости), удается улучшить результаты регрессионного анализа и «исправить» модель за счет постановки дополнительных опытов, выполненных более тщательно, чем основная выборка. Дополнительные опыты могут привести к снижению дисперсии воспроизводимости, повышению уровня параметрической чувствительности модели, коррекции параметров модели (коэффициентов уравнения регрессии) и переводу ее из неадекватной в адекватную форму.
Вкачестве примера рассмотрим зависимость глубины гидроочистки дизельного топлива от температуры, давления и других факторов
113
процесса. При разработке стохастической модели в форме уравнения регрессии установлено, что значимость одного из коэффициентов уравнения, учитывающего влияние температуры на процесс гидроочистки, определяется величиной критерия Стьюдента, равной двум. При жестком подходе к решению задачи (вероятность ошибочного суждения о значимости коэффициента Р=0.02), расчетный критерий Стьюдента меньше табличного, равного 2.896. Таким образом, необходимо сделать вывод, что температура является незначимым фактором процесса гидроочистки или что отсутствует параметрическая чувствительность процесса к температуре в выполненных экспериментах. Однако, такая чисто формальная оценка ситуации может существенно исказить представления о процессе в ходе его дальнейшего компьютерного моделирования. Поэтому необходимо установить причины параметрической нечувствительности модели к температуре. Возможны две альтернативные ситуации:
параметры модели изменялись в ходе экспериментов в узком диапазоне изменения температур процесса гидроочистки, то есть по сути дела разрабатывалась изотермическая модель процесса и параметрическая нечувствительность естественна;
существенная погрешность измерений привела к неверным исходным значениям температуры при разработке модели и завышению дисперсии воспроизводимости.
После установления причин неадекватности модели можно улучшить ее, например, расширением диапазона исследуемых температур, проведением дополнительных опытов, использования менее жесткого подхода к оценке значимости модели (например, при Р=0.1 табличный критерий Стьюдента становится равным 1.860, что меньше его расчетной величины, равной двум), что переводит температуру в разряд значимых факторов.
При детальной оценке адекватности модели используют различные подходы к самому понятию адекватности.
Так, например, если критерий Фишера меньше или равен табличному, то говорят об адекватности состояния модели (адекватности описания опытных данных); если остаточная дисперсия приближается к величине дисперсии воспроизводимости и критерий Фишера близок к единице , то говорят об адекватности уравнения. В том случае, когда модель качественно описывает поведение процесса, но количественные результаты моделирования оставляют желать лучшего (чрезмерно большие расхождения между опытными и расчетными данными), говорят об адекватности поведения модели.
114
ГЛАВА 5. МЕТОДЫ ОПТИМИЗАЦИИ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Под оптимизацией математических моделей понимают поиск таких значений параметров химико-технологической системы, при которых она функционирует наилучшим способом. Для оптимизации химикотехнологической системы необходимо разработать критерий
оптимальности R – параметр выхода системы, значение которого лежит в основе оценки показателей процесса при выборе его оптимальных
показателей, при этом величина критерия R должна принимать экстремальное (минимальное или максимальное) значение. Критерий оптимальности связан с параметрами оптимизируемого процесса целевой функцией
R R(X1 , X 2 ,..., X N ) , |
(5.1) |
где X i – оптимизируемые параметры (температура, |
давление, расход |
реагентов и т.д.). |
|
Различают два класса критериев оптимальности: |
|
технологические критерии оптимальности: максимальный выход или качество продуктов, минимальный объем технологических аппаратов, минимальное содержание примесей в целевом продукте и т.д.;
экономические критерии оптимальности: минимальные себестоимость, капитальные и эксплуатационные затраты, энергозатраты, максимальная прибыль от реализации продукции и т.д.
При решении задачи оптимизации можно использовать только один критерий, поэтому сложность выбора критерия оптимальности заключается в том, чтобы из возможного набора критериев найти такой, чтобы он при существующих требованиях к производству являлся основополагающим. Например, при разработке нового процесса критерием его оптимальности может быть достижение максимального выхода целевого продукта, а при выборе варианта технологической схемы производства продукта, который может быть получен разными способами, в качестве критерия оптимальности может выступать себестоимость(при условии, что различные способы производства обеспечивают одинаковый выход целевого продукта. При попытке использовать два или более критериев оптимальности для решения одной задачи получают по каждому из них свои индивидуальные, не согласующиеся друг с другом , условия оптимизации.
Целевая функция может представлять собой как непосредственно математическую модель процесса, так и формироваться специально для
|
115 |
|
|
целей оптимизации, например, можно составить частную экономическую |
|||
модель процесса и дополнить ею ранее разработанную полную модель. |
|||
Особенностью сложных целевых функций является возможность |
|||
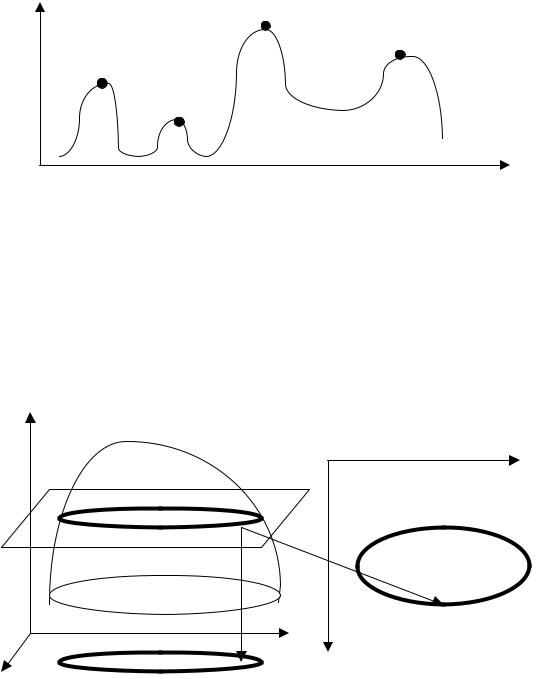
наличия в них нескольких вариантов оптимальных решений (например, |
|||
несколько максимумов (рис. 5.1), в этом случае задачей оптимизации |
|||
является поиск глобального экстремума – наибольшего из максимумов или |
|||
наименьшего из минимумов. |
|
|
|
|
RMAX ,3 = RG |
|
|
R |
RMAX ,1 |
RMAX ,4 |
|
|
|
|
|
|
RMAX ,2 |
|
|
|
|
X |
|
Рис. 5.1. Полиэкстремальная зависимость R R(X )=МАХ |
|||
|
RG – глобальный экстремум |
|
|
При оптимизации двухпараметрических задач целевая функция |
|||
представляет собой поверхность (рис.5.2) и для наглядности расчетов ее |
|||
часто рассекают поверхностями равного уровня при значениях критерия |
|||
R const , |
проектируя на плоскость |
X1 , X 2 линии равного уровня, |
|
получаемые при пересечении поверхности R R(X1 , X 2 ) |
плоскостью |
||
R const . |
|
|
|
R |
R R( X 1 , X 2 ) |
X 1 |
|
|
R const |
|
|
|
X 1 |
X 2 |
|
X 2 |
а |
|
б |
Рис. 5.2. Представление линий равного уровня (жирные линии) |
|||
|
в трехмерном (а) и двухмерном пространстве (б) |
|
|
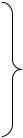
116
Поиск координат экстремума целевой функции может выполняться различными методами оптимизации, выбор конкретного метода обуславливается спецификой целевой функции, наличием ограничений на решение задачи, быстродействием метода и рядом других факторов. Методы решения задач оптимизации можно классифицировать по нескольким видам, относительно просты по решению и математическому аппарату:
метод классического аналитического поиска экстремума;метод неопределенных множителей Лагранжа;группа методов нелинейного программирования;группа методов линейного программирования;группа методов динамического программирования,методы стохастической оптимизации на.
5.1. Метод классического аналитического поиска экстремума
Метод основан на том, что целевая функция
R R( X1 , X 2 ,..., X i ,..., X N )=МАХ |
(5.2) |
действительно имеет экстремум, если в точке, подозреваемой на наличие экстремума, производные R / X i 0 (необходимое условие экстремума)
и в окрестности точки, |
подозреваемой на наличие экстремума, меняется |
|||||
знак производной R / X i |
(достаточное |
условие). Таким образом, |
||||
решение задачи сводится к формированию системы уравнений |
|
|||||
|
|
R / X1 |
0 |
|
|
|
|
|
R / X 2 |
0 |
|
|
|
|
|
|
… |
|
|
|
|
|
R / X i |
0 |
, |
(5.3) |
|
|
|
|
… |
|
|
|
|
|
R / X N |
0 |
|
|
|
решение |
которой |
дает |
оптимальные |
значения |
параметров |
|
X1,ОПТ ,..., X N ,ОПТ .
Классический аналитический метод поиска экстремума обычно применяют, когда формирование уравнений R / X i 0 не представляет
труда и решение системы уравнений (5.3) достаточно несложно.
В качестве примера применения метода рассмотрим задачу об определении оптимальных условий реализации химической реакции.

117
Пусть обратимая изотермическая реакция первого порядка
А 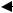 В протекает в газовой фазе в аппарате с псевдоожиженным слоем
В протекает в газовой фазе в аппарате с псевдоожиженным слоем
катализатора. |
В |
ходе процесса |
происходит постепенное истирание |
катализатора |
и |
его унос в виде |
пыли с продуктами реакции. Найти |
оптимальные значения температуры процесса Топт и продолжительности пребывания реакционной смеси в зоне реакции опт, при которых минимизируются стоимость потерь катализатора и непрореагировавшего сырья [2].
В данной задаче в качестве критерия оптимальности R можно рассматривать сумму потерь катализатора и непрореагировавшего сырья; целевая функция может быть записана в этом случае в общем виде как
R = SA CAк + SvV = (SA CAк + Sv p ) = min , |
(5.4) |
где - расход сырья, м3/с;
SA – стоимость единицы объема исходного сырья, р/м3;
CAк – конечная концентрация компонента А в реакционной смеси, м3/м3;
Sv – стоимость потерь катализатора с единицы объема рабочей зоны реактора, р/м3 с;
V - объем рабочей зоны реактора (объем псевдоожиженного слоя), м3;p – продолжительность реакции, с.
При заданных , SA и Sv для решения (5.4) необходимо знать
величины CAк и (или V), взаимосвязь которых |
формируется в |
||
математической модели процесса. |
|
||
Математическая модель кинетики реакции по сырьевому |
|||
компоненту А имеет вид |
|
||
|
dC A |
K1C Ak K 2 CBk |
|
|
|
|
|
|
d |
|
|
, |
(5.5) |
||
Кi = koi exp[ Ei /(R T)] |
|
||
где К1 и К2 – константы скорости прямой и обратной реакций, с-1;
koi – предэкспоненциальный множитель, с-1; Еi – энергия активации , Дж/моль;
Т – абсолютная температура проведения реакции, К; R – универсальная газовая постоянная;

118
CBk – конечная концентрация компонента В в реакционной смеси, м3/м3.
Модель гидродинамики реактора с псевдоожиженным слоем катализатора соответствует требованиям идеального смешения и по компоненту А может быть записана как
dC A 1 C A0 C Ak , |
(5.6) |
|
d |
P |
|
где СA0 - начальная концентрация А в исходном сырье, м3/м3.
Полная математическая модель реактора по компоненту А имеет вид
dC A |
|
1 |
|
|
|
|
|
|
|
|
|
(СA0 |
C Ak ) ko 1{exp[ E1 |
/(R |
T )]}C Ak |
|
|
d |
|
|
||||||
|
P |
|
|
|
|
|
||
ko2 {exp[ E2 |
/(R T)]}C Вk |
|
|
. |
(5.7) |
|||
Полная модель реактора по компоненту В может быть записана в форме дифференциального уравнения аналогично (5.7), но проще ее в данной задаче использовать в форме алгебраического уравнения
СВk СА0 САk СВ0 , (5.8)
где СВ0 – начальная концентрация компонентов В в исходном сырье (при
отсутствии рециркуляции |
непрореагировавшего сырья СВ0 обычно |
равна нулю). |
|
Решая совместно (5.7) и (5.8) для стационарных условий реализации |
|
процесса (dCA /d =0) при СВ0 |
= 0 при = 0, получаем следующее уравнение |
математического описания реактора с псевдоожиженным слоем катализатора:
СAк C Ao |
1 P ko 1 exp[ E1 /(R T)] |
|
, |
|
1 P {ko1 exp[E1 /(R T )] ko2 exp[ E2 /(R T )]} |
(5.9) |
|||
подстановка которого в (5.7) позволяет сформировать целевую функцию в окончательном виде:
|
1 P ko1 exp[ E1 /(R T )] |
|
|
|
|
||
R S AC A0 |
|
|
|
|
|
|
SV P |
|
T )] ko2 |
exp[ E2 |
|
T )]) |
|||
|
1 P (ko1 exp[ E1 /(R |
/(R |
|
||||
|
= MIN . |
|
|
|
|
(5.10) |
|
119
В результате дифференцирования (5.10) по Р и Т получим систему уравнений, определяющих позицию экстремума целевой функции
dR |
|
|
|
|
|
|
|
E1 / R T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ko e |
|
|
|
|
|
|
|
||
|
|
S |
S |
|
|
|
1 |
|
|
|
S |
|
0 |
|||
|
|
A |
1 P (ko e E1 / R T ko e E2 / R N ) 2 |
|
||||||||||||
d P |
|
|
A |
|
v |
|
||||||||||
|
|
|
|
o |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
, (5.11) |
|
|
SACA Pko e E1 / R T P (E2 E1) ko e E2 / R T E1 |
||||||||||||||
dR |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dT |
|
|
|
|
R T2 1 P |
(ko e E1 / R T ko |
e E2 / R T ) 2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
решение которой позволяет рассчитать Т=Топт и = опт .
Нелинейную систему (5.11) можно решить на ЭВМ двумя способами:
– решением собственно нелинейной системы (5.11), например, методом простых или модифицированных итераций, приведя её к виду
|
|
|
|
|
|
k e E1 / R T |
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
S S |
|
|
1 |
S |
|
|
|
|
p |
|
(ko e E1 / R T ko e E2 / R N ) 2 |
|
P |
||||||
|
|
A A |
v |
|
||||||
|
|
|
o 1 P |
|
|
|
|
|||
|
|
|
|
|
1 |
2 |
|
|
|
|
T SAC Ao P ko2 e E1 / R T P (E2 E1 )ko2 e E2 / R T E1 T |
, |
(5.12) |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
– преобразованием системы уравнений (5.11) в форму |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
( |
S A |
Co ko |
|
e |
E / R T |
) |
0,5 |
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Sv |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ko |
|
|
T ko |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
e E2 / R |
e E2 / R |
T |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
, |
(5.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
P |
(E |
2 |
E )k |
o2 |
e E2 / R T E 0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
||||
с получением уравнения с одной переменной Т |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E2 / R*T |
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
E1 |
|
|
|
|
ko2e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(T) |
|
|
|
|
|
|
|
|
|
|
SA |
C k e |
E1 / R*T |
1 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
k e E2 |
|
|
|
|
||||||||||||
|
E E k e E1/ R*T |
/ R*T S |
|
Ao o1 |
|
|
||||||||||||||||||
2 1 |
01 |
|
|
|
|
|
|
|
02 |
|
|
|
|
|
|
V |
|
|
|
|
, (5.14) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

120
позволяющим любым алгоритмом поиска корня (методами сканирования, хорд, касательных, половинного деления и др.) рассчитать на ЭВМ оптимальную температуру Т=ТОПТ, которая затем используется для расчетаОПТ по любому уравнению системы (5.14).
5.2. Метод неопределенных множителей Лагранжа
Метод применяется в тех случаях, когда на оптимизируемый процесс накладывается несколько (k ) ограничений в виде
fi ( X1 , X 2 ,..., X i ,..., X M ) 0 |
i 1,2,..., M , |
(5.15) |
где число параметров, входящих в функции ограничений M N – числа параметров, входящих в функцию оптимизации (5.2). В методе Лагранжа формируется Функция Лагранжа
|
k |
|
|
L R( X1 , X2 ,..., X N ) i fi ( X1 , X2 ,..., X M |
) MAX ( MIN ) , |
(5.16) |
|
|
i 1 |
|
|
где i – |
неопределенные множители Лагранжа (неизвестные |
числа); |
|
R( X1 , X 2 ,..., X N )–целевая функция. |
|
|
|
Не |
вдаваясь в теоретические основы |
метода, отметим, что если |
|
целевая функция при некоторых оптимальных значениях параметров Х стремится к экстремумы, то очевидно, что добавление к целевой функции нулевых по (5.15) функций ограничения не изменит значения критерия оптимальности и равной ему функции Лагранжа в экстремальной точке. Координаты экстремума X1,ОПТ ,..., X N ,ОПТ находят из условия равенства нулю первых производных функции Лагранжа по параметрам процесса
X j и неопределенным множителям i :
L / X1 0 |
|
|
|
… |
|
|
|
L / X j |
0 |
|
|
… |
|
|
|
L / X N |
0 |
, |
(5.17) |
L / 1 0 |
|
|
|
… |
|
|
|
L / i |
0 |
|
|
… |
|
|
|
L / k 0
