
samoilov_n_a_modelirovanie_v_himicheskoi_tehnol
.pdf
|
|
101 |
|
|
|
Композиционная |
матрица |
с |
псевдолинейными |
столбцами |
|
|
|
|
N |
|
|
приобретает свойство |
ортогональности |
( ( xi , j xu , j |
) 0 )и |
позволяет |
|
|
|
|
i 1 |
|
|
разработать с учетом формулы для расчета коэффициентов уравнения регрессии
N
|
|
bj |
|
Yi x j ,i |
|
|
|
|
|
|
|
i 1 |
|
|
|
(3.61) |
|
|
|
|
N |
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
x 2j ,i |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
разработать псевдолинейное уравнение регрессии |
|
|
||||||
? |
b0 x0 b1 x1 |
b2 x2 |
b12 x1 x 2 |
b1 x1 |
b2 x 2 . (3.62) |
|||
Y |
||||||||
После расчета |
коэффициентов псевдолинейного |
уравнения |
||||||
регрессии (3.62) его переводят в квадратичную форму уравнения регрессии
(3.58) , заменяя псевдолинейные члены x j второй формулой кодирования
(3.60), при этом, после приведения подобных членов уравнения, изменится только величина свободного члена уравнения b0 :
|
N |
|
|
|
M |
x2j ,i |
|
|
|
b0( 3.56 ) b0( 3.60 ) ( bj |
i 1 |
) , |
(3.63) |
|
N |
||||
j 1 |
|
|
где М – число псевдолинейных членов уравнения (3.62).
При необходимости полученное квадратичное уравнение регрессии переводят из кодированной формы в натуральную, заменяя кодированные параметры первой формулой кодирования (3.31).
Недостатком композиционных ортогональных планов второго порядка является то, что при расчете различных видов коэффициентов уравнения регрессии учитывается различное число опытов, например в уравнении (3.58) коэффициенты b0 , b11 , b22 рассчитываются по результатам 9 опытов (табл.3.10), b1 , b2 – 6 опытов, b12 – 4 опытов. Этот недостаток устраняется в ротатабельных композиционных планах второго порядка, однако они не ортогональны и его коэффициенты рассчитывают методом наименьших квадратов в полном объеме.
102
ГЛАВА 4. МЕТОДЫ ОЦЕНКИ АДЕКВАТНОСТИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Адекватность модели реальному объекту оценивается по близости результатов расчетов по модели контрольным экспериментальным данным. Методы оценки адекватности можно разделить на субъективные и объективные, в последнем случае оценка адекватности выполняется независимо от мнения исследователя по специальным критериям.
4.1. Субъективные методы оценки адекватности
Оценка близости значений экспериментальных и расчетных данных
Наиболее |
часто |
используются |
при |
сопоставлении |
||||
экспериментальных |
и расчетных данных |
|
понятия |
абсолютной Y и |
||||
относительной Y погрешности расчета: |
|
|
|
|
||||
|
|
Y YE YM , |
|
(4.1) |
||||
|
Y |
|
YE YM |
|
/ YE , |
|
(4.2) |
|
|
|
|
|
|||||
где YE ,YM – экспериментальный и расчетный по модели результат процесса в сходственных точках, то есть при одинаковых значениях
параметров процесса Xi . Традиционно результаты расчета по модели считались удовлетворительными при величине относительной погрешности 5%, что определялось погрешностью расчетов при помощи логарифмической линейки. Естественно, что при компьютерных расчетах допустимая величина Y существенно уменьшается. При недостаточной проработке математического описания или весьма существенных допущениях, принятых при разработке математической модели, погрешность Y может достигать 10-20%. Так, например, при расчете потерь напора в трубчатой печи в зоне испарения продукта в камере радиации по методу Бакланова принято допущение о постоянстве теплонапряженности поверхности трубчатого змеевика, что приводит к погрешности расчета потерь напора до 20%. В пионерских, приближенных математических моделях не имеющих аналогов достижение расчетных
103
значений одного порядка с опытными уже является вполне приличным результатом.
Выражение экспериментальных данных в линейных анаморфозах математической модели
Чтобы установить формальную приемлемость нелинейной предлагаемой математической модели Y f ( X ) для описания реального объекта, уравнение Y f ( X ) преобразуют (если есть такая возможность) влинейный эквивлент (анаморфозу) Z (U ), причем в общем случае Z (Y ), а U F( X ) . Если опытные точки достаточно корректно укладываются в линейную анаморфозу, то это является
формальным |
свидетельством |
возможности |
использования |
моделиY f ( X ) |
для описания |
процесса и, кроме |
того, линейная |
анаморфоза упрощает расчет параметров модели по методу наименьших квадратов.
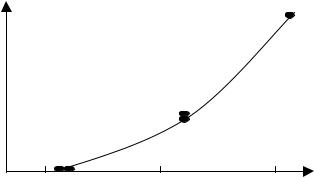
В качестве примера рассмотрим подбор формы уравнения регрессии по линейной анаморфозе опытных данных по термокаталитической очистке отходящих газов от паров метилметакрилата на оксидном железохромовом катализаторе позволили рассчитать значение константы скорости реакции окисления метилметакрилата k для ряда температур t (0С) (табл. 4.1) [17]; зависимость k = f ( t ) (рис. 4.1) имеет вид достаточно характерный, похожий на экспоненциальную зависимость. Требуется
определить, можно ли описать k = f ( t ) |
уравнением Аррениуса |
k= kо e –E/RT , |
(4.3) |
где kо – предэкспоненциальный множитель; Е – энергия активации; R– универсальная газовая постоянная; Т – абсолютная температура.
k, с-1
60 –
50 –
40 –
30 –
20 –
10 –
0
200 |
300 |
400 t ,0С |
Рис. 4.1. Зависимость константы скорости реакции k от температуры окисления метилметакрилата t
104
Таблица 4.1 Опытные данные по окислению паров метилметакрилата
Температура, оС |
Степень очистки, % |
k, с-1 |
ln k |
210 |
10,95 |
1,437 |
0,362 |
210 |
11,42 |
1,502 |
0,406 |
220 |
35,30 |
1,830 |
0,604 |
220 |
33,40 |
1,730 |
0,548 |
330 |
76,83 |
22,601 |
3,113 |
330 |
72,22 |
19,796 |
2,985 |
420 |
97,56 |
65,953 |
4,189 |
Чтобы оценить возможность описания данной экспериментальной зависимости уравнением Аррениуса, рассмотрим линейную анаморфозу (линейную форму) уравнения Аррениуса; для этого прологарифмируем уравнение (4.3):
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
lnk= lnko – (E/R) |
|
|
|
|
|
|
|
||||
|
Т |
. |
|
(4.4) |
|||||||||
Очевидно, что если опытные |
lnk |
|
|
|
|
|
|
|
|
||||
данные в координатах (lnk) – (1/Т) |
|
|
|
|
|
|
|
|
|
||||
будут удовлетворительно уклады- |
|
|
|
|
|
|
|
|
|
||||
ваться на линейную зависимость, |
4 |
– |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
||
то функция lnk = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Т может |
|
|
|
|
|
|
|
|
|
||||
быть в принципе описана уравне- |
3 |
– |
|
|
|
|
|||||||
нием (4.4) и соответственно k=f(t) |
|
|
|
|
|
|
|
|
|
||||
будет подчиняться уравнению Ар- |
|
|
|
|
|
|
|
|
|
||||
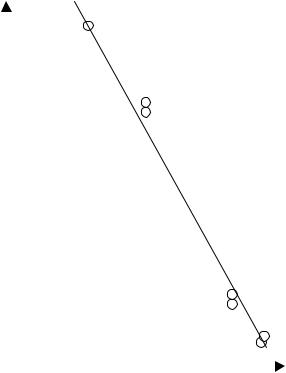
рениуса (4.3). Как |
видно из рис. |
|
|
|
|
|
|
|
|
|
|||
4.2, окисление паров метилметак- |
2 |
– |
|
|
|
|
|||||||
рилата может быть описано урав- |
|
|
|
|
|
|
|
|
|
||||
нением Аррениуса с позиций ка- |
|
|
|
|
|
|
|
|
|
||||
чественного описания адекватно- |
|
|
|
|
|
|
|
|
|
||||
сти поведения и адекватности со- |
1 |
– |
|
|
|
|
|||||||
стояния модели и процесса. Зна- |
|
|
|
|
|
|
|
|
|
||||
чения lnkо = 11,17 и Е = 44,6 кДж/ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
моль, найденные методом наимень- |
|
1.6 |
1.8 |
2.0 |
|||||||||
ших квадратов, позволяют исполь- |
|
|
|
|
|
|
(1/Т)103, К |
||||||
зовать далее уравнение |
Аррениуса |
|
|
|
|
|
|
||||||
при моделировании процесса термо- |
|
|
|
|
|
|
|
ln k (1/ T ) |
|||||
каталитической очистки |
отходя- |
Рис. 4.2. Зависимость |
|||||||||||
щих газов на ЭВМ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
105
4.2. Объективные методы оценки адекватности
Регрессионный анализ
Этот метод оценки адекватности основан на использовании независимых статистических критериев, позволяющих охарактеризовать справедливость исследуемых гипотез. Регрессионный анализ обычно выполняется в три этапа, которые сводятся к оценке воспроизводимости эксперимента, проверке значимости коэффициентов разработанной модели (например, уравнения регрессии) и оценке адекватности модели.
Допустим, что в нашем распоряжении имеется серия экспериментальных данных (выборка) объемом N независимых опытов, в котором каждый случай измерения результата процесса Y повторен в серии параллельных опытов М раз. Для статистической обработки эксперимент должен удовлетворять следующим требованиям:
1)независимые параметры должны измеряться с пренебрежимо малой ошибкой по сравнению с зависимым параметром Xi , так как в ошибку определения Y входят и неучтенные возмущения параметров Xi , например, погрешность измерения температуры, погрешность взвешивания и т.д.;
2)при закрепленных значениях Xi случайная величина Y подчиняется закону нормального распределения;
3)для ряда серий параллельных опытов должно выполняться условие однородности дисперсий (среднеквадратичных отклонений опытных данных относительно среднего значения параметров для серии параллельных опытов).
Для проверки однородности дисперсий, то есть приемлемого качества эксперимента, используется статистический критерий Кохрена. Анализ эксперимента на однородность дисперсий выполняется следующим образом. Для каждой серии из М параллельных опытов рассчитывается выборочная дисперсия S2
|
|
M |
|
|
|
|
|
|
|
|
S2j |
|
(Yi , j |
Yj |
)2 |
|
, j 1,2,..., N , |
|
|||
i 1 |
|
|
|
|
|
(4.5) |
||||
|
|
f |
||||||||
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|||
|
|
|
|
|
Yi , j |
|
|
|||
|
|
|
Y j |
|
i 1 |
|
, |
(4.6) |
||
|
|
|
M |
|||||||
|
|
|
|
|
|
|
||||

106
где N –число независимых опытов, f – число степеней свободы дисперсии, равное числу опытов, по которому рассчитывается данная дисперсия (в нашем случае число параллельных опытов М), за вычетом числа связей, наложенных на расчет дисперсии. Одной связью является один любой параметр, рассчитанный по данной серии из М опытов
(например, расчет Y j – это одна связь) и учтенный при расчете данной
дисперсии. Таким образом, f =М-1.
После расчета выборочных дисперсий для всех серий параллельных
опытов выделяют из них наибольшую дисперсию |
S 2 MAX и рассчитывают |
||
критерий Кохрена G , проверяющий гипотезу «рассматриваемые |
|||
дисперсии однородны»: |
|
||
G |
S2 |
|
|
MAX |
. |
(4.7) |
|
N |
|||
SJ2
j 1
Чем меньше величина критерия Кохрена Б тем выше качество (воспроизводимость) эксперимента, его однородность; дисперсии однородны если
G GP( N ,M 1 ) , |
(4.8) |
где GP( N ,M 1 ) – табличное значение критерия |
Кохрена при уровне |
значимости вероятности ошибки при оценке гипотезы Р и степенях свободы N и М-1.
Дисперсия воспроизводимости S 2 ВОСПР , которая является эквивалентом среднеквадратичной погрешности эксперимента в целом, рассчитывается по формуле
N
S 2j
|
S 2 |
ВОСПР |
j 1 |
|
. |
|
|
|
|
(4.9) |
||||
|
N |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В тех случаях, когда число параллельных |
опытов M j |
в разных |
||||||||||||
сериях неодинаково, дисперсия воспроизводимости рассчитывается как |
||||||||||||||
S 2 |
|
|
S 2 |
f |
1 |
S 2 f |
2 |
... S |
2 |
f |
N |
|
|
|
ВОСПР |
|
1 |
|
2 |
|
N |
|
, |
(4.10) |
|||||
|
|
|
|
f1 f2 |
... f N |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
где f j M j 1, и в этом случае для оценки однородности дисперсий применяется статистический критерий Бартлетта [18].
107
Ранее было показано, что коэффициенты уравнений регрессии могут изменять свою величину в зависимости от объема выборки, то есть, выражаясь языком математической статистики, существует доверительный интервал значений, внутри которого может изменяться величина
коэффициента Bj математической модели процесса. Смысл проверки
значимости коэффициента Bj заключается в проверке гипотезы о наличии
нуля внутри доверительного интервала. Очевидно, если коэффициент Bj
может принять нулевое значение (пусть не в выполненном, а
гипотетическом эксперименте), то слагаемое B j x j можно объявить
незначимым (не влияющим на ход изучаемого процесса)и исключить его из уравнения регрессии.
Оценка значимости коэффициентов выполняется по статистическому
критерию Стьюдента t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t j |
|
Bj |
/ Sb, j |
|
, |
|
|
(4.11) |
||||
|
|
|
|
|
|||||||||
где Sb, j – погрешность |
определения |
коэффициента |
Bj , связанная с |
||||||||||
погрешностью эксперимента. |
|
|
|
|
|
|
|
|
|||||
В общем случае Sb, j |
находят по закону накопления ошибок |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
N B |
j |
2 |
|
|
|
|
|||||
Sb, j |
|
|
|
|
|
|
Si2 |
|
|
||||
|
Y |
|
|
(4.12) |
|||||||||
|
|
i 1 |
i |
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
||||
для ортогональных матриц планирования
|
Sb, j |
|
S2 |
|
|
|
|
ВОСПР |
|
(4.13) |
|||
|
|
|||||
|
|
|
N |
. |
||
Чем больше |
величина |
t j , |
тем |
выше |
вероятность значимости |
|
коэффициента Bj ; |
коэффициент |
Bj значим, |
если расчетная величина |
|||
критерия Стьюдента t j больше табличного значения tP , f (табл. 4.2), где
Р уровень значимости вероятности ошибки при оценке гипотезы о значимости коэффициента, f – число степеней свободы дисперсии
воспроизводимости ( f = N )
108
|
Табличные значения критерия Стьюдента |
Таблица 4.2 |
||||
|
|
|||||
|
|
|
|
|
|
|
Число |
|
Р = 0,2 |
Р = 0,1 |
Р = 0,05 |
Р = 0,02 |
Р = 0,01 |
степеней |
|
|||||
свободы |
|
|
|
|
|
|
|
Р = 0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1,963 |
3,078 |
6,314 |
12,706 |
31,821 |
63,657 |
2 |
1,386 |
1,886 |
3,920 |
4,303 |
6,965 |
9,925 |
3 |
1,250 |
1,638 |
2,353 |
3,182 |
4,541 |
5,841 |
4 |
1,190 |
1,533 |
2,132 |
2,776 |
3,747 |
4,604 |
5 |
1,156 |
1,476 |
2,015 |
2,571 |
3,365 |
4,604 |
6 |
1,134 |
1,440 |
1,943 |
2,447 |
3,143 |
4,032 |
7 |
1,119 |
1,415 |
1,895 |
2,365 |
2,998 |
3,707 |
8 |
1,108 |
1,397 |
1,860 |
2,306 |
2,896 |
3,499 |
9 |
1,100 |
1,383 |
1,833 |
2,262 |
2,821 |
3,355 |
10 |
1,093 |
1,372 |
1,812 |
2,228 |
2,764 |
3,250 |
20 |
1,064 |
1,325 |
1,725 |
2,086 |
2,528 |
2,865 |
30 |
1,055 |
1,310 |
1,697 |
2,042 |
2,457 |
2,750 |
Как следует из табл. 4.2, при оценке значимости коэффициентов допускается довольно широкий диапазон значений вероятности ошибочности гипотезы о значимости – Р изменяется от 0.01 ( суждение о значимости рассматриваемого коэффициента может оказаться ошибочным в одной серии опытов из ста) до 0.3 (суждение о значимости рассматриваемого коэффициента может оказаться ошибочным в тридцати сериях опытов из ста) ; эта гибкость оценок необходима для того, чтобы «оставить в живых» коэффициент уравнения регрессии с небольшим значением критерия Стьюдента (например, 6 при одной степени свободы) , который при жестком подходе к оценке значимости станет незначимым, но по физической сущности процесса очень важен для модели. Например, рассматриваемый коэффициент характеризует температуру химического процесса, которая, как известно, существенно влияет на кинетику
процесса; тогда взяв Р=0.2 получим, что коэффициент значим (t больше
табличного значения tP ) и в дальнейшем модель будет учитывать влияние температуры на ход процесса.
Следует напомнить, что если оказывается незначимым коэффициент уравнения регрессии, полученного в пассивном эксперименте, то, после исключения незначимых слагаемых из уравнения регрессии, все остальные коэффициенты подлежат пересчету по методу наименьших
109
квадратов. Если оказывается незначимым коэффициент уравнения регрессии, полученного в активном эксперименте, то, после исключения
незначимых слагаемых из уравнения регрессии, |
остальные коэффициенты |
||||
не пересчитывают. |
|
|
|
|
|
Гипотеза об адекватности разработанной математической модели |
|||||
проверяется по статистическому критерию Фишера F , в общем случае |
|||||
|
|
F S АД2 / S ВОСПР2 |
, |
(4.14) |
|
где S АД2 , S ВОСПР2 |
– |
соответственно дисперсии |
адекватности и |
||
воспроизводимости. |
S АД2 |
характеризует погрешность разрабатываемой |
|||
математической модели |
относительно |
контрольных опытов, |
|||
S ВОСПР2 характеризует качество контрольных экспериментов. Очевидно, чем менше погрешность модели, тем выше уровень ее адекватности. Математическая модель адекватна , если расчетная величина критерия
Фишера меньше табличного значения FP , f1 , f2 (табл. 4.3), где где Р уровень значимости вероятности ошибки при оценке гипотезы об
адекватности модели, f1 и |
f2 – число степеней свободы дисперсий в |
|||||||
числителе и знаменателе критерия Фишера. |
|
|
Таблица 4.3 |
|||||
|
Таблица значений критерия Фишера |
|
||||||
|
|
|
|
|||||
Число степеней |
Число степеней свободы (f1) для большей дисперсии |
|||||||
свободы (f2) |
||||||||
для меньшей |
|
|
|
|
|
|
|
|
дисперсии |
1 |
|
2 |
3 |
6 |
10 |
|
16 |
|
|
|
||||||
1 |
161 |
|
200 |
216 |
234 |
242 |
|
246 |
2 |
18,5 |
|
19,0 |
19,1 |
19,3 |
19,3 |
|
19,4 |
3 |
10,1 |
|
9,55 |
9,28 |
8,94 |
8,78 |
|
8,69 |
4 |
7,71 |
|
6,94 |
6,59 |
6,16 |
5,96 |
|
5,84 |
5 |
6,61 |
|
5,79 |
5,41 |
4,95 |
4,74 |
|
4,60 |
6 |
5,99 |
|
5,14 |
4,76 |
4,28 |
4,06 |
|
3,92 |
7 |
5,59 |
|
4,74 |
4,35 |
3,87 |
3,63 |
|
3,49 |
8 |
5,32 |
|
4,46 |
4,07 |
3,58 |
3,34 |
|
3,20 |
9 |
5,12 |
|
4,26 |
3,86 |
3,37 |
3,13 |
|
2,98 |
10 |
4,96 |
|
4,10 |
3,71 |
3,22 |
2,97 |
|
2,82 |
12 |
4,75 |
|
3,88 |
3,49 |
3,00 |
2,76 |
|
2,60 |
14 |
4,60 |
|
3,74 |
3,34 |
2,85 |
2,60 |
|
2,44 |
16 |
4,49 |
|
3,63 |
3,24 |
2,74 |
2,49 |
|
2,33 |
18 |
4,41 |
|
3,55 |
3,16 |
2,66 |
2,41 |
|
2,25 |

110
При больших значениях чисел степеней свободы, выходящих за пределы характеристик строк и граф табл. 4.3, величина критерия Фишера близка к двум.
Если эксперимент состоит из N основных опытов, которые выполнены с одинаковым числом опытов в параллельных сериях экспериментов (M1 M2 ... MN ), то
|
N |
|
|
? |
|
2 |
|
|
N M |
|
|
|
2 |
|
|
|
|
) |
Y j ) |
|
|
||||||||||||
|
M |
( Y j Y j |
|
|
|
( Y j ,u |
|
|
|
|
||||||
F |
j 1 |
|
|
|
|
|
/ |
j 1 u 1 |
|
|
|
|
|
, |
(4.15) |
|
|
N l |
|
|
N ( M 1 ) |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где l – число значимых коэффициентов в уравнении математической модели (уравнения регрессии), зависимых от выполненного эксперимента.
Если эксперимент состоит из N основных опытов и одной серии параллельных опытов, то
|
|
N |
|
|
? |
|
2 |
|
|
M |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
) |
Y ) |
|
|
|
|
|
||||||||||
|
|
( Y j Y j |
|
|
|
( Y u |
|
|
|
S |
2 |
|
|
|||||||
F |
|
j 1 |
|
|
|
|
|
|
/ |
u 1 |
|
|
|
|
|
|
ОСТ |
, |
(4.16) |
|
|
|
N l |
|
|
( M 1 ) |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
S ВОСПР |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где SОСТ2 – остаточная дисперсия.
Если параллельные опыты отсутствуют, то рассчитывают
|
|
N |
|
Y j ) |
2 |
|
N |
? |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
( Y |
|
|
|
|
( Y j Y j |
|
|
|
|
2 |
|
|
|||
F |
|
j 1 |
|
|
|
/ |
j 1 |
|
|
|
|
|
S Y |
, |
(4.17) |
||
|
|
|
|
|
|
|
|
|
2 |
||||||||
|
|
|
N 1 |
|
|
|
|
( N l ) |
|
|
|
|
S |
||||
|
|
|
|
|
|
|
ОСT |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рассматривая при этом насколько предложенное уравнение лучше описывает рассматриваемую зависимость, чем простейшая модель в форме среднеарифметического представления всей совокупности
N
экспериментальных данных Y const ( Yj ) / N . В этом случае
j 1
исследуемое уравнение адекватно, если расчетное значение F FP , f1 , f 2 .
