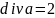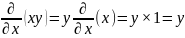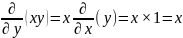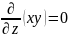- •Список вопросов к зачету по дисциплине «Математическое моделирование экологических процессов» (ммэп)
- •Заменив приращение функции дифференциалом, приближенно вычислить 1,002*2,003.
- •Используем результат первого порядка:
- •Производная второго множителя (2x):
- •Чему равен ротор суммы векторов?
- •Найти минимаксную стратегию первого игрока, если матрица игры имеет вид:
- •Найти нижнюю и верхнюю цену игры для приведенной выше матрицы.
- •Как решается игра, если нижняя и верхняя цены игры равны?
- •Привести пример игры с природой. Какие у природы могут быть стратегии?
- •При замедлении корабля изменение его скорости описывается уравнением:
- •Составить дифференциальное уравнение более высокого порядка методом подстановки для системы уравнений:
Список вопросов к зачету по дисциплине «Математическое моделирование экологических процессов» (ммэп)
Вычислить частные производные первого порядка для функции z = 3x4 + 7y.
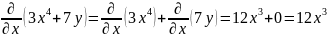
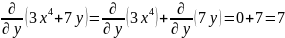
Вычислить частные производные второго порядка для функции z = 2x/y.
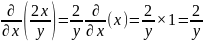
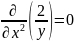
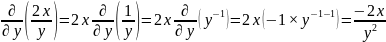
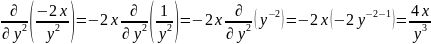
Найти дифференциалы первого и второго порядка для функции z = x2 + y2.
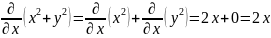
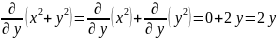
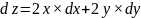
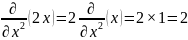
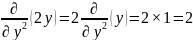
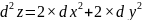
Найти дифференциал df (1,1,1) для функции f (x,y,z) = xy.
Дифференциал функции f(x,y,z) выражается как:
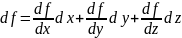
Частные производные:
Подставим эти частные производные в выражение для df:
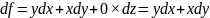
Подставим x и y в формулу:
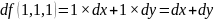
Заменив приращение функции дифференциалом, приближенно вычислить 1,002*2,003.
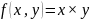
Пусть:
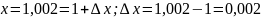
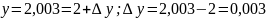
Дифференциал функции равен:
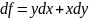
В точке (x,y) = (1,2) частные производные:
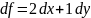
При dx = 0,002 и dy = 0,003:
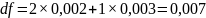
Значение функции в точке (1,2):
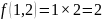
Приближенное значение:
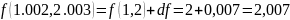
Найти производные первого и второго порядков от сложной функции u = f (x2 + y2 + z2).
Пусть ρ = x2 + y2 + z2, тогда u = f (ρ)
По правилу дифференцирования сложной функции:
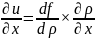
Вычислим
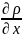 :
:
ρ
= x2
+ y2
+ z2
⟹ 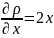
Подставим:
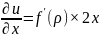
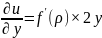
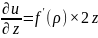
Вторая производная по x:
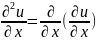
Используем результат первого порядка:
Производная первого множителя (f′(ρ)):
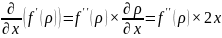
Производная второго множителя (2x):
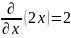
Собираем:
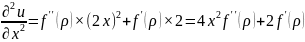
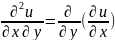
Используем результат первого порядка:
Производная первого множителя (f′(ρ)) по y:
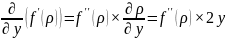
Производная второго множителя (2x):
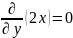
Собираем:
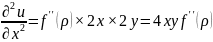
Общий результат:
Частные производные первого порядка:
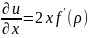
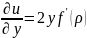
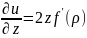
Частные производные второго порядка:
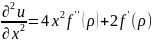
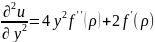
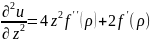
Найти производные первого порядка от сложной функции u = f(t), где t = x + y.
Поскольку t = x + y:
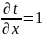
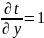
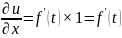
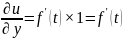
Найти модуль градиента функции z = x2 + y2 в точке М(1, 0).
Градиент функции ∇z определяется как вектор, состоящий из частных производных:
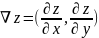
Вычислим частные производные:
Таким образом:
∇z = (2x, 2y)
Подставим координаты M(1,0):
∇z = (2×1; 2×0) = (2,0)
Модуль градиента вычисляется как длина вектора:
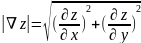
Модуль градиента функции в точке M(1,0):
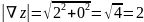
Найти модуль и направление градиента для поля U(x,y) = x2 + 2y в точке О(0,0).
Градиент поля ∇U это вектор частных производных:
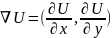
Найдём частные производные:
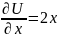
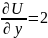
Таким образом:
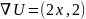
Подставим координаты O(0,0):
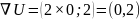
Модуль градиента вычисляется как длина вектора:
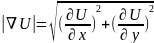
Подставим частные производные:
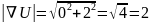
Направление градиента задаётся вектором ∇U. В точке O(0,0) это вектор (0,2). Направление можно описать углом θ между вектором и положительным направлением оси x, вычисленным как:
θ = arctan(вертикальная компонента/горизонтальная компонента)
Для ∇U = (0,2):
θ = arctan(2/0)
Поскольку горизонтальная компонента равна нулю, направление градиента совпадает с положительным направлением оси y, то есть:
θ = 90∘
или
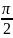 рад.
рад.
Ответ:
Модуль градиента: ∣∇U∣ = 2
Направление градиента: вдоль положительного направления оси y, угол θ = 90∘.
Для векторного поля a = ix +jy найти дивергенцию вектора a в точке М(1,1).
Для вычисления дивергенции векторного поля a, необходимо применить операцию дивергенции, которая определяется как:
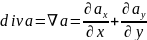
где:
a = ix + jy
ax = x, ay = y
Частные производные:
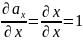
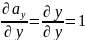
Подставим частные производные в формулу дивергенции:
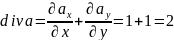
Поскольку дивергенция постоянна и не зависит от координат, в точке M(1,1) она равна: