лабы / метра5

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ИИСТ

отчет

по лабораторной работе №5

по дисциплине «Метрология и измерительная техника»

Тема: «Обработка результатов прямых и косвенных измерений»

Студенты гр. 358		.
		.
Преподаватель		Гелета А.А.

Санкт-Петербург

2025

Цель работы

Ознакомление с методами обработки результатов прямых и косвенных измерений при однократных и многократных измерениях.

Обработка результатов

1. Расчет погрешности измерения сопротивления с помощью цифрового вольтметра:

Результат однократного измерения представим в виде: Uх=U±ΔU, где ΔU - инструментальная погрешность вольтметра, которую найдём по его классу точности по формуле (1.1)

Абсолютная погрешность:

U_х = 6,72 ± 0, 06 В

2. Расчет погрешности измерения сопротивления с помощью аналогового вольтметра:

Определим ток, протекающий через резисторы:

, (2.1)

Относительная погрешность измерения тока будет равна:

(2.2)

где – относительная погрешность измерения напряжения; – относительная погрешность сопротивления образцового резистора.

Откуда следует:

Абсолютную погрешность косвенного измерения тока найдем по формуле:

Результат однократного косвенного измерения тока представим в виде:

Мощность, выделяемая на резисторах , найдем по соотношению:

Относительная погрешность измерения мощности:

где – относительные погрешности измерения напряжения и тока, определенные выше.

Абсолютную погрешность измерения мощности найдем по формуле:

Результат измерения мощности представим в виде:

3. Расчет погрешности измерения сопротивления с помощью измерителя иммитанса:

Найдём оценку математического ожидания в виде среднего арифметического значения результатов наблюдений по формуле (3.1)

где n – число измерений

Найдём оценку среднеквадратического отклонения случайной погрешности измерений по формуле (3.2)

Найдём оценку среднеквадратического отклонения среднего арифметического значения результатов наблюдений по формуле (3.3)

Результаты измерений и вычислений сведены в таблицу 3.1

Доверительный интервал погрешности результата измерений при нормальном законе распределения случайных погрешностей определим по формуле (3.4)

где – коэффициент распределения Стьюдента, соответствующий задаваемой доверительной вероятности P и числу степеней свободы f

Результат измерения напряжения:

4. Обработка результатов многократных косвенных измерений мощности.

Обработка результатов измерения напряжений представлена в пункте 3. Аналогично обработаем результаты измерений напряжения .

Найдем оценку математического ожидания в виде среднего арифметического значения по формуле (3.1):

Для оценки среднеквадратического отклонения случайной погрешности измерений воспользуемся формулой:

Найдем оценку среднеквадратического отклонения среднего арифметического значения результатов наблюдений:

Доверительный интервал погрешности результата измерений при нормальном законе распределения случайных погрешностей определим по формуле (3.4):

Результат измерения напряжения

Определим значения тока:

Найдем среднее арифметическое результатов косвенных измерений тока по формуле:

Определим оценку среднеквадратического отклонения случайной погрешности измерений:

Найдем оценку среднеквадратического отклонения среднего арифметического значения:

Результат измерения мощности при многократном косвенном измерении:

где – среднее значение первого ряда измерений .

Оценку среднеквадратического отклонения вычислим по формуле:

Результат измерения мощности запишем в виде:

где – коэффициент Стьюдента, соответствующий числу степеней свободы .

Эффективное число степеней свободы найдем по формуле:

Выводы: В ходе проведения лабораторной работы мы ознакомились с методами обработки результатов прямых и косвенных измерений при однократных и многократных измерениях. Были практически применены методы оценки случайных погрешностей, включая определение оценки среднеквадратического отклонения и доверительных интервалов.

В рамках работы были выполнены прямые измерения напряжения как однократно (U_х = 6,72 ± 0, 06 В), так и многократно ( ).

Кроме этого, были получены следующие косвенные измерения мощности: однократные и многократные .

Многократные измерения обладают большей точностью и достоверностью.

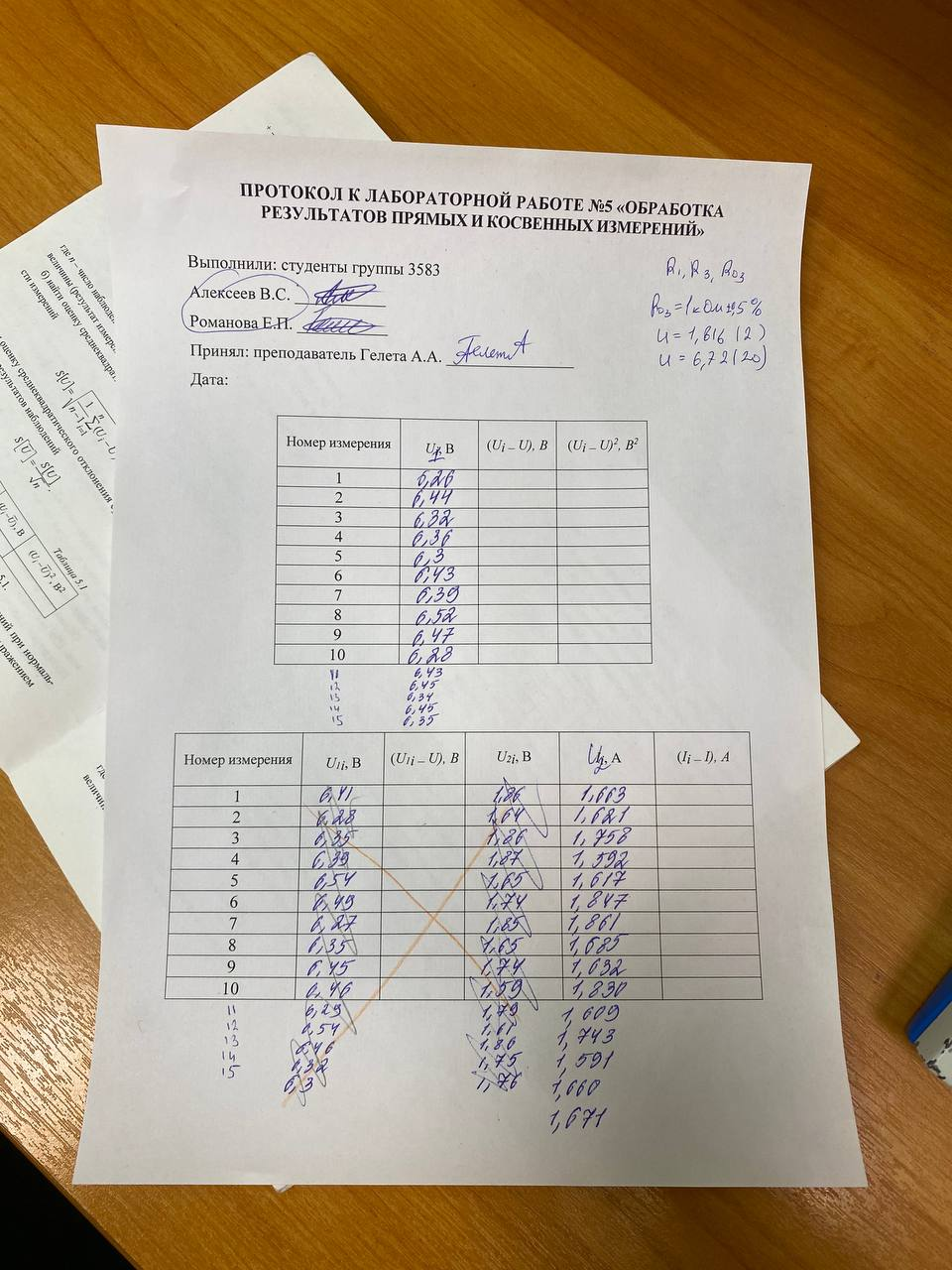
Протокол: