
лабы / метра3
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИИСТ
отчет
по лабораторной работе №3
по дисциплине «Метрология и измерительная техника»
ТЕМА: «Цифровые измерительные приборы»
Студентка гр. 358 |
|
. |
Преподаватель |
|
. |
Санкт-Петербург
2025
Обработка результатов
Статическая характеристика преобразования ЦИП
На вход ЦИП был подключен магазин сопротивлений, предел измерения ЦИП – 2 кОм. При плавном изменении сопротивления магазина следили за изменением показаний и зафиксировали конкретные значения сопротивления магазина R, при которых показания ЦИП Rп меняются на единицу младшего разряда, результаты измерений представлены в таблице 1.
Таблица 1
-
Номер
измерения
Rп, кОм
R, кОм
ΔR
1
0,001
0,98
0,02
2
0,002
1,87
0,13
3
0,003
2,96
0,04
4
0,004
3,97
0,03
5
0,005
4,95
0,05
6
0,006
5,99
0,01
7
0,007
6,99
0,01
8
0,008
7,99
0,01
9
0,009
9,05
-0,05
ΔR=Rп-R – абсолютная погрешность
Приведём пример расчёта абсолютной погрешности
ΔR1 = 1 – 0,98 = 0,02
По полученным значениям построим начальный участок статической характеристики ЦИП в режиме омметра Rп = F(R) (рисунок 1)

Рисунок 1 - Статическая характеристика преобразования ЦИП
Построим график абсолютной погрешности ΔR(R) = F(R) – Fл(R)
(рисунок 2)

Рисунок 2- Абсолютная погрешность ΔR
Абсолютная инструментальная погрешность
Абсолютную инструментальную погрешность определим для 10 точек, равномерно распределённых по выбранному диапазону измерений (2 кОм). Для определения инструментальной погрешности воспользуемся формулой (1). Результаты измерений представлены в таблице 2.

Таблица 2
-
Номер измерения
RпN, кОм
RN, кОм
RиN, кОм
1
0,2
0,199
0,005
2
0,4
0,399
0,005
3
0,6
0,599
0,005
4
0,8
0,799
0,005
5
1
0,998
0,005
6
1,2
1,198
0,0015
7
1,4
1,398
0,0015
8
1,6
1,598
0,0015
9
1,8
1,798
0,0015
10
2
1,997
0,0025
Приведём пример расчёта абсолютной инструментальной погрешности


Определение аддитивной и мультипликативной составляющих погрешности
Для цифровых измерительных приборов погрешность записывается в виде:
 (2)
(2)
где
 -аддитивная
и
-аддитивная
и
 -мультипликативная
составляющие погрешности.
-мультипликативная
составляющие погрешности.
В нашем случае формула имеет вид:
 ,
(3)
,
(3)
Построим
график зависимости
 для определения аддитивной и
мультипликативной составляющих
погрешности ЦИП. Для этого обратимся к
данным из таблицы 2.
для определения аддитивной и
мультипликативной составляющих
погрешности ЦИП. Для этого обратимся к
данным из таблицы 2.
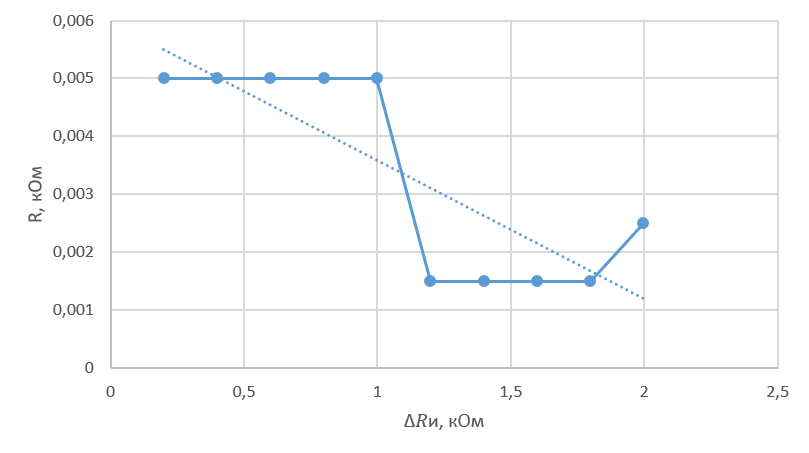
Рисунок 3-Определение аддитивной и мультипликативной составляющей погрешности
Возьмем 1 и 10 измерения из таблицы 2:

Откуда получаем:

Измерение сопротивлений
Для
расчета погрешностей переведем значения
кванта для диапазона измерений
 из Ом в кОм:
из Ом в кОм:
Таблица 3
|
2 кОм |
20 кОм |
200 кОм |
2000 кОм |
2000000 кОм |
, кОм |
0.001 |
0.01 |
0.1 |
1 |
10 |
По
заданию преподавателя были измерены
сопротивления резисторов
 ,
вмонтированных в лабораторный стенд.
Приведем примеры расчетов для оценки
основой погрешности измерения по
формулам:
,
вмонтированных в лабораторный стенд.
Приведем примеры расчетов для оценки
основой погрешности измерения по
формулам:
1)Абсолютная
погрешность измерения
 ,
кОм:
,
кОм:
 ,
(4)
,
(4)

2)Относительная погрешность измерения, %:
 ,
(5)
,
(5)

3)Результат
измерения
 ,
кОм:
,
кОм:
 ,
(6)
,
(6)
 1.14
1.14 0.003
кОм
0.003
кОм
Таблица 4
Номер резистора |
Диапазон измерения, кОм |
Значение кванта для диапазона измерения , кОм |
Показания ЦИП
|
Абсолютная погрешность измерения , кОм |
Относительная погрешность измерения, % |
Результат измерения , кОм |
|
2 |
0.001 |
1.143 |
|
|
1.140 0.003 |
20 |
0.01 |
1.14 |
0.01228 |
1.08 |
1.140 0.012 |
|
200 |
0.1 |
1.1 |
0.1022 |
9.29 |
1.10 0.10 |
|
2000 |
1 |
1 |
1.002 |
100 |
1 1 |
|
2000000 |
10 |
0 |
10 |
- |
0 10 |
|
|
2 |
0.001 |
- |
- |
- |
- |
20 |
0.01 |
8.12 |
0.02624 |
0.32 |
8.120 0.026 |
|
200 |
0.1 |
8.1 |
0.1162 |
1.43 |
8.10 0.12 |
|
2000 |
1 |
8 |
1.016 |
12.7 |
8 1 |
|
2000000 |
10 |
0 |
10 |
- |
0 10 |
|
|
2 |
0.001 |
- |
- |
- |
- |
20 |
0.01 |
- |
- |
- |
- |
|
200 |
0.1 |
131.1 |
0.3622 |
0.28 |
131.1 0.4 |
|
2000 |
1 |
130 |
1.26 |
0.97 |
130,0 1.3 |
|
2000000 |
10 |
0.13 |
10.65 |
8.19 |
(0.13 0.01) |
Вывод: В ходе проведение лабораторной работы были исследованы и применены для измерения физических величин метрологические характеристики цифровых приборов, а именно статическая характеристика, абсолютная основная и абсолютная инструментальная погрешности, аддитивная и мультипликативные составляющие погрешности. Построенный начальный участок статической характеристики ЦИП в режиме омметра совпадает с теоретическим видом графика, что свидетельствует о корректно снятых показаниях прибора.
В ходе обработки результатов был построен
график зависимости
,
благодаря которому были найдены
аддитивная и мультипликативная
составляющие, равные
 и
и
 .
Аддитивная составляющая не зависит от
и меняется малозначительно, что можно
заметить на рисунке 3, а мультипликативная
- проходит под острым углом.
.
Аддитивная составляющая не зависит от
и меняется малозначительно, что можно
заметить на рисунке 3, а мультипликативная
- проходит под острым углом.
Также по заданию преподавателя были измерены сопротивления резисторов и оценена основная погрешность измерения, представленная в таблице 4. Относительная погрешность измерения менялась от 0.28% до 100 %, что говорит нам о необходимости выбора наименьшего диапазона из возможных для более точных значений. Например, для резистора мы не можем взять диапазон измерений 2 кОм и 20 кОм, так как в целом не имеем в них показаний ЦИП, следовательно, берем 200 кОм. И действительно, при 200 кОм относительная погрешность составляет 0.28 %, а при 2000000 кОм – 8.19%, что подтверждает вышесказанное.
Протокол:
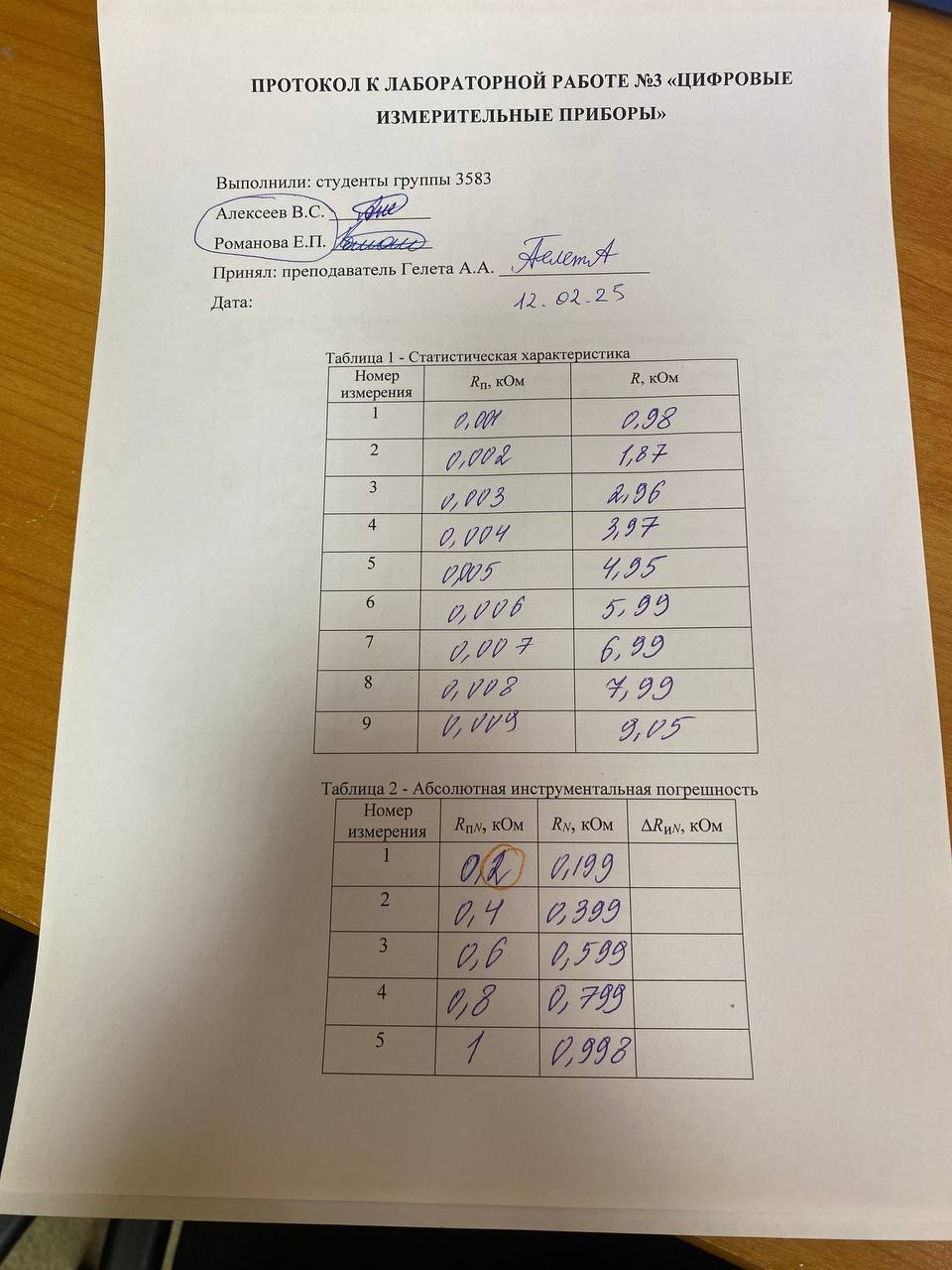
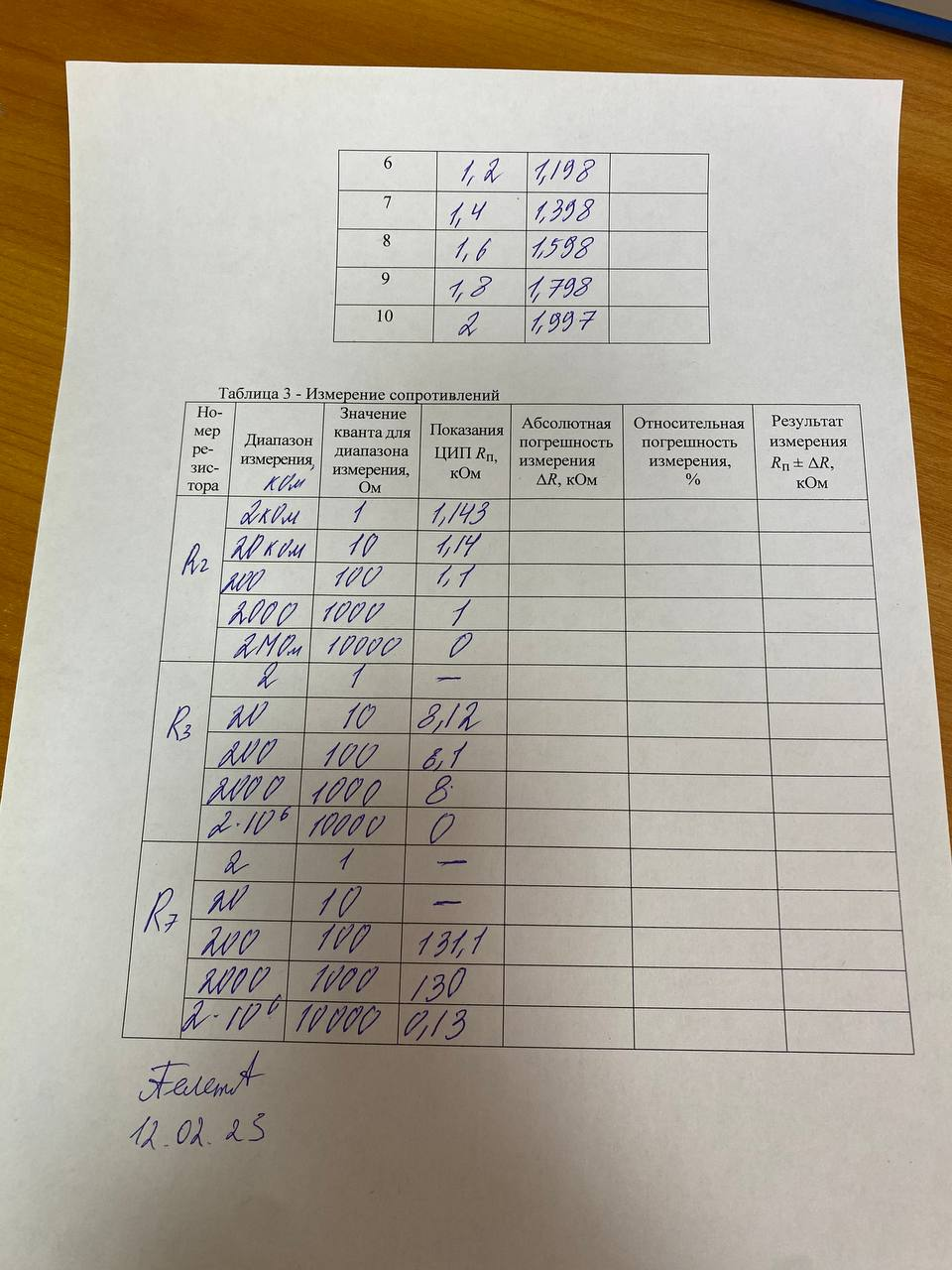


 ,
кОм
,
кОм




