идз / материалкаидз1

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физической химии

отчет

по индивидуальному домашнему заданию №1

по дисциплине «Материаловедение»

ТЕМА: СИММЕТРИЯ КРИСТАЛЛОВ

Вариант №2

Студентка гр. 358		.
Преподаватель		Карпов О. Н.

Санкт-Петербург

2025

Цели работы: Научиться качественно и количественно определять

симметрию кристаллов на моделях, которые соответствуют формам реальных кристаллов минералов, металлов и других кристаллических веществ.

Основные теоретические положения

Кристаллами называются твердые тела с упорядоченным внутренним строением на уровне атомов и молекул, т.е. тела, обладающие трехмерно-периодической пространственной атомной структурой, и имеющие при определенных условиях образования форму многогранников.

Кристаллический многогранник – это многогранник, в котором равные части (грани, ребра) расположены так, что он совмещается целиком сам с собой при помощи некоторых операций симметрических преобразований (такое преобразование, в результате которого все равные части фигуры совмещаются друг с другом, и фигура совмещается сама с собой).

Элементы симметрии – это геометрические образы симметрических

преобразований. Симметрия кристаллов выявляется с помощью элементов

симметрии:

• центра симметрии (инверсии),

• плоскостей симметрии,

• осей симметрии.

Центр симметрии (инверсии) связывает противоположные инверсионно

равные (или обращено равные) части кристалла. Он совпадает с геометрическим центром кристалла. Обозначается буквой С (по символике Бравэ). Определяют наличие С у многогранников по следующему признаку: если каждой грани многогранника соответствует равная и параллельная грань, то такой многогранник имеет центр инверсии.

Осью симметрии называется прямая линия, при повороте вокруг которой на некоторый определённый угол α, фигура совмещается сама с собой. Обозначается в учебной символике - символике О.Браве – Ln. Число n, показывающее сколько раз элементарный угол поворота оси содержится в 360°, называется порядком оси. n – целое число (n = 360°/α n=1,2,3,4,6).

Плоскостью симметрии называется плоскость, которая делит фигуру на две равные части, расположенные друг относительно друга как предмет и его зеркальное отражение. Обозначается в символике О.Браве - P.

Вид симметрии - это полная совокупность элементов симметрии какого-либо кристалла.

Сингония (равноугольность) - это группа видов симметрии, объединенная либо одной главной осью симметрии, определяющей форму поперечного сечения кристалла, либо особенностью расположения координатных осей при установке кристалла.

Категория - это группа сингоний с характерным набором осей симметрии:

• Высшая категория характеризуется обязательным наличием в каждом виде симметрии 4L3 в сочетании с осями L4 и L2. Высшая категория включает в себя только одну, кубическую сингонию.

• Средняя категория характеризуется наличием одной оси симметрии высшего порядка в сочетании с прочими элементами симметрии. К средней категории относятся тригональная, тетрагональная и гексагональная сингонии.

• Низшая категория объединяет триклинную, моноклинную и ромбическую сингонии, во всех видах симметрии, которых отсутствуют оси симметрии высшего порядка.

Ход работы

Кристаллы, полученные у преподавателя для варианта №2:

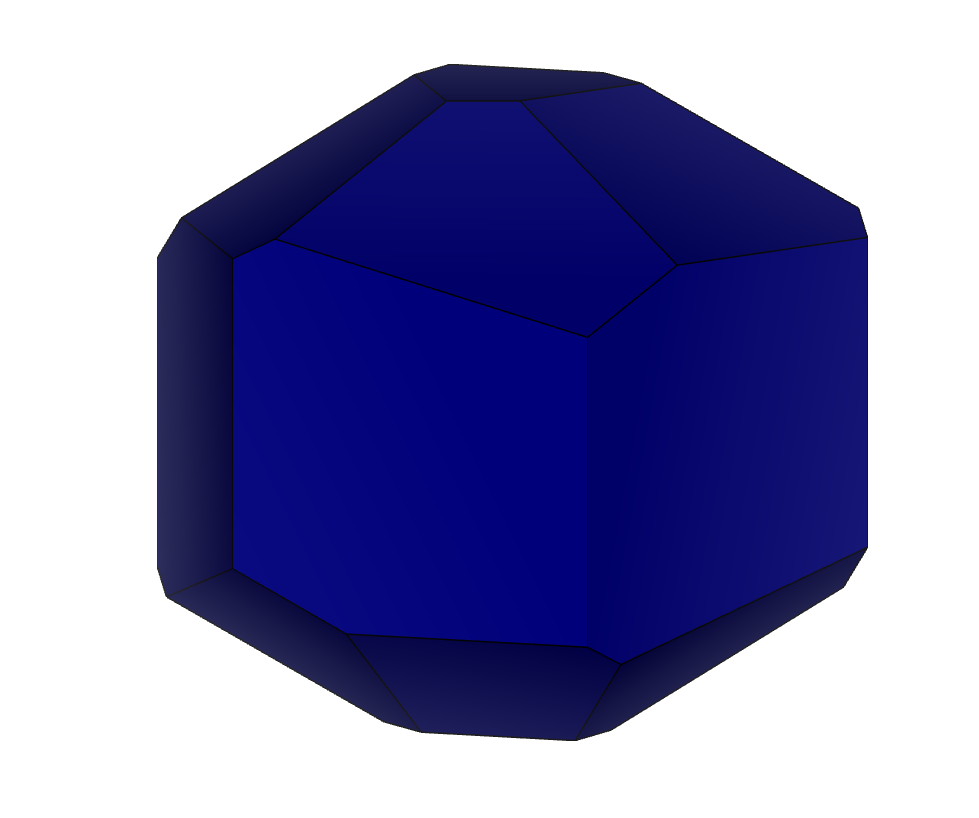
Рисунок 1 – кристалл 2-1

Рисунок 2 – кристалл 2-2

Приведем проекции кристаллов для их описания:

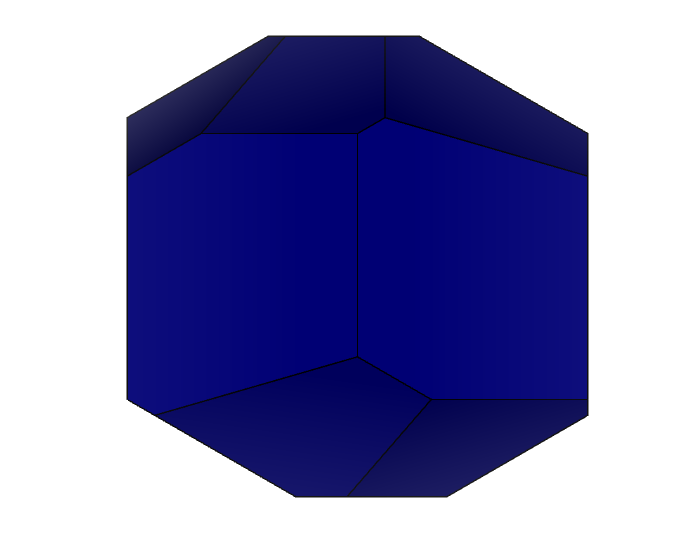
Рисунок 3 – проекции кристалла 2-1

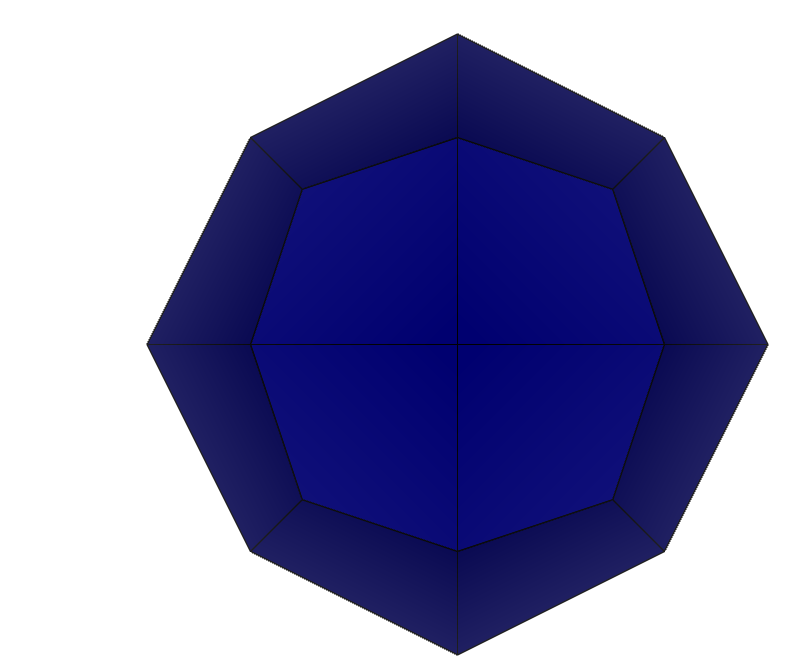
Рисунок 4 – проекции кристалла 2-2

1.Определение центра симметрии

Для определения симметрии найдем все возможные оси симметрии. Повернем модель кристалла в пространстве таким образом, чтобы исследуемая грань стала «подсвеченной»:

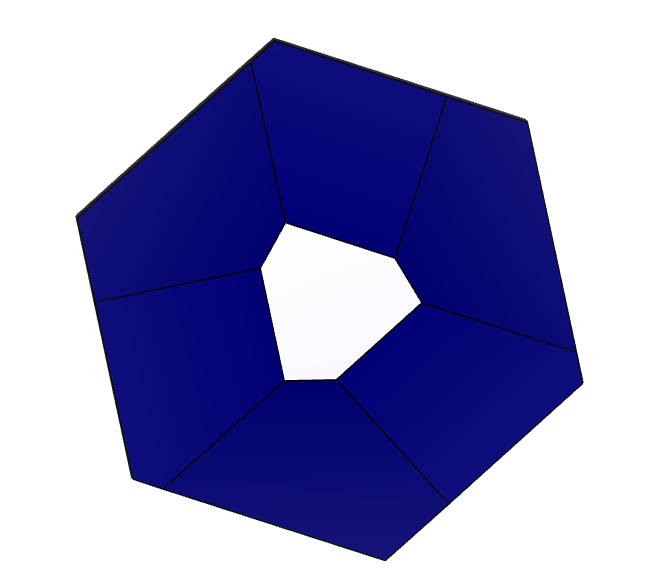
Рисунок 5 – Модель кристалла 2-1 с «подсвеченной» гранью.

Произведем поворот кристалла вдоль осей X, Y, Z. Выделим две грани разной формы:

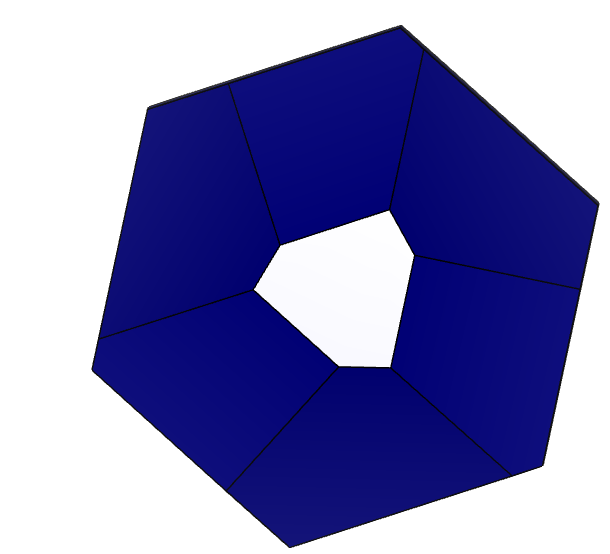
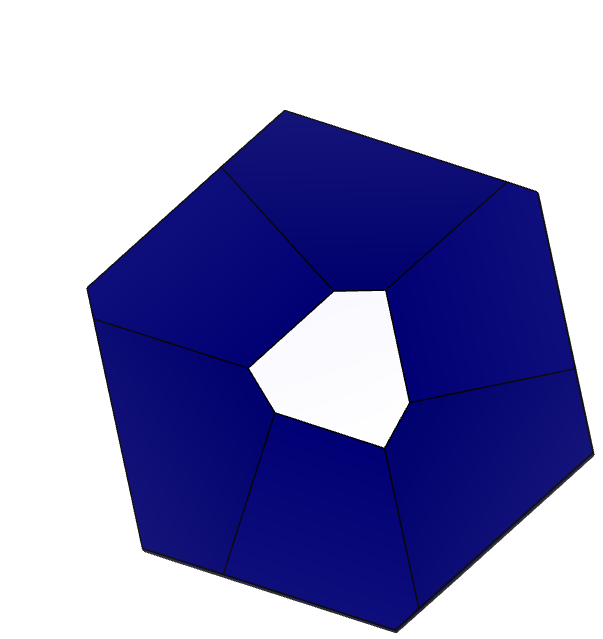
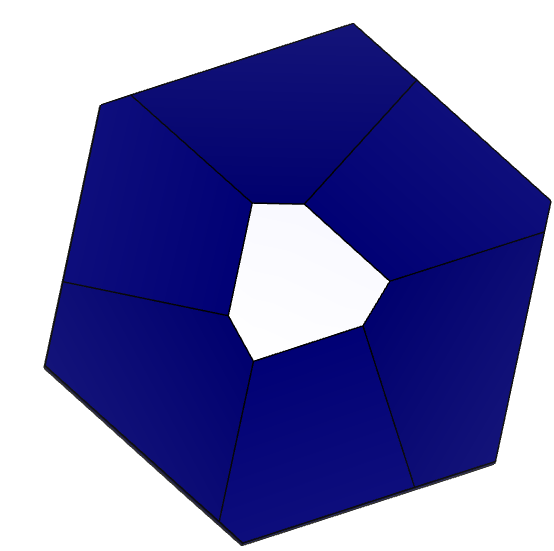
Рисунок 6 – Результат поворота первой грани около осей 1) – X, 2) – Y, 3) – Z.

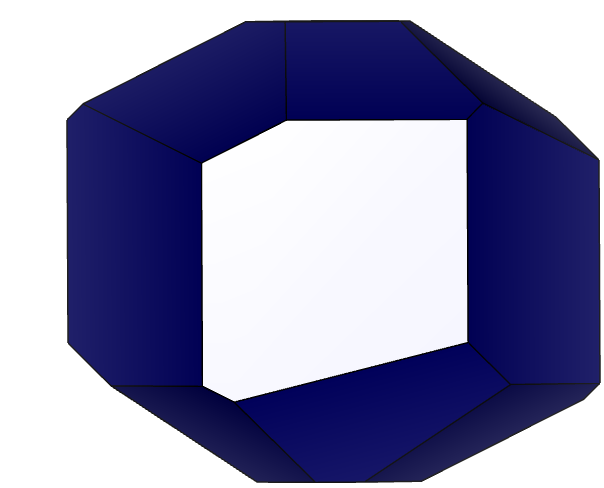
Рисунок 7 – Результат поворота второй грани около осей 1) – X, 2) – Y, 3) – Z.

Следовательно, можем сделать вывод, что кристалл 2-1 имеет центр симметрии.

Аналогично рассмотрим кристалл 2-2:

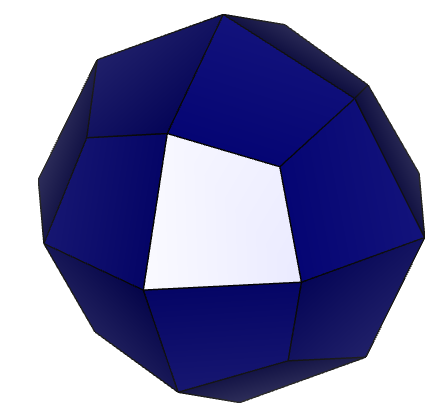
Рисунок 8 – Модель кристалла 2-1 с «подсвеченной» гранью.

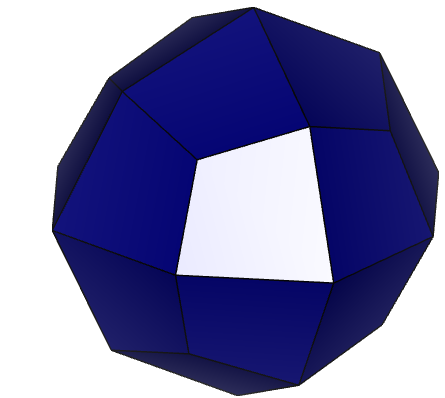
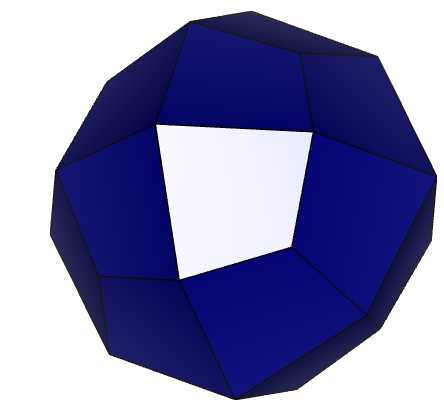
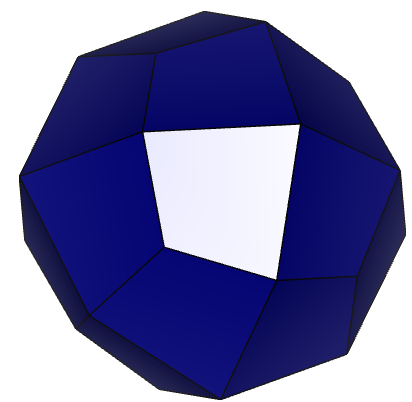
Рисунок 9 – Результат поворота первой грани около осей 1) – X, 2) – Y, 3) – Z.

Остальные грани кристалла 2-2 аналогичны. Можем сделать вывод, что данный кристалл имеет центр симметрии.

2.Поиск осей симметрии

Для поиска осей симметрии рассмотрим кристалл 2-1 сверху. Применим операцию поворота вдоль оси на 120 градусов и убедимся, что фигура совмещается сама с собой:

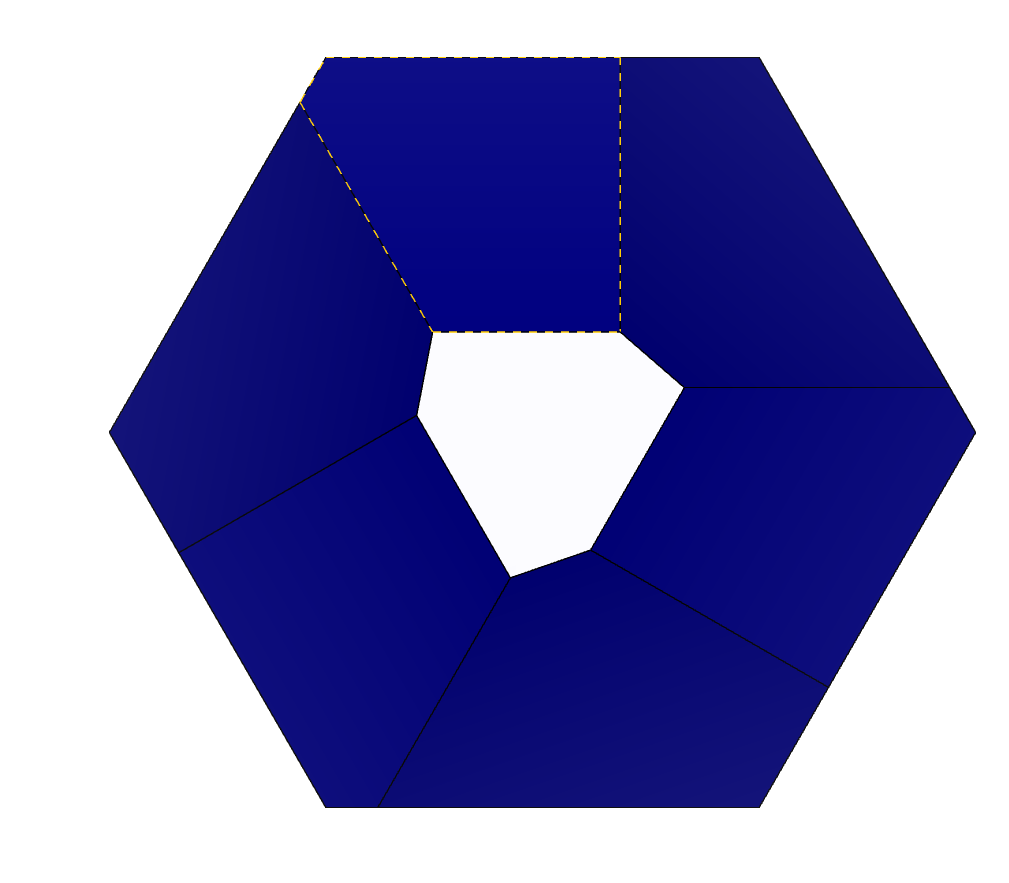
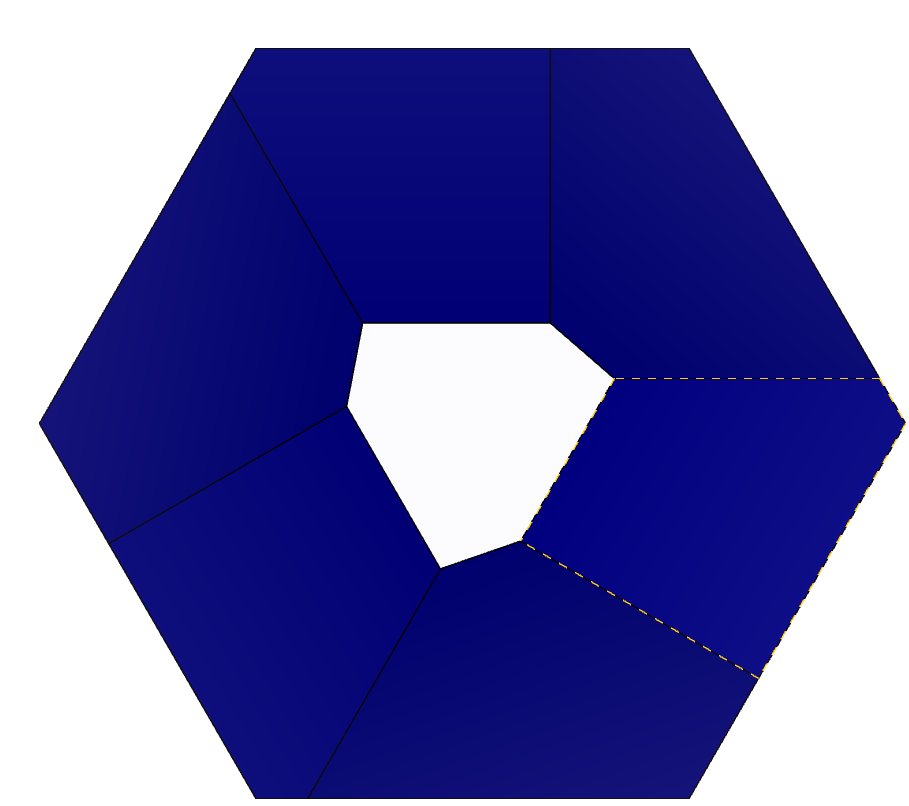
Рисунок 10 – Вид сверху кристалла 2-1: 1) исходное состояние 2) поворот вдоль оси на 120 градусов.

Таким образом, кристалл 2-1 имеет лишь одну ось симметрии с углом поворота 120 градусов.

Рассмотрим кристалл 2-2. Применим операцию поворота вдоль оси на 90 градусов и убедимся, что фигура совмещается сама с собой. Оси симметрии с углом 90 также рассматриваются при видах спереди и сбоку.

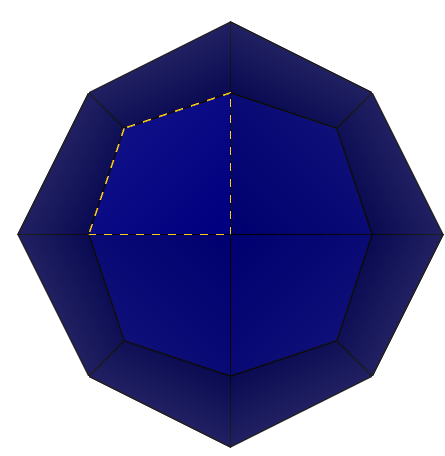
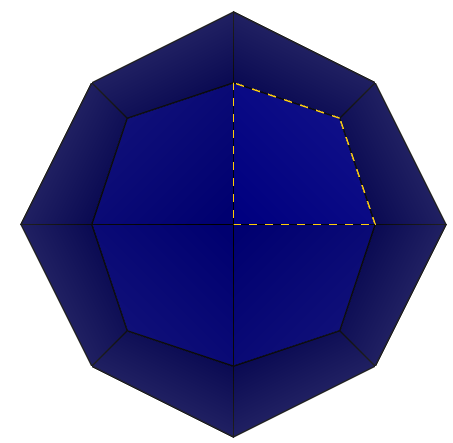
Рисунок 11 – Вид сверху кристалла 2-2: 1) исходное состояние 2) поворот вдоль оси на 90 градусов.

При виде сбоку применим операцию поворота вдоль оси на 180 градусов и убедимся, что фигура совмещается сама с собой.

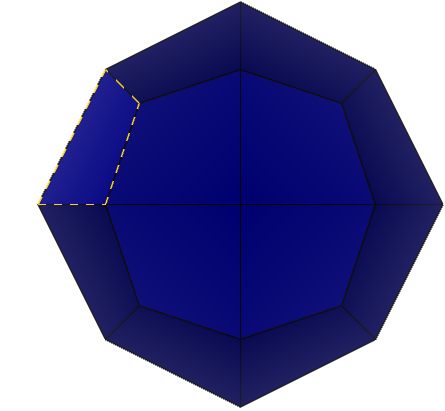
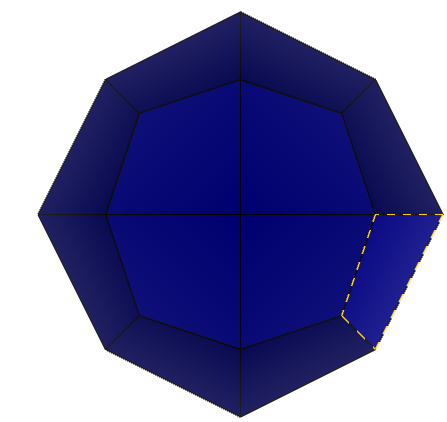
Рисунок 12 – Вид сбоку кристалла 2-2: 1) исходное состояние 2) поворот вдоль оси на 180 градусов.

Вид с угла на кристалл 2-2. Применим операцию поворота вдоль оси на 120 градусов и убедимся, что фигура совмещается сама с собой. Аналогично оси симметрии с углом поворота 120 будут с каждого угла. Всего получилось 4.

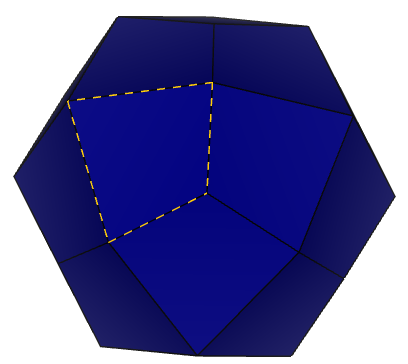
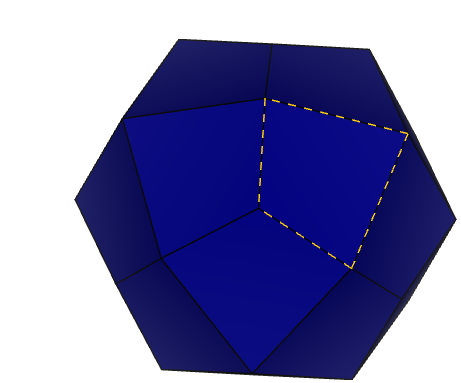
Рисунок 13 – Вид с угла 2-2: 1) исходное состояние 2) поворот вдоль оси на 120 градусов.

Таким образом, кристалл 2-2 имеет: 3 оси симметрии 4-ого порядка, 4 оси симметрии 3-его порядка и 6 осей симметрии 2-ого порядка.

3.Поиск плоскостей симметрии

Кристалл 2-1 не имеет плоскостей симметрии.

Кристалл 2-2 имеет несколько плоскостей симметрии. Можем провести 3 из них вдоль основных осей X, Y, Z. Также 6 будет проходить вдоль диагональных ребер. Итого мы получили 9 плоскостей симметрии.

Рисунок 14 – Демонстрация плоскостей симметрии кристалла 2-2.

Обработка данных

Запишем кристаллографическую формулу кристаллов согласно символике Браве:

Номер варианта	Оси симметрии и их порядок				Плоскости симметрии	Центр симметрии	Кристаллографическая формула	Сингония и вид (класс) симметрии
	2	3	4	6
2-1	-	1	-	-	нет	есть		Тригональная центральная
2-2	6	4	3	-	9	есть		Кубическая планаксиальная

По найденным формулам кристаллов 2-1 и 2-2 приведем примеры минералов:

Рисунок 15 – (пример минерала для 2-1)

Рисунок 16 – Гранат (пример минерала для 2-2)

Выводы: В ходе выполнения данного индивидуального домашнего задания были освоены навыки качественного и количественного определения симметрии кристаллов на моделях, которые соответствуют формам реальных кристаллов минералов, металлов и других кристаллических веществ.

Также были определены сингония и вид симметрии для рассматриваемых моделей: 2-1 - тригональная центральная; 2-2 - кубическая планаксиальная.