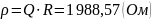тоэ 7 лаба готовая
.docxМИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В. И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра ТОЭ
Отчет
по лабораторной работе №7
по дисциплине «Теоретические основы электротехники»
Тема: ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ ЯВЛЕНИЙ В ПРОСТЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Санкт-Петербург
2025
Цель: исследование резонанса и АЧХ последовательного колебательного контура.
Резонанс – это такое состояние RLC-цепи в установившемся синусоидальном режиме, при котором напряжение и ток на входе цепи совпадают по фазе.
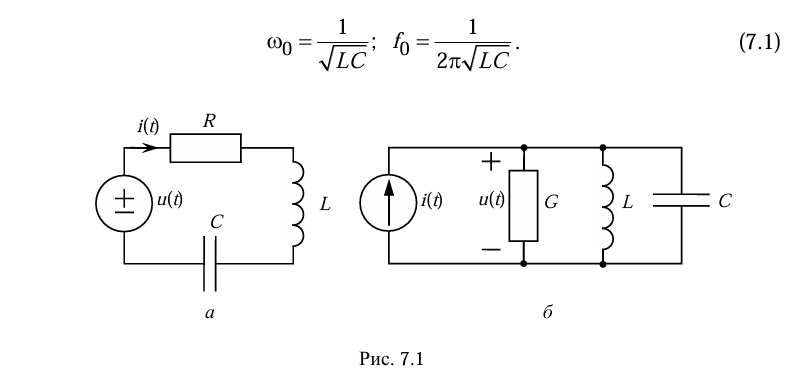
Схемы исследуемых цепей приведены на рис. 7.1. Резонанс в цепи на рис. 7.1, а называют резонансом напряжений, а цепь – последовательным контуром; резонанс в цепи на рис. 7.1, б – резонансом токов, а цепь – параллельным контуром.
При
резонансе вещественными становятся
комплексное сопротивление последовательной
 и, соответственно, комплексная проводимость
параллельной цепи
и, соответственно, комплексная проводимость
параллельной цепи
 Отсюда резонансная частота приведенных
на рис 7.1 а, б цепей:
Отсюда резонансная частота приведенных
на рис 7.1 а, б цепей:

При резонансе модуль проводимости цепи на рис 7.1, а становится максимальным:
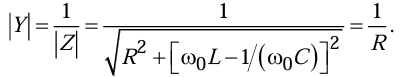
Это
значит, что при
 максимальным будет ток:
максимальным будет ток:
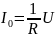
Напряжения на емкости и индуктивности в цепи на рис. 7.1, а при резонансе компенсируют друг друга и могут быть во много раз больше напряжения источника. Отношение действующего значения напряжения любого из реактивных элементов к напряжению источника при называют добротностью Q последовательного контура:

где

Если
в режиме резонанса измерены напряжения
на входе U и на конденсаторе
 ,
ток
,
ток
 и резонансная частота
и резонансная частота
 ,
то из приведенных соотношений можно
определить все параметры последовательного
контура: сопротивление R из (7.2), добротность
Q и характеристическое сопротивление
ρ из (7.3), а емкость и индуктивность из
(7.1) и (7.3):
,
то из приведенных соотношений можно
определить все параметры последовательного
контура: сопротивление R из (7.2), добротность
Q и характеристическое сопротивление
ρ из (7.3), а емкость и индуктивность из
(7.1) и (7.3):

Параллельный RLC-контур на рис. 7.1, б дуален последовательному. При резонансе токов максимальным становится модуль его комплексного сопротивления:
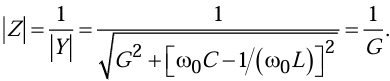
Это значит, что при максимальным будет напряжение на входе цепи:
![]()
Токи, протекающие через индуктивность и емкость в цепи на рис. 7.1, б, при резонансе компенсируют друг друга и могут во много раз быть больше тока источника. Отношение действующего значения тока любого из реактивных элементов к току источника при называют добротностью параллельного контура:

Если
в режиме резонанса измерены входной
ток I и ток конденсатора
 ,
напряжение
,
напряжение
 и
резонансная частота
,
то из (7.5) можно определить G, из (7.6) Q
и ρ, а из (7.4) – L
и C.
и
резонансная частота
,
то из (7.5) можно определить G, из (7.6) Q
и ρ, а из (7.4) – L
и C.
При отклонении частоты от резонансной реактивное сопротивление последовательного контура и реактивная проводимость параллельного не равны нулю, поэтому ток первого и напряжение второго уменьшаются.
АЧХ (резонансное кривая) последовательного контура есть зависимость модуля проводимости от частоты:
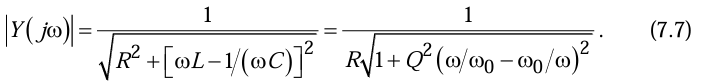
Для параллельного контура, дуально, АЧХ – это зависимость модуля со противления от частоты:

«Острота» резонансной кривой определяет частотную избирательность цепи. По АЧХ можно определить добротность контура. Она равна отношению к полосе пропускания f, измеренной по уровню 0,707 от максимума АЧХ:
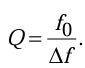
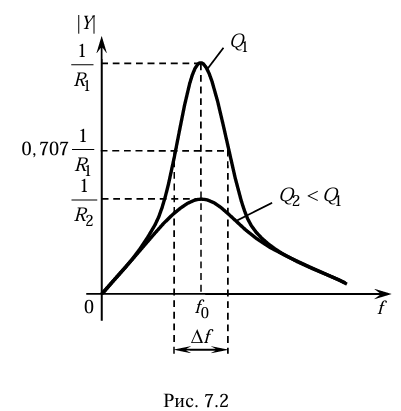
Примерный вид АЧХ, построенных по выражению 7.7 при различных значениях R, представлен на рис 7.2
Обработка результатов эксперимента

Рис 7.1.1 Схема цепи с малыми потерями
 Исследование
резонанса напряжений и АЧХ контура с
малыми потерями
Исследование
резонанса напряжений и АЧХ контура с
малыми потерями





Измеряют |
Вычисляют |
|||||||
|
|
|
|
|
|
|
|
|
2,000 |
11,83 |
4,5 |
34,1 |
169,06 |
17,05 |
2882,50 |
0,1 |
0,012 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
Рис
7.1.2 АЧХ последовательного контура с
малыми потерями

Исследование резонанса напряжений и АЧХ контура с большими потерями
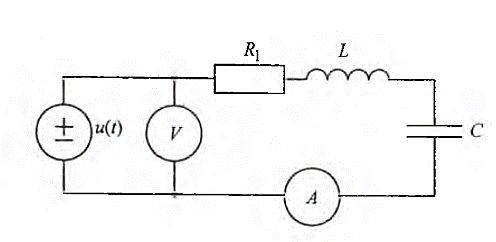
Рис
7.2.1 Схема последовательного контура с
большими потерями
Измеряют |
Вычисляют |
||||||||
|
|
|
|
|
|
|
|
|
|
2,00 |
3,09 |
3,70 |
9,82 |
647,25 |
4,91 |
3177,99 |
0,14 |
0,0135 |
|
|
|
|
|
|
11623,89 |
1,85 |
0,21 |
2,08 |
|
13948,67 |
2,22 |
0,44 |
2,90 |
|
16273,45 |
2,59 |
0,71 |
4,16 |
|
18598,23 |
2,96 |
0,95 |
6,37 |
|
20923,01 |
3,33 |
1,03 |
10,73 |
|
23247,79 |
3,70 |
1,17 |
15,45 |
|
25572,56 |
4,07 |
1,28 |
11,27 |
|
27897,34 |
4,44 |
1,33 |
7,50 |
|
30222,12 |
4,81 |
1,33 |
5,53 |
|
32546,90 |
5,18 |
1,32 |
4,40 |
|
34871,68 |
5,55 |
1,27 |
3,67 |
Рис
7.2.2 АЧХ последовательного контура с
большими потерями потерями

Исследование влияния ёмкости на характеристики контура
Рис
7.3.1 Схема последовательного контура с
дополнительной емкостью

Измеряют |
Вычисляют |
||||||||
|
|
|
|
|
|
|
|
|
|
2,000 |
3,500 |
2,000 |
6,960 |
571,43 |
3,48 |
1988,57 |
0,158 |
0,04 |
|
|
|
|
|
0,00124
|
6283,19 |
1 |
0,910 |
3,29 |
|
7539,82 |
1,2 |
1,330 |
4,55 |
|
8796,46 |
1,4 |
1,730 |
6,42 |
|
10053,10 |
1,6 |
2,630 |
9,42 |
|
11309,73 |
1,8 |
3,200 |
14,10 |
|
12566,37 |
2 |
3,500 |
17,50 |
|
13823,01 |
2,2 |
2,780 |
14,58 |
|
15079,64 |
2,4 |
2,440 |
10,79 |
|
16336,28 |
2,6 |
2,020 |
8,33 |
|
17592,92 |
2,8 |
1,650 |
6,76 |
|
18849,56 |
3 |
1,380 |
5,70 |

Рис
7.2.2 АЧХ последовательного контура с
большими потерями потерями
Вывод: в ходе лабораторной работы был исследован резонанс в последовательном RLC-контуре. Было экспериментально подтверждено, что в последовательном RLC-контуре при определенной частоте (резонансной частоте) наблюдается резкое увеличение амплитуды тока. Это происходит из-за того, что на резонансной частоте реактивное сопротивление индуктивности и емкости компенсируют друг друга, и полное сопротивление контура становится минимальным. Исследовано влияние величины активного сопротивления и дополнительной емкости на характеристики резонанса. Также была посчитана добротность последовательного контура по экспериментальным значениям и по графику АЧХ. Расхождения значений обусловлены аппроксимацией графика.




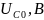




















 0,0011
0,0011