тоэ 3 лаба идеал
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В. И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №3
по дисциплине «Теоретические основы электротехники»
Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ
В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Санкт-Петербург
2025
Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.
Обработка результатов:
3.2.1. Исследование свободных процессов в цепи первого порядка.
1)Расчет
СЧ по теоретическим данным
C = 0,02 мкФ R = 5кОм,
Гц
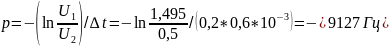
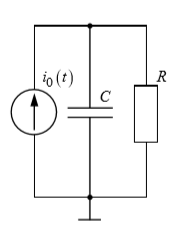
Рис
3.2.1.1 Схема
цепи
Полученное экспериментальное значение отличается от экспериментального с погрешностью примерно 9%
Рис
3.2.1.2 Осциллограмма цепи 1 порядка
Рис
3.2.1.3 СЧ на комплексной плоскости Цепи
1 порядка
3.2.2. Исследование свободных процессов в цепи второго порядка.
3.2.2.1 Колебательный режим
1)Расчет СЧ по теоретическим данным
С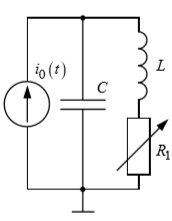
=
0,02 мкФ
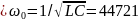
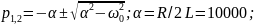
Рис
3.2.2 Схема
цепи
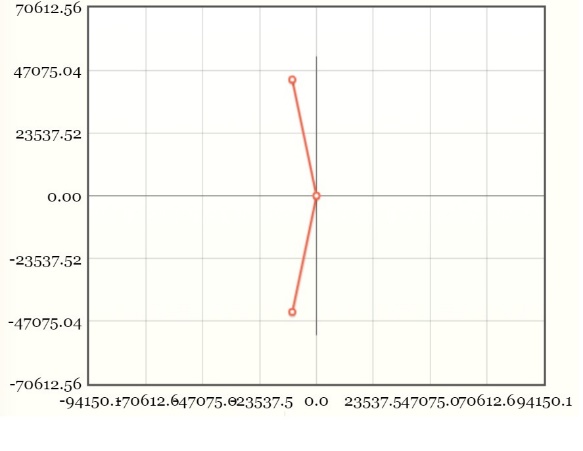
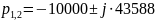
Рис
3.2.2.1.2 СЧ
на комплексной плоскости
2)Расчет СЧ по изображению осциллограммы
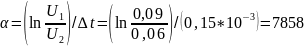
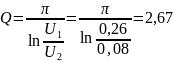
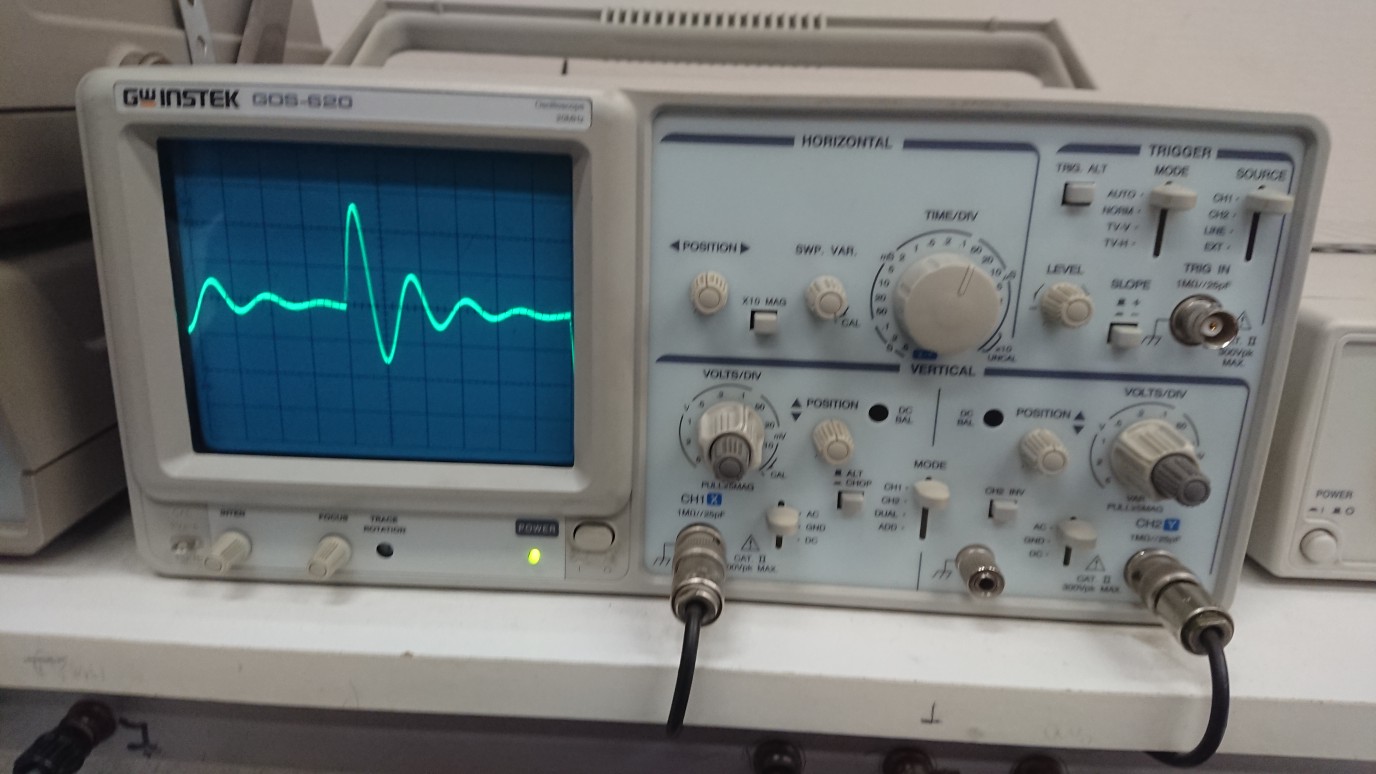
Рис
3.2.2.1.3 осциллограмма
цепи 2 порядка
3.2.2.2 Апериодический режим
С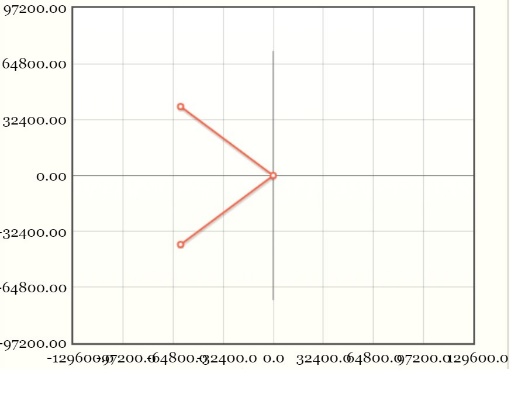
хема
цепи представлена на рис 3.2.2
1)Расчет по теоретическим значения
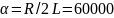
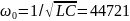
Рис
3.2.2.2.1 СЧ
на комплексной плоскости
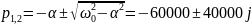
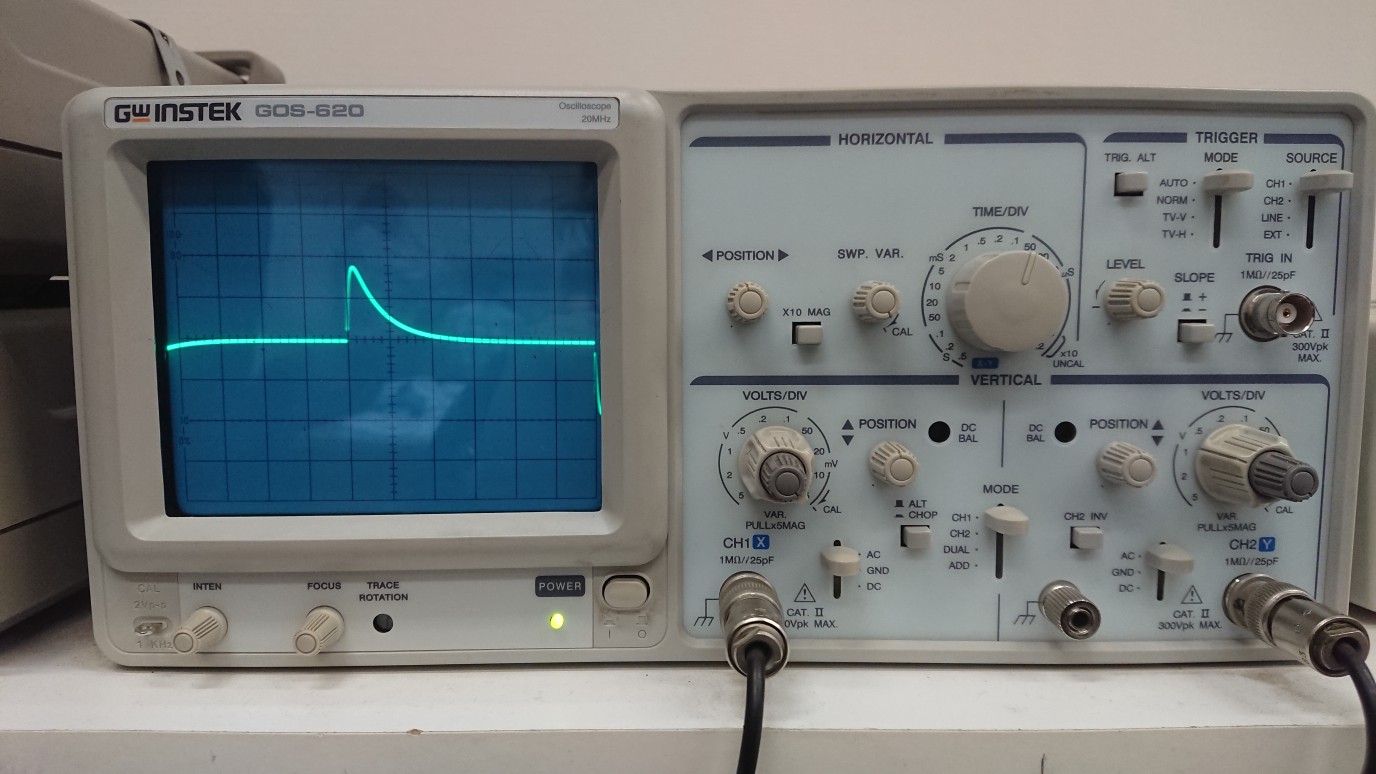
Рис
3.2.2.2.2 осциллограмма цепи 2 порядка
(апериодический режим)
3.2.2.3 Критический режим при R1 = 1,5 кОм
C
=0,02
мкФ
=
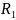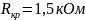
L=25 мГн
1)Расчет по теоретическим данным
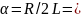30000
Рис
3.2.2.3.1 СЧ
на комплексной плоскости
2)Расчет по изображению осциллограммы
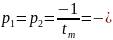33333
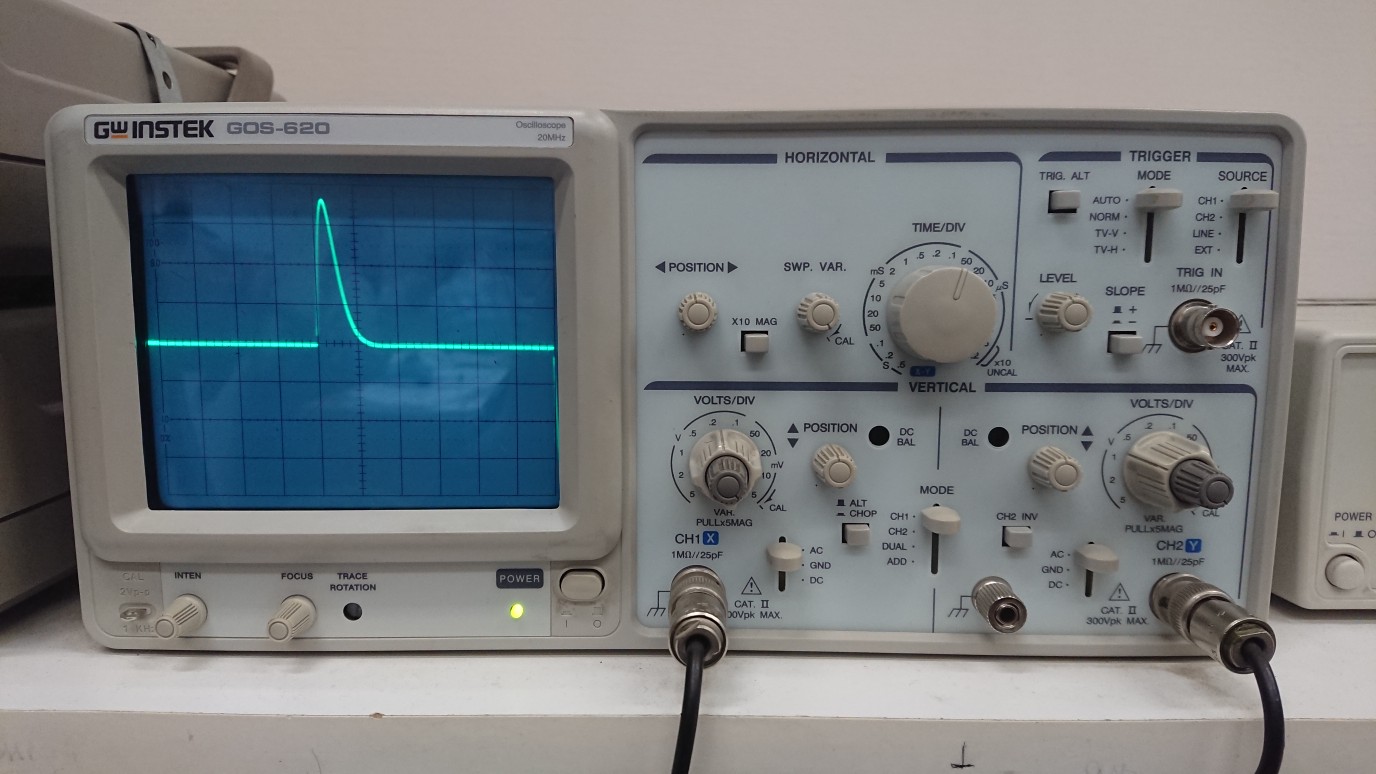
Рис
3.2.2.3.2
осциллограмма
цепи 2 порядка (критический
режим)
3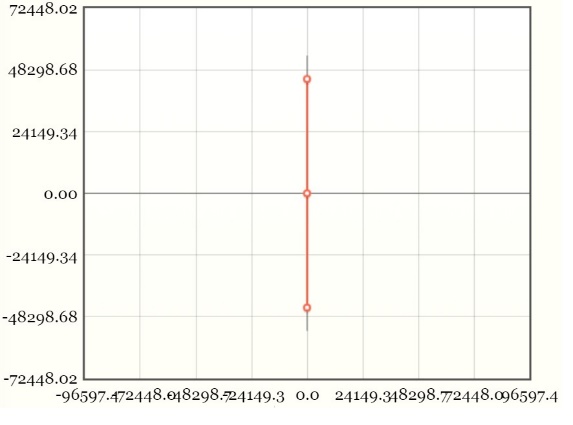
.2.2.4
Незатухающий режим (R=0)
L=25 мГн
Рис
3.2.2.4.1 СЧ
на комплексной плоскости
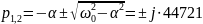
Расчет добротности согласно изображению осциллограммы
32,76
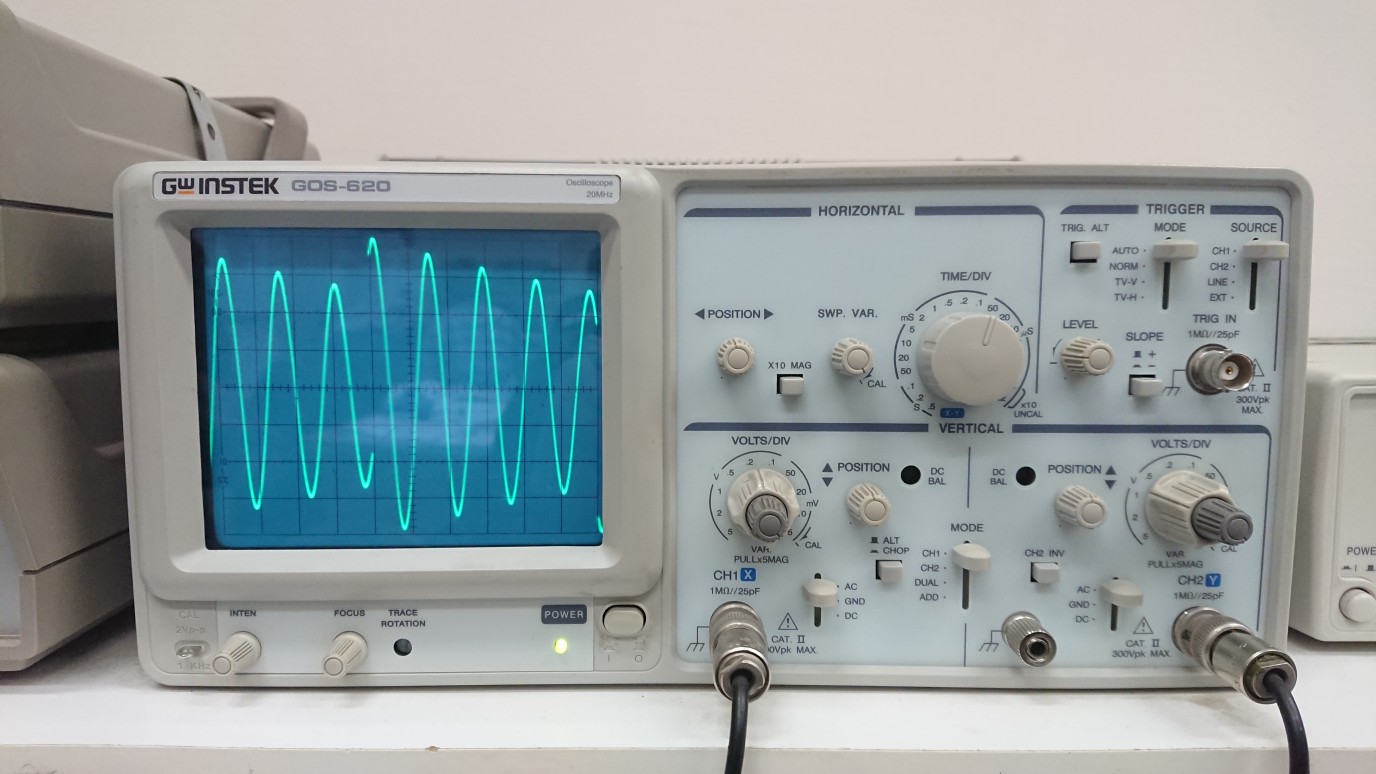
Рис
3.2.2.4.2 осциллограмма цепи 2 порядка
(незатухающий режим)
3.2.3 Исследование свободных процессов в цепи третьего порядка.
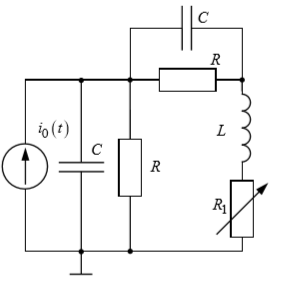
C=0,02 мкФ
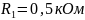
L=25 мГн
Расчет СЧ по теоретическим данным
Рис
3.2.3 Схема
цепи
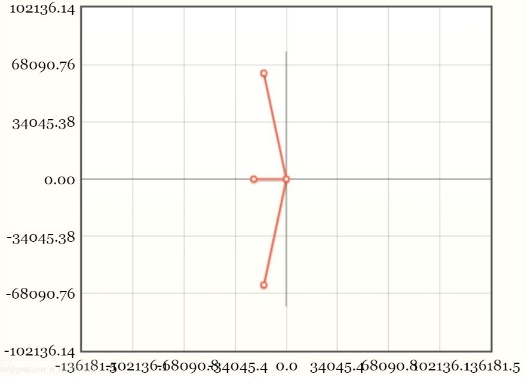
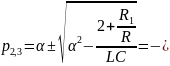5000
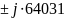
Рис
3.2.3.1 СЧ
на комплексной плоскости
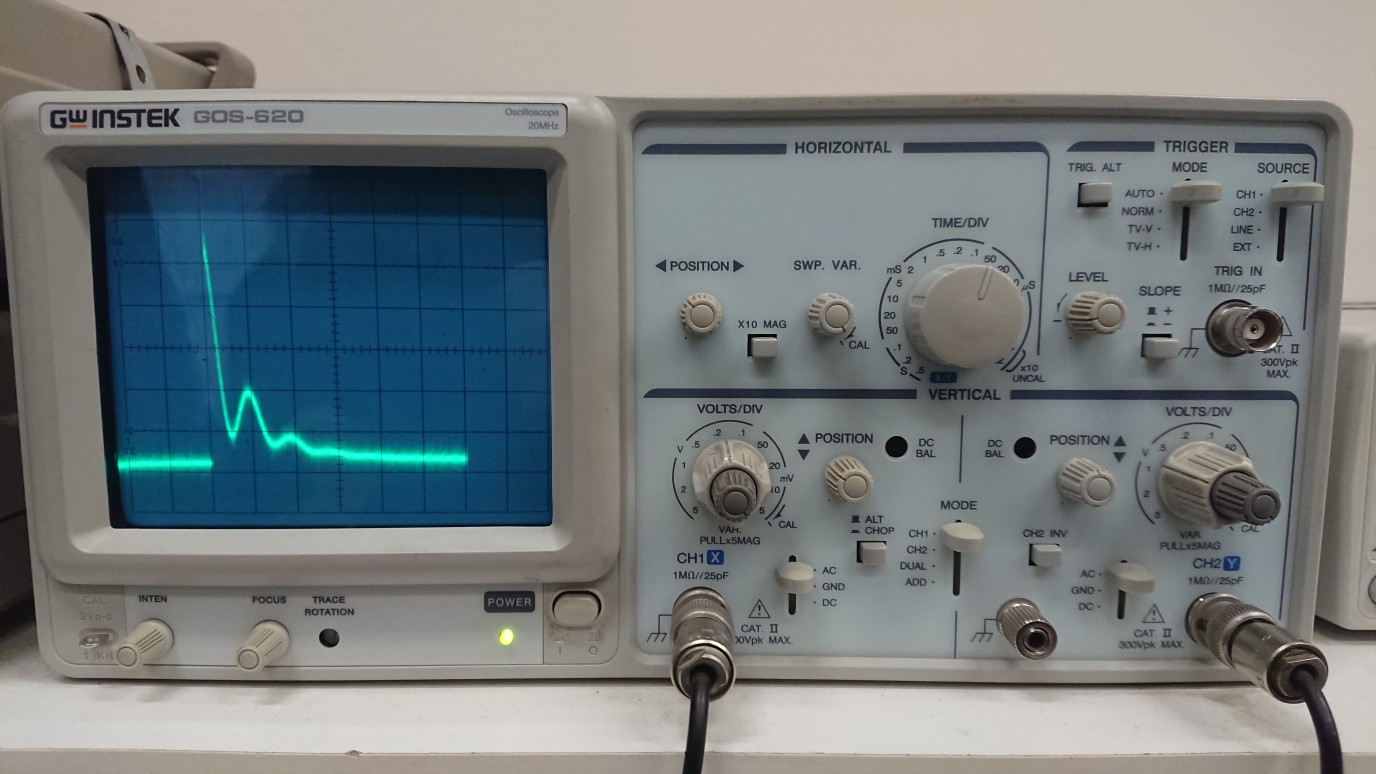
Рис 3.2.3.2 осциллограмма цепи 3-го порядка
Вывод:
В ходе выполнения лабораторной работы были изучены свободные процессы в цепи 1,2,3 порядков. Так, для цепи 1-го порядка процесс является затухающим по экспоненте, обусловленный запасами единственного накопителя. Для цепей 2-го порядка есть 4 вида свободных процессов, различие которых обусловлено видами СЧ, которые определяются параметрами R, L, C элементов. Незатухающий режим, на самом деле затухает, хоть и гораздо медленнее всех остальных процессов. Потери энергии, вероятно, обусловлены внутренним сопротивлением проводов, “неидеальными” компонентами и т. д. В цепях 3-го порядка новых режимов не наблюдается, т. к. он (режим) является совокупностью режимов из цепей 2-го порядка.
Ответы на вопросы
3.2.1 Исследование свободных процессов в цепи 1 порядка
1. Каким аналитическим выражением описывается осциллографируемый процесс?
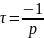U(t)
= A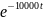
2. Соответствует ли найденная собственная частота теоретическому расчету?
Да, с погрешностью примерно в 9%
3.2.2 Исследование свободных процессов в цепи 2 порядка
3. Какими аналитическими выражениями (в общем виде) описываются процессы во всех четырех случаях?
1)
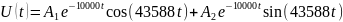
2)
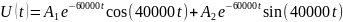
3)
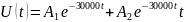
4)
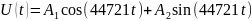
4. Соответствуют ли найденные собственные частоты теоретическому расчету?
Да, с погрешностью не более 10%
5. Каковы теоретические значения собственных частот при 3 кОм и соответствует ли этим значениям снятая осциллограмма?
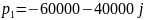
6. Как соотносятся найденные значения добротности с результатами теоретического расчета?
1. В колебательном режиме соответствуют с погрешностью 15%
2. При R = 0 – теоретическое значение стремится к бесконечности, что невозможно в реальной цепи, т.к. сопротивление не может быть равным нулю. Тем не менее, практическое значение добротности равно 32 и существенно больше, чем в других опытах, что соотносится с действительностью.
3.2.3 Исследование свободных процессов в цепи третьего порядка
7. Каким аналитическим выражением описывается осциллографируемый процесс?
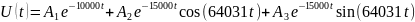
8. Каковы значения собственных частот?
;
15000